带你从入门到精通——机器学习（三. 线性回归）
线性回归是指利用回归方程（函数）对一个或多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式。如果目标值只与一个因变量有关系，称为一元线性回归，形如：y = wx + b。如果目标值与多个自变量都有关系，称为多元线性回归，形式如下：等式最右边是w和x的向量表示。梯度下降法是指沿着梯度下降的方向求解函数的极小值。梯度的本质也是一个向量，在单变量函数中，梯度就是某一点切线斜率（某一点
建议先阅读我之前的博客，掌握一定的机器学习前置知识后再阅读本文，链接如下：
带你从入门到精通——机器学习（一. 机器学习概述）-CSDN博客
带你从入门到精通——机器学习（二. KNN算法）-CSDN博客
目录
二. 线性回归
2.1 线性回归的定义
线性回归是指利用回归方程（函数）对一个或多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式。
如果目标值只与一个因变量有关系，称为一元线性回归，形如：y = wx + b。
如果目标值与多个自变量都有关系，称为多元线性回归，形式如下：
等式最右边是w和x的向量表示。
2.2 线性回归的求解
线性回归的求解过程一般由以下步骤相互配合共同完成：
2.3 损失函数
对于一元线性回归来说，其本质就是想用一条形如y = kx + b的直线去更好的拟合所有样本点，使得误差（误差指预测值y1 – 真实值y2所得到的差值）最小。
那么如何确定最佳的k和b值呢？我们可以引入损失函数来衡量每个样本的预测值和真实值拟合效果，并通过一个优化方法，求损失函数最小值，进而得到k和b的最优解，损失函数也叫代价函数、成本函数、目标函数，它是模型输出（预测值）和观测结果（真实值）之间概率分布差异的量化。
那么该如何设计损失函数呢？对于线性回归模型来说，损失函数一般可以选取以下三种，m为样本的数量：
最小二乘法即求误差平方和，损失函数的具体表达式如下：
平方损失函数即均方误差（Mean Square Error，MSE），损失函数的具体表达式如下：
平均绝对损失函数即平均绝对误差（Mean Absolute Error，MAE），损失函数的具体表达式如下：
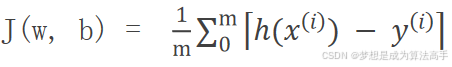
2.4 相关数学知识补充
2.4.1 导数
导数的定义如下：
常见函数的导数如下：
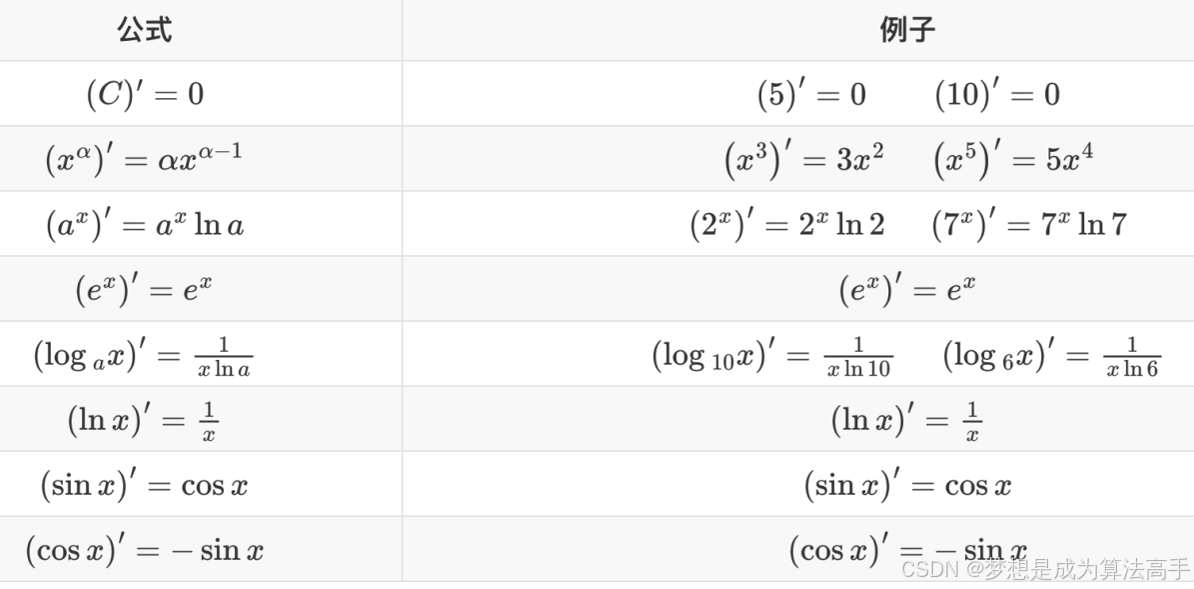
导数的四则运算法则如下：
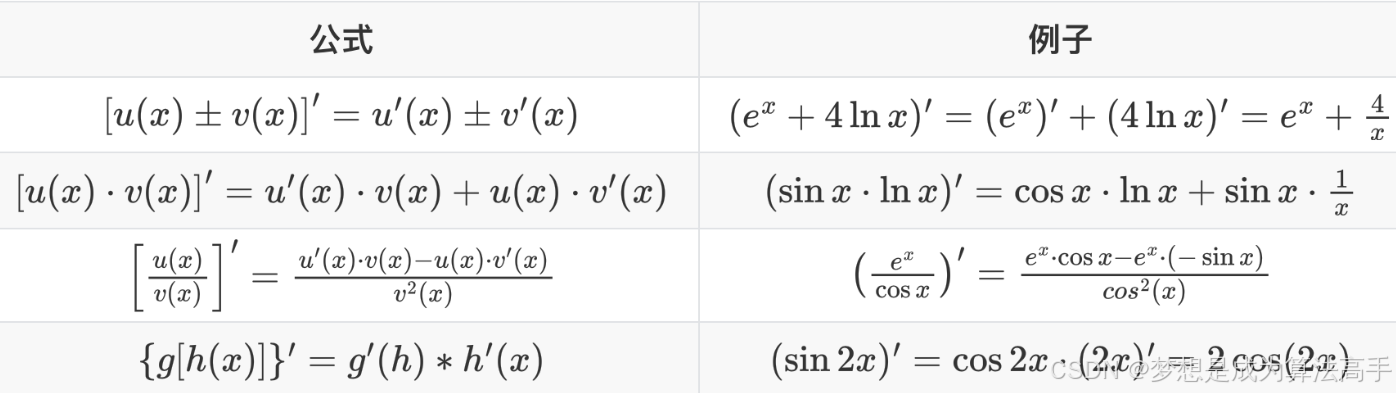
2.4.2 范数
范数（norm）是数学中的一种基本概念，具有长度的意义。
1范数（L1范数）是指向量中各个元素绝对值之和。
2范数（L2范数）即向量的模长，是向量中各个元素平方和的平方根。
p范数是指向量中各个元素p次方和的p次方根。
2.4.3 矩阵
对称方阵是一种特殊的方阵，在行数等于列数的前提下，沿着主对角线（由左上至右下的对角线）的对称位置的元素值相等，即aij = aji，且对称矩阵的转置即为自己本身。
矩阵的求导法则如下：
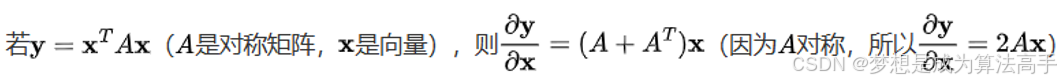
·矩阵的转置法则如下：
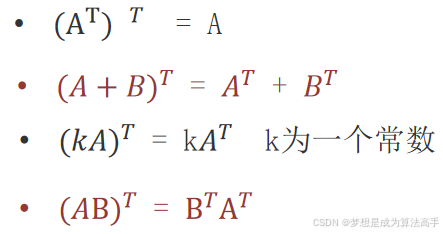
2.5 损失函数优化方法
2.5.1 正规方程法
假设我们有如下的多元线性回归方程式，方程式中x的下标表示x不同的特征维度：
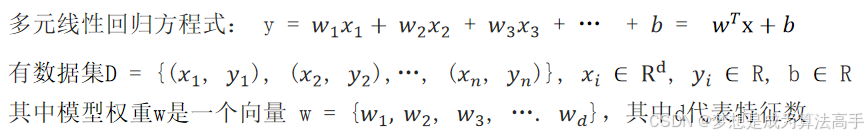
使用最小二乘法可以求得损失函数如下，其中h(x)即为上述的y，这里x的下标表示不同的x样本，m表示样本总数：
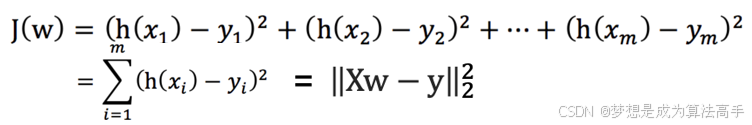
将损失函数展开可以得到如下表达式，注意：
代表一个标量，其转置即为它本身：
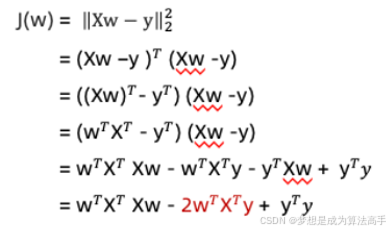
对损失函数求导并令其等于零即可获得w向量的取值，注意：
一定是一个对称矩阵：
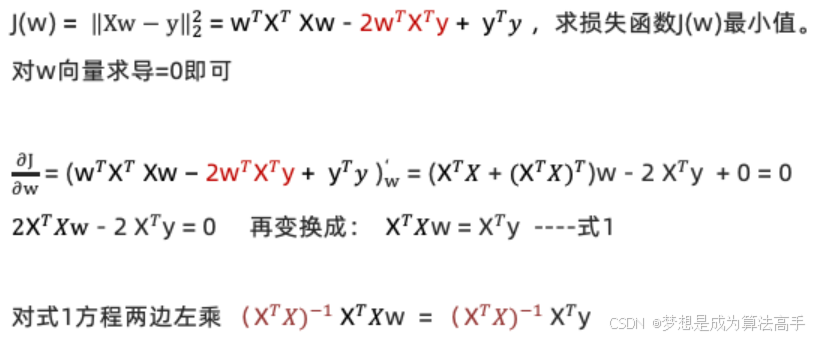
得到最终的结果如下：
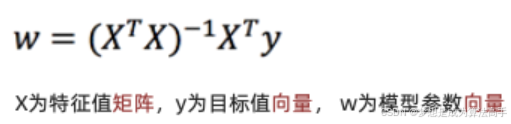
正规方程法的计算量较大，会随着数据维度的增加而增加，且不一定有逆矩阵，如果该矩阵没有逆矩阵，则上述方程无解。
2.5.2 梯度下降法
2.5.2.1 梯度下降法的定义
梯度下降法是指沿着梯度下降的方向求解函数的极小值。
梯度的本质也是一个向量，在单变量函数中，梯度就是某一点切线斜率（某一点的导数），其方向为函数增长最快的方向；在多变量函数中，梯度就是某一个点的偏导数，其方向为偏导数分量的向量方向，将所有变量的偏导数结合起来，即可组成一个多维的梯度向量。
梯度下降法的迭代公式如下：
上式中α表示学习率也称为步长，其取值不能太大，也不能太小，通常建议的取值范围为：0.001 ~ 0.01。
上式中
表示
的梯度，具体计算方式如下：
梯度下降法的优化过程如下：
1. 给定初始位置、步长（学习率），学习率决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度，学习率太小，会导致梯度下降的速度过慢，而学习率太大，则容易造成错过损失函数的最小值、在下降过程中发生震荡、梯度爆炸等问题。
2. 计算该点当前的梯度。
3. 向该梯度的负方向移动相应的步长，因为梯度的方向实际就是函数在此点上升最快的方向，但我们需要朝着下降最快的方向走，即负梯度方向， 所以需要向梯度的负方向移动。
4. 重复2-3步直至算法收敛，收敛的判定条件为：两次迭代的参数变化小于指定的阈值或者达到指定的迭代次数。
2.5.2.2 梯度下降法的分类
梯度下降法主要有以下四种：
全梯度下降算法FGD，指每次迭代时，使用全部样本的平均梯度值进行梯度下降，具体表达式如下，m为样本数量，n为每个样本特征的维度数，注意：可以将系数1/m合并到学习率α中，以简化表达式：
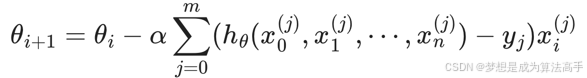
由于FGD使用全部数据集，在训练步相同的情况下，训练速度较慢，并且有可能陷入局部最优解。
随机梯度下降算法SGD，指每次迭代时，随机选择并使用一个样本梯度值进行梯度下降，具体表达式如下：
SGD简单，高效，但不稳定，SGD每次只使用一个样本进行迭代，由于其随机性，使得该算法容易受异常值影响，可能导致在最优解附近波动，不能很好的收敛。
小批量梯度下降算法mini-batch GD，指每次迭代时，随机选择并使用小批量样本的平均梯度值进行梯度下降，即从m个样本中，选择x个样本进行迭代（1<=x<=m），具体表达式如下：
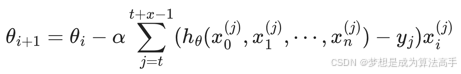
mini-batch GD结合了SGD的胆大和FGD的心细，它的表现也正好居于SGD和FGD二者之间，也是目前使用最多的梯度下降算法，因为它避开了FGD运算效率低、成本大以及SGD收敛效果不稳定的缺点，注意：若batch_size=1，小批量梯度下降算法则变成了SGD，若batch_size=m，小批量梯度下降算法则变成了FGD。
随机平均梯度下降算法SAG，指每次迭代时，随机选择一个样本计算其梯度值，然后和其他样本的历史梯度值取平均值进行梯度下降，具体表达式如下：
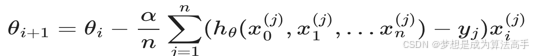
SAG算法的流程如下：
1. 随机选择一个样本，假设选择D样本，计算其梯度值并存储到列表：[D]，然后使用列表中的梯度值的平均值来更新模型参数。
2. 随机再选择一个样本，假设选择G样本，计算其梯度值并存储到列表：[D, G]，然后使用列表中的梯度值的平均值来更新模型参数。
3. 随机再选择一个样本，假设又选择了D样本，重新计算该样本的梯度值，并更新列表中D样本的梯度值，再使用列表中的梯度值的平均值来更新模型参数。
4. 以此类推，直到算法收敛。
由于SAG每轮梯度更新都结合了上一轮梯度值，导致训练初期表现不佳，优化速度较慢。
2.5.3 两种优化方式的对比
两种优化方法的特点对比如下：
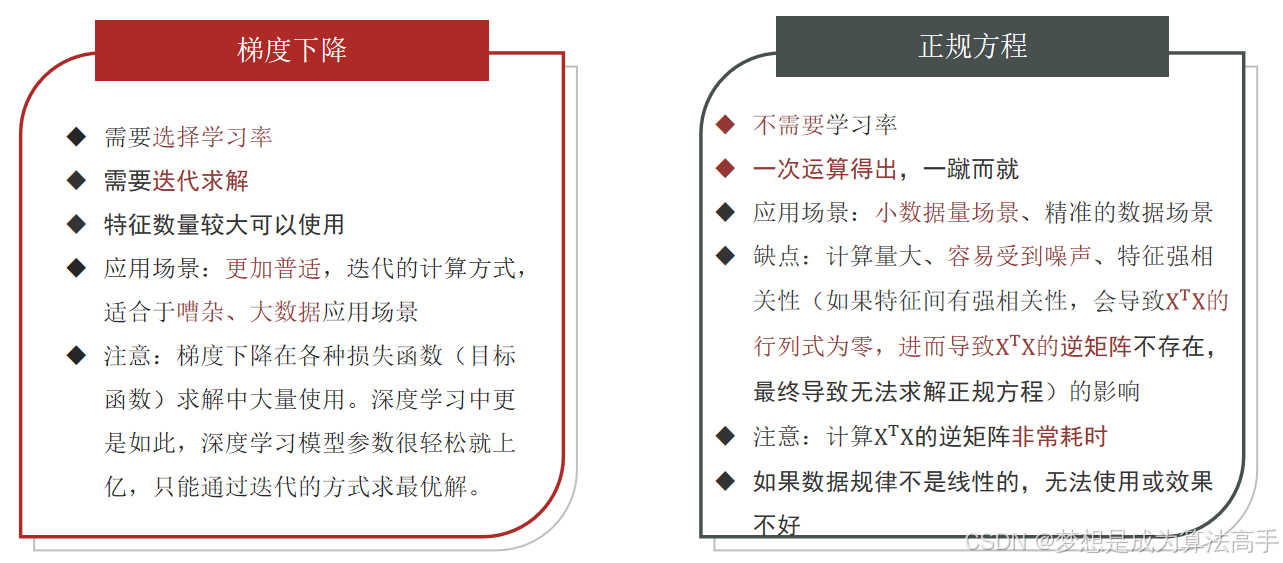
两种优化方法的求解过程对比如下：
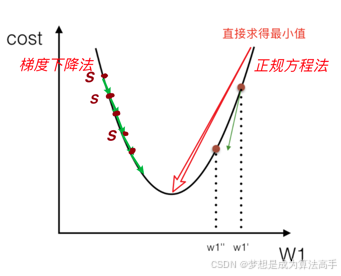
2.6 回归模型的评估方法
回归模型的评估方法可以帮助我们衡量预测值和真实值之间的差距， 常用的评估方法如下：
均方误差（Mean Squared Error，MSE），其具体表达式如下：
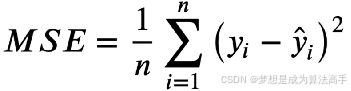
其中n为样本数量, y为实际值, 
为预测值，MSE越小，则表示模型预测越准确。
平均绝对误差（Mean Absolute Error，MAE），其具体表达式如下：
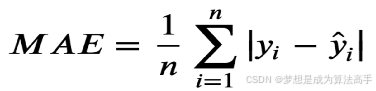
其中n为样本数量, y为实际值, 为预测值，MAE越小，则表示模型预测越准确。
平均绝对百分比误差（Mean Absolute Percentage Error， MAPE）MAPE，其具体表达式如下：
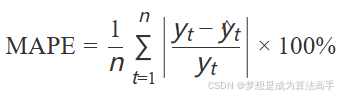
其中n为样本数量, yt为实际值, t为预测值，MAPE越小，则表示模型预测越准确。
均方根误差（Root Mean Squared Error，RMSE），其具体表达式如下：
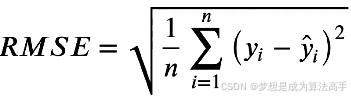
其中n为样本数量, y为实际值, 为预测值，RMSE越小，则表示模型预测越准确，注意RMSE是MSE的平方根。
由于RMSE的计算公式中有一个平方项，因此大的误差将被平方，导致预测误差较大的样本对结果的影响被放大，使得RMSE的值变大，所以RMSE会对异常点更加敏感，而MAE给出的是“真实”的平均误差，对误差大小不敏感。
MAE和RMSE都能反映出预测值和真实值之间的误差，并且大多数情况下RMSE会大于MAE。
可决系数（Coefficient of Determination，R²），也称决定系数，具体表达式如下：
上式中 
表示真实值，
是模型的预测值，
表示真实值的平均值，R²的取值范围是0到1，R²越接近1，表示回归模型拟合得越好，而R²越接近0，表示回归模型拟合得越差。
2.7 过拟合和欠拟合
2.7.1 产生原因
欠拟合是指模型在训练集上表现不好的同时，在测试集上也表现不好，主要原因是模型过于简单，使得模型学习到数据的特征过少。
过拟合是指模型在训练集上表现好，但在测试集上表现不好，主要原因是原始特征过多，且存在一些嘈杂特征，模型尝试去兼顾各个测试数据点，最终使得模型过于复杂。
过拟合和欠拟合与模型复杂度的关系图如下：
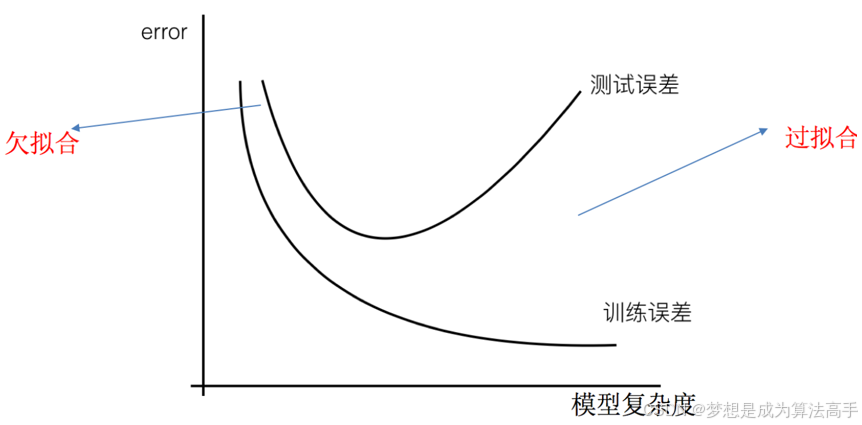
2.7.2 解决方法
欠拟合的解决方法如下：
1. 添加其他特征项：有时出现欠拟合是因为特征项不够导致的，可以通过添加其他特征项，增加特征数量来解决欠拟合。
2. 添加多项式特征：模型过于简单时的常用套路，例如将线性模型通过添加二次项或三次项，以增加模型的复杂度，使模型泛化能力更强。
过拟合的解决方法如下：
1. 重新清洗数据，导致过拟合的一个原因有可能是数据不纯，如果出现了过拟合，可以尝试进行异常值检测并重新清洗数据来解决。
2. 增大数据量，用于训练的数据量太小也会导致过拟合，在增加数据量的情况下，也能够缓解过拟合。
3. 正则化，下一小节会详细介绍
4. 减少特征维度，高维数据通常包含大量特征，过多的特征会导致模型过于复杂，通过降维，可以减少特征数量，同时模型需要估计的参数数量也会减少，能够简化模型结构，降低模型复杂度。
5. 使用早停法（Early stopping），该方法是指当模型训练到某个固定的验证错误率阈值时，及时停止模型训练， 该方法能够防止模型过度训练而出现过拟合。
2.7.3 正则化
在模型训练时，数据提供的特征有些影响模型复杂度或者某些特征的数据异常点较多（异常点数据会造成相应特征的权重系数过大），所以算法在学习的时候尽量减少这个特征的影响（甚至删除这个特征的影响），这就是正则化，我们可以通过损失函数上加上一些限制的方法来实现正则化。
正则化可以控制模型的参数，尤其是高次项的权重参数，进而减少甚至删除某些特征的影响，避免模型过于复杂，缓解过拟合的影响。
正则化的方式分为L1正则化和L2正则化：
L1正则化，指在损失函数中添加L1正则化项，损失函数的表达式如下：
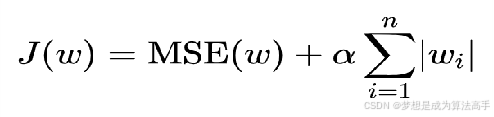
其中α叫做惩罚系数，该值越大则权重调整的幅度就越大，即对特征权重的惩罚力度就越大，所得模型的权重系数就越小。
L1正则化会使得权重趋向于0，甚至等于0，使得某些特征失效，达到特征筛选的目的，通常使用L1正则化的模型是一个稀疏模型，L1正则也可以在一定程度上防止模型过拟合。
注意：使用L1正则化的线性回归模型被称为Lasso回归。
L2正则化，指在损失函数中添加L2正则化项，损失函数的表达式如下：
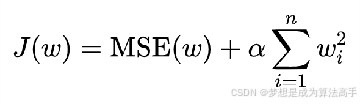
α也为惩罚系数，L2 正则化会使得权重趋向于0，但一般不等于 0，L2正则化能够让模型产生一些平滑的权重系数，在实际工程中一般倾向使用L2正则化
注意：使用L2正则化的线性回归模型被称为岭回归（Ridge Regression）。
2.8 波士顿房价预测项目
使用线性回归模型完成波士顿房价预测项目的具体实现代码如下：
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Lasso, Ridge
from sklearn.metrics import mean_squared_error, mean_absolute_error
# 加载数据
data = pd.read_csv('波士顿房价xy.csv')
print(data.info())
# 划分特征和标签
X = data.iloc[:, :-1]
y = data.iloc[:, -1]
# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=66)
# 特征预处理：标准化
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
lr = LinearRegression() # 创建线性回归模型，该模型使用正规方程法优化模型
sgd = SGDRegressor() # 创建线性回归模型，该模型使用随机梯度下降法优化模型
lasso = Lasso() # 创建Lasso回归模型
ridge = Ridge() # 创建Ridge回归模型
# 模型训练
lr.fit(x_train, y_train)
sgd.fit(x_train, y_train)
lasso.fit(x_train, y_train)
ridge.fit(x_train, y_train)
# 模型预测
y_pred_lr = lr.predict(x_test)
y_pred_sgd = sgd.predict(x_test)
y_pred_lasso = lasso.predict(x_test)
y_pred_ridge = ridge.predict(x_test)
# 模型评估
print(f'lr的MAE:{mean_absolute_error(y_test, y_pred_lr)}')
print(f'lr的MSE:{mean_squared_error(y_test, y_pred_lr)}')
print(f'sgd的MAE:{mean_absolute_error(y_test, y_pred_sgd)}')
print(f'sgd的MSE:{mean_squared_error(y_test, y_pred_sgd)}')
print(f'lasso的MAE:{mean_absolute_error(y_test, y_pred_lasso)}')
print(f'lasso的MSE:{mean_squared_error(y_test, y_pred_lasso)}')
print(f'ridge的MAE:{mean_absolute_error(y_test, y_pred_ridge)}')
print(f'ridge的MSE:{mean_squared_error(y_test, y_pred_ridge)}')
'''
输出结果如下：
lr的MAE:2.976387505351346
lr的MSE:15.786404126744863
sgd的MAE:2.9222650310685934
sgd的MSE:15.768503047427034
lasso的MAE:3.465966724545685
lasso的MSE:23.168208059533196
ridge的MAE:2.9648663699002142
ridge的MSE:15.748746707576785
'''
技术共进，成长同行——讯飞AI开发者社区
更多推荐
39
0- 0
已为社区贡献16条内容
所有评论(0)