Python大本营连载栏目更新啦！

本期，邀请到了清华大学硕士张雨萌老师。

当下机器学习、人工智能领域吸引了许多技术人才投身其中，数学知识繁杂的理论与思想方法是大家在学习过程中的难点，这篇专栏将机器学习涉及到的数学知识统一梳理出来，相信你可以有所收获。

今天，由张雨萌老师为大家分享其原创专栏《机器学习中的数学》中《机器学习概率统计》第一篇：从概率到条件概率。

从今天开始，张老师将连续 7 天为大家分享其原创专栏《机器学习中的数学》中的内容。

看到最后别忘了给老师打call，滑到文章底部分享、点赞、再看哦！

第一天分享内容：从概率到条件概率

首先你需要知道：

机器学习里，数学为什么很重要？

在当下，机器学习、人工智能领域吸引了许多同学投身其中，其中包含了大量非科班出身或者从其他行业切换赛道转行而来的朋友们，大家在学习的过程中发现学习曲线陡峭、难度较大，普遍的心声就是：机器学习难，首要就是数学知识需要的太多了！

的确如此，机器学习是一个综合性强、知识栈长的学科，需要大量的前序知识作为铺垫，最核心、最基础的就是他的绝大多数算法模型和实际应用都依赖于以概率统计、线性代数和微积分为代表的数学理论和思想方法。

比方说吧：

• 想进行语音识别？隐马尔可夫模型你不可不会；想对一句话进行词性标注？条件随机场你敢不懂？

• 在进行贝叶斯推断的时候，如果对马尔科夫链蒙特卡洛方法等近似推断一无所知，可能一个复杂的概率分布就让你举步维艰；

• 对时间序列进行预测，或许卡尔曼滤波、粒子滤波对你来说是一个好的选择；

• 进行样本分类、聚类这些常规操作时，逻辑回归、高斯判别、高斯混合等各种模型都应该如数家珍；

因此，可以看出，数学基础是机器学习绕不开的一块阵地。

‍‍从这一节开始，我们就正式进入到概率统计的内容板块中了。

一、条件概率的发生背景

对于概率，相信大家都不会陌生，在各阶段的数学课上，他都是高频出现的常客，最简单的概率场景比如掷骰子，我问你：第一次掷出的点数为 5 的概率为多大？你会毫不犹豫的说出答案：1/6。

这太简单了，如果我们只满足于此，就没有什么意义了。接下来我增加一个限定条件：已知在抛出骰子是奇数的情况下，抛掷点数为 5 的可能性有多大？

发现了没有，在第二个问题中我们就没有直接的只问投掷出 5 这个事件的概率，而是增加了一个前提条件：这次抛掷出的点数为奇数。

生活中这类场景更多，我们一般不会直接去推断一个事件发生的可能性，因为这样实际意义并不明显，而且也不容易推断出结果，比如我们问你今天下雨的概率是多大？你可能是一头雾水，什么地点？什么月份？当日云层的厚度？这些条件都没有告诉，我想是无法给出一个有意义、有价值的合理推断的。

而且在实际情况下，一个事件一般而言也不会是孤立的发生，也都会伴随着其他的一些事情或表现一同出现，单独的谈一个事件的概率，一般而言也是不存在的。

因此，在实际的应用中，我们更关心的是条件概率，也就是在给定部分信息的基础上对试验结果的推断。这些给定的信息就是我们附加的条件，是我们研究时关注的重点。

二、条件概率的具体描述

这里，我们来具体描述一下条件概率：

假设我们知道给定事件 B 已经发生，在此基础上希望知道另一个事件 A 发生的可能性，此时我们就需要构造出条件概率，它需要先顾及事件 B 已经发生的信息，然后再求出事件 A 发生的概率。

这个条件概率描述的就是在给定事件BB发生的情况下，事件 A 发生的概率，我们专门把他记作：P(A|B) 。

那我们回到投掷骰子的问题中来，在投出奇数点数骰子的前提下，投出 5 的概率有多大？奇数点数一共有 {1,3,5} 三种，其中出现 5 的概率是 1/3。很明显，和单独问投出点数是 5 的概率计算结果是不同的。

下面我们来抽象一下条件概率的场景。

我们再回到最简单、最容易理解的情景下来看，即在古典概率的模式下来分析：假定一个试验有 N 个等可能的结果，事件 A 和 B 分别包含 M1 个和  M2 个结果，这其中 M12 个结果是公共的，这就是同时发生事件 A 和事件 B，即 A∩B 事件所包含的试验结果数。

形象的描述一下上述场景，如图所示：‍‍

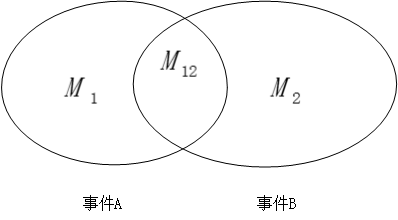
‍‍‍‍‍‍那我问你，单纯的发生事件 A 和事件 B 的概率是多少？你肯定是脱口而出，分别是

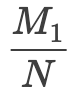和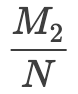，那进一步到条件概率中来，已知在事件BB发生的前提条件下，事件 A 发生的概率是多少？

则此时，我们的整体考虑范围由最开始的NN个全部的可能结果局限到现在的 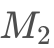 个结果，即 B 事件发生的结果范围，而这其中只有  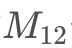个结果对应事件AA的发生，那么我们不难计算出，条件概率  。

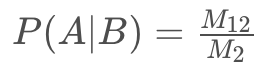三、条件概率的表达式分析

‍‍‍‍‍‍‍‍为了更加深入的挖掘这里面的内涵，我们进一步的对条件概率的表达式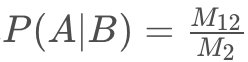进行展开：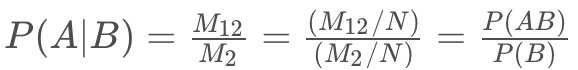

由此，我们得到了条件概率的一般定义：。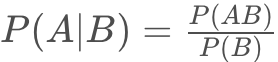

‍‍‍‍‍‍‍‍‍‍好了，本次分享的内容就到这里，感觉有收获的同学，可以滑到文章底部，帮助老师分享点赞收藏，咱们明天见！

下期预告：两个事件的独立性、从条件概率到全概率公式、聚焦贝叶斯公式。

注：以上内容及后续将要连续分享的内容，均来自张雨萌老师在CSDN专栏创作的《机器学习中的数学》。

‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

扫码下方二维码，

查看张老师更多的专栏内容

学习了解张老师的专栏内容