机器学习实战——逻辑回归和线性判别分析
逻辑回归函数原型为sklearn.linear_model.LogisticRegression(...)参数penalty:一个字符串,指定了正则化策略l2 优化目标函数为12∣∣ω∣∣22+CL(ω),C>0,L(ω)\frac{1}{2}||\pmb{\omega}||_2^2 +CL(\pmb \omega),C>0,L(\pmb \omega...
逻辑回归
函数原型为
sklearn.linear_model.LogisticRegression(...)
参数
-
penalty:一个字符串,指定了正则化策略
- l2 优化目标函数为12∣∣ω∣∣22+CL(ω),C>0,L(ω)\frac{1}{2}||\pmb{\omega}||_2^2 +CL(\pmb \omega),C>0,L(\pmb \omega)21∣∣ωωω∣∣22+CL(ωωω),C>0,L(ωωω)为极大似然函数
- l1 优化目标函数为∣∣ω∣∣1+CL(ω)||\pmb \omega ||_1 +CL(\pmb \omega)∣∣ωωω∣∣1+CL(ωωω)
-
dual:是否求解对偶形式
-
C:一个浮点数,表示惩罚项系数的倒数,越小表示正则项越大
-
fit_intercept:是否计算b值
-
intercept_scaling:一个浮点数,只有当solver=‘liblinear’才有意义
-
class_weight:一个字典或者字符串‘balanced’
- 如果为字典,则字典给每个分类的权值
- 如果为balanced, 则每个分类的权重与该分类在样本集中出现的频率成反比
- 如果没有指定,则权重为1
-
solver:一个字符串,指定了求解最优化问题的算法
-
newton-cg 使用牛顿法
-
lbfgs 使用L-BFGS拟牛顿法
-
liblinear 使用liblinear
-
sag 使用Stochastic Average Gradient descent算法
注意:
-
对于规模较小的数据集,liblinear比较合适,对于较大的数据集,sag比较合适
-
其余的只处理penalty=‘l2’的情况
-
-
multi_class:一个字符串,指定对分类问题的策略
- ovr 采用one-vs-rest策略
- multinomial 直接采用多分类逻辑回归策略
-
verbose 一个证书3,用于开启/关闭迭代中间输出日志功能
方法
- predict_log_proba(X) 返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值
- predict_porba(X) 返回一个数组,数组的元素依次是X预测为各个类别的概率值
选用的数据集为鸢尾花数据一共有150数据,这些数据分为3类(setosa,versicolor,virginica),每类50个数据,每个数据包含4个属性:萼片(sepal)长度,萼片宽度,花瓣(petal)长度,花瓣宽度。
导入数据
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, discriminant_analysis, model_selection
def load_data():
iris = datasets.load_iris()
X_train = iris.data
y_train = iris.target
return model_selection.train_test_split(X_train,y_train,test_size=0.25,random_state=0,stratify=y_train)
调用LogisticRegression函数
def test_LogisticRegression(*data):
X_train,X_test, y_train, y_test = data
regr = linear_model.LogisticRegression()
regr.fit(X_train,y_train)
print("Coefficients:%s\n intercept %s"%(regr.coef_, regr.intercept_))
print("Score: %.2f" %(regr.score(X_test,y_test)))
结果
Coefficients:[[ 0.38705175 1.35839989 -2.12059692 -0.95444452]
[ 0.23787852 -1.36235758 0.5982662 -1.26506299]
[-1.50915807 -1.29436243 2.14148142 2.29611791]]
intercept [ 0.23950369 1.14559506 -1.0941717 ]
Score: 0.97
多分类参数对分类结果的影响,默认的采用的是one-vs-rest策略,但是回归模型原生就支持多分类。
def test_LogisticRegression_multinomial(*data):
X_train,X_test, y_train, y_test = data
regr = linear_model.LogisticRegression(multi_class='multinomial', solver='lbfgs')
regr.fit(X_train,y_train)
print("Coefficients:%s\n intercept %s"%(regr.coef_, regr.intercept_))
print("Score: %.2f" %(regr.score(X_test,y_test)))
牛顿法或拟牛顿法才能配合multi_class=‘multinomial’,否则报错
结果
Coefficients:[[-0.38340846 0.86187824 -2.27003634 -0.9744431 ]
[ 0.34360292 -0.37876116 -0.03099424 -0.86880637]
[ 0.03980554 -0.48311708 2.30103059 1.84324947]]
intercept [ 8.75830949 2.49431233 -11.25262182]
Score: 1.00
准确率达到了100%
最后看C对分类模型预测性能的影响
def test_LogisticRegression_C(*data):
X_train,X_test, y_train, y_test = data
Cs = np.logspace(-2,4,num=100)
scores = []
for C in Cs:
regr = linear_model.LogisticRegression(C=C)
regr.fit(X_train,y_train)
scores.append(regr.score(X_test,y_test))
# 绘图
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(Cs,scores)
ax.set_xlabel(r"C")
ax.set_ylabel(r"score")
ax.set_xscale("log")
ax.set_title("LogisticRegression")
plt.show()
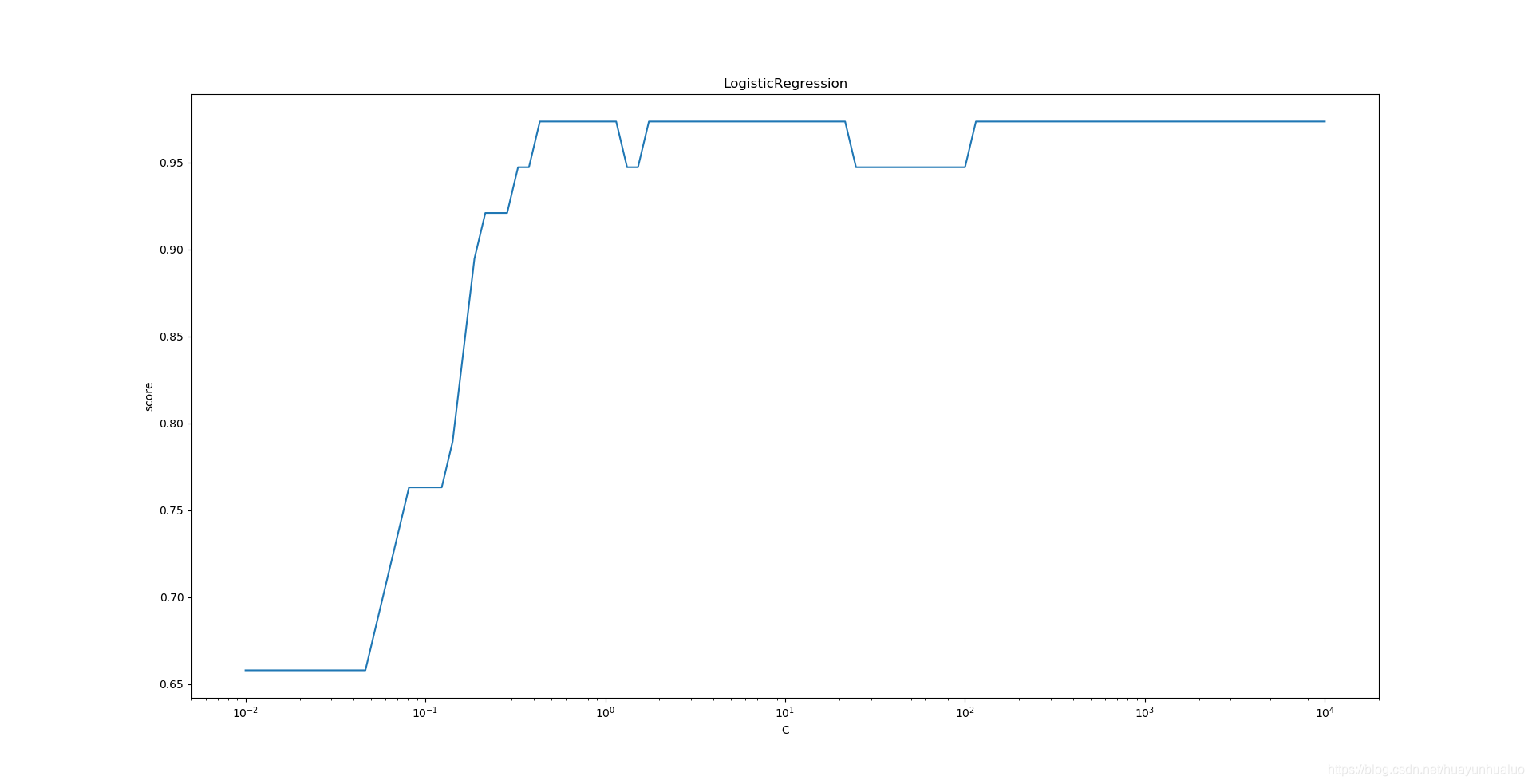
随着C的增大,预测的准确率在上升,在一定的程度,预测维持在较高的水准保持不变
线性判别分析
函数原型
class sklearn.discriminant_analysis.LinearDiscriminantAnalysis()
参数
- solver 一个字符串,指定求解最优化问题的算法
- svd 奇异值分解,对于大规模特征的数据,推荐使用这种算法
- lsqr 最小平方差算法,可以结合skrinkage参数
- eigen 特征值分解算法 可以结合skrinkage参数
- skrinkage 字符串‘auto’或浮点数或None,该参数通常在训练样本数量小于特征数量的场合下使用
- auto 根据Ledoit-Wolf 引理来自动决定skrinkage参数大小
- None 不使用skrinkage参数
- 浮点数 指定skrinkage 参数
- priors 一个数组,数组中元素依次制定了每个类别的先验概率,如果为None,则每个类的先验概率是相同的
- n_components 降维后的维度
- store_covariance 一个布尔值,表示是否需要额外计算每个类别的协方差矩阵
属性:
- covariance : 一个数组,依次给出每个类别的协方差矩阵
- means_ 依次给出每个类别的均值向量
- xbar_ 给出了整体样本的均值向量
def test_LinearDiscriminantAnalysis(*data):
X_train,X_test, y_train, y_test = data
lda = discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X_train,y_train)
print("Coefficients:%s\n intercept %s"%(lda.coef_, lda.intercept_))
print("Score: %.2f" %(lda.score(X_test,y_test)))
结果是
Coefficients:[[ 6.66775427 9.63817442 -14.4828516 -20.9501241 ]
[ -2.00416487 -3.51569814 4.27687513 2.44146469]
[ -4.54086336 -5.96135848 9.93739814 18.02158943]]
intercept [-15.46769144 0.60345075 -30.41543234]
Score: 1.00
预测准确率为1.00 说明LinearDiscriminantAnalysis()对于测试集完全正确。
现在可视化一下降维后的数据集
def plot_LDA(converted_X,y):
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
colors = 'rgb'
markers = 'o*s'
for target , color,marker in zip([0,1,2],colors,markers):
pos = (y==target).ravel()
X=converted_X[pos,:]
ax.scatter(X[:,0],X[:,1],X[:,2],color=color,marker = marker, label="Label %d"%target)
ax.legend(loc="best")
fig.suptitle("Iris After LDA")
plt.show()
X_train ,X_test,y_train,y_test = load_data()
X = np.vstack((X_train,X_test))
Y = np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))
lda = discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X,Y)
converted_X = np.dot(X,np.transpose(lda.coef_))+lda.intercept_
plot_LDA(converted_X,Y)
结果如下
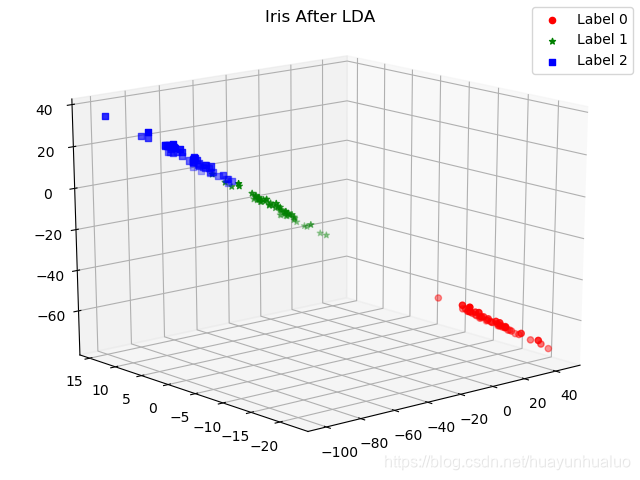
接下来看不同的solver对预测性能的影响
def test_LinearDiscriminantAnalysis_solver(*data):
X_train,X_test, y_train, y_test = data
solvers = ['svd','lsqr','eigen']
for solver in solvers:
if (solver == 'svd'):
lda = discriminant_analysis.LinearDiscriminantAnalysis(solver=solver)
else :
lds = discriminant_analysis.LinearDiscriminantAnalysis(solver=solver, shrinkage=None)
lda.fit(X_train,y_train)
print("Score at solver=%s: %.2f"%(solver, lda.score(X_test,y_test)))
结果
Score at solver=svd: 1.00
Score at solver=lsqr: 1.00
Score at solver=eigen: 1.00
最后考察在solver=lsqr,引入抖动相当于引入正则化项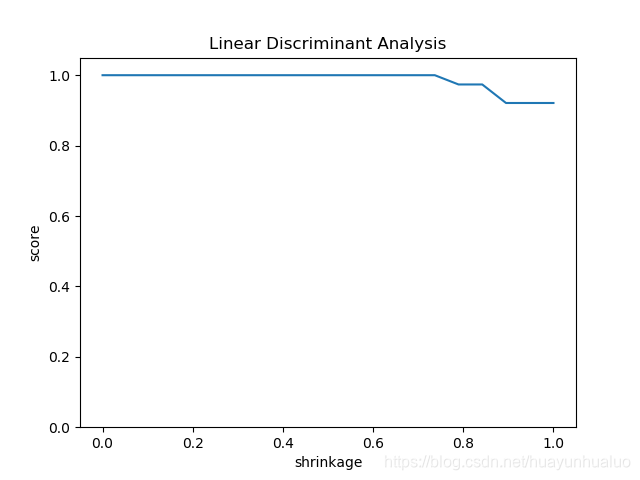
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容









所有评论(0)