假设权重都被初始化为0或者非0，那么第二层的每个隐藏单元都会有相同的值，这导致dw^([l])=dz^([l])⋅a^([l-1])（不懂可以参考该篇——反向传播）是相同的，使得梯度下降更新中的梯度会保持相等，权重相同，即使进行了梯度更新，但隐藏单元仍以相同的函数作为输入，导致计算不出其他的函数，即隐藏单元是对称的，这种情况下超过1个隐藏单元也没有什么意义，因为他们计算的是相同的东西，为了打破这种对称性，需要进行随机初始化。

所以应该这么做：把W^([1])设为np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如0.01，这样把它初始化为很小的随机数。b 初始化为0

为什么需要乘一个很小的数，如果w很大，那么很可能最终停在（甚至在训练刚刚开始的时候）z很大的值，这会造成tanh/Sigmoid激活函数饱和在龟速的学习上，如果没有sigmoid/tanh激活函数在你整个的神经网络里，就不成问题。这对浅层的神经网络这样做还可以，但是对于深层的神经网络，这样做还是不够的。

对于深层的神经网络需要去控制梯度消失和梯度爆炸问题，当初始化的网络权值小于1时，这会导致层数增多时，小于1的值不断相乘，最后导致激活项很小。当权值大于1时，大于1的值不断相乘，最后导致激活项很大。计算梯度时，利用如下的两个公式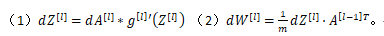

如果激活函数选择Sigmoid，当Z^([l])远大于1时，g^[l]’(Z^([l]))小于1，当层数增多时梯度是以指数形式递减的，最终造成梯度消失，而当Z^([l])接近较小时，g^[l]’(Z^([l]))大于1，当层数增多时梯度是以指数形式递增的最终会导致梯度爆炸。对于该问题的解决办法：对于sigmoid和tanh函数：设置某层初始化权重矩阵为w^([l])=np.random.randn(shape)*np.sqrt(1/n^([l-1]))，n^([l-1])就是第l-1层神经元数量,即最后一个隐藏层。对于relu激活函数通常会乘np.sqrt(2/n^[l-1] )。