机器学习之基础总结

1. 先验概率和后验概率先验概率（prior probability）：字面意思，实验之前的概率，也即根据以往经验和分析（事先可估计）得到概率。后验概率（posterior probability）：字面意思，实验之后的概率，换句话说，某个因素引起事件发生的概率。全概率公式贝叶斯公式参考资料全概率公式、贝叶斯公式...

jiet07

239人浏览 · 2021-04-13 23:11:35

jiet07 · 2021-04-13 23:11:35 发布

1. 先验概率和后验概率

先验概率（prior probability）：字面意思，实验之前的概率，也即根据以往经验和分析（事先可估计）得到概率。

后验概率（posterior probability）：字面意思，实验之后的概率，换句话说，某个因素引起事件发生的概率。

先验概率，后验概率与全概率公式和贝叶斯公式的联系

全概率公式
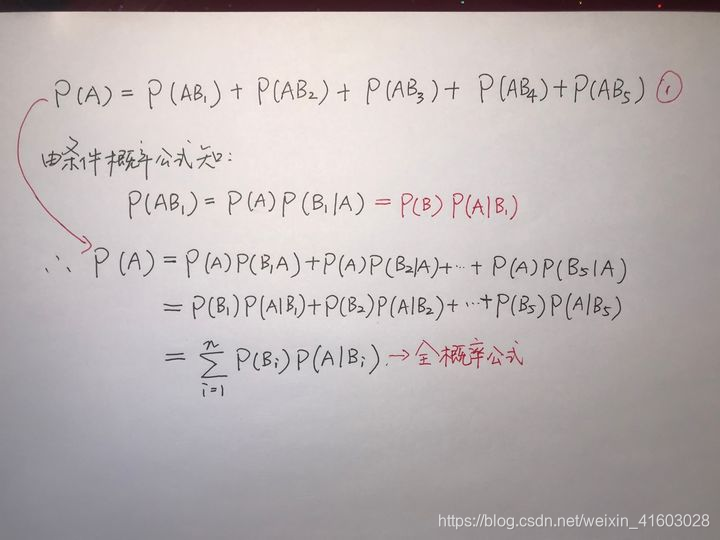
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

全概率公式的意义

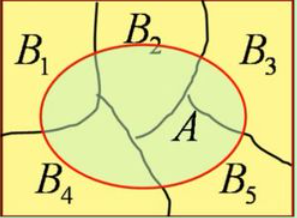
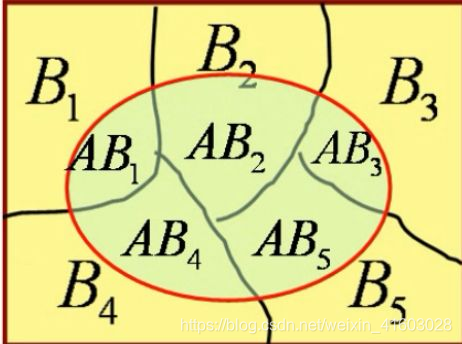
综上可知，将复杂的事件A划分成简单的事件 $AB_1，AB_2,......,AB_n$ ，再结合加法公式和乘法公式计算出A的概率。

换句话说，事件A的发生有各种可能的原因 $B_i(i=1,...,n)$ 。如果A是由原因 $B_i$ 引起，则A发生的概率为 $P(AB_i)=P(B_i)P(A|B_i)$ 。每一个原因都可能导致A发生，故A发生的概率是全部原因引起A发生的概率的总和，即为全概率公式。

由此可以形象地把全概率公式看成是“由原因推结果”，也即由因推果。当知道某件事的原因后，推断由某个原因导致这件事发生的概率为多少。（如果A是由原因 $B_i$ 引起，则A发生的概率为 $P(AB_i)=P(B_i)P(A|B_i)$ ）

贝叶斯公式

参考资料

全概率公式、贝叶斯公式

技术共进，成长同行——讯飞AI开发者社区

更多推荐

论文笔记：AlphaEdit: Null-Space Constrained Knowledge Editing for Language Models（AlphaEdit）

论文发表于人工智能顶会ICLR（基于定位和修改的模型编辑方法（针对和等）会破坏LLM中最初保存的知识，特别是在顺序编辑场景。为此，本文提出AlphaEdit：1、在将保留知识应用于参数之前，将扰动投影到保留知识的零空间上。2、从理论上证明，这种预测确保了在查询保留的知识时，编辑后的LLM的输出保持不变，从而减轻中断问题。3、对各种LLM（包括LLaMA3、GPT2XL和GPT-J）的广泛实验表明，