神经网络算法是如何提取到更多有用的信息，从而实现更加精准的映射？下面通过异或的实现来展现神经网络的强大之处（激活函数为sigmoid函数）。
对于sigmoid激活函数而言，该函数图像如下，g(4.6)约等于1，g(-4.6)约等于0.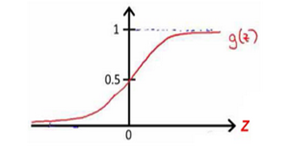

下图的神经元（三个权重分别为-30，20，20）可以被视为作用同于逻辑与（AND）：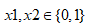


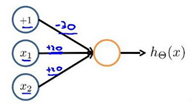
下图的神经元（三个权重分别为-10，20，20）可以被视为作用等同于逻辑或（OR），分析与逻辑与的过程相同，便不再赘述：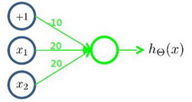

下图的神经元（两个权重分别为 10，-20）可以被视为作用等同于逻辑非（NOT）：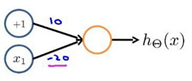

我们可以利用神经元来组合成更为复杂的神经网络以实现更复杂的运算。例如我们要实现XNOR(同或) 功能（输入的两个值必须一样，均为1或均为0），即：
$$XNOR=(x_{1}AND{x}_2)OR((NOT{x}_1)AND(NOT{x}_2))$$
首先构造一个能表达(NOT x_1 )AND(NOT x_2 )部分的神经元：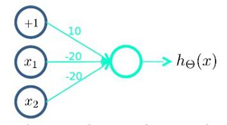

然后将表示 AND 的神经元和表示 $(NOT{x}_1)AND(NOT{x}_2)$ 的神经元以及表示 OR 的神经元进行组合：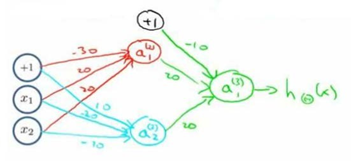

我们就得到了一个能实现 XNOR 运算符功能的神经网络。
对于XOR(异或)，采用的方法与上面的一样:
$$XOR=(x_{1}OR{x}_2)AND((NOT{x}_1)OR(NOT{x}_2))$$按这种方法我们可以逐渐构造出越来越复杂的函数，也能得到更加厉害的特征值。因此神经网络可以提取到更多的特征，进行更好的拟合。
另外经过异或的实现，可以看出这里有三层结构才将异或实现，因此也从侧面证明了单层感知器没办法实现异或功能。