详解卷积神经网络中的多输入多输出通道
定义输入数据包含多个通道(例如彩色图像的 RGB 三通道)。每个通道有独立的卷积核集合,分别处理不同通道的信息。定义每个卷积层生成多个输出通道(也称为 “特征图”)。每个输出通道对应一组独立的卷积核,提取不同类型的特征。
目录
详解sum(d2l.corr2d(x, k) for x, k in zip(X, K))?
详解torch.stack([corr2d_multi_in(X, k) for k in K], 0)?
1. 列表推导式:[corr2d_multi_in(X, k) for k in K]
2. torch.stack(..., 0):在第 0 维度堆叠
什么是多输入通道?
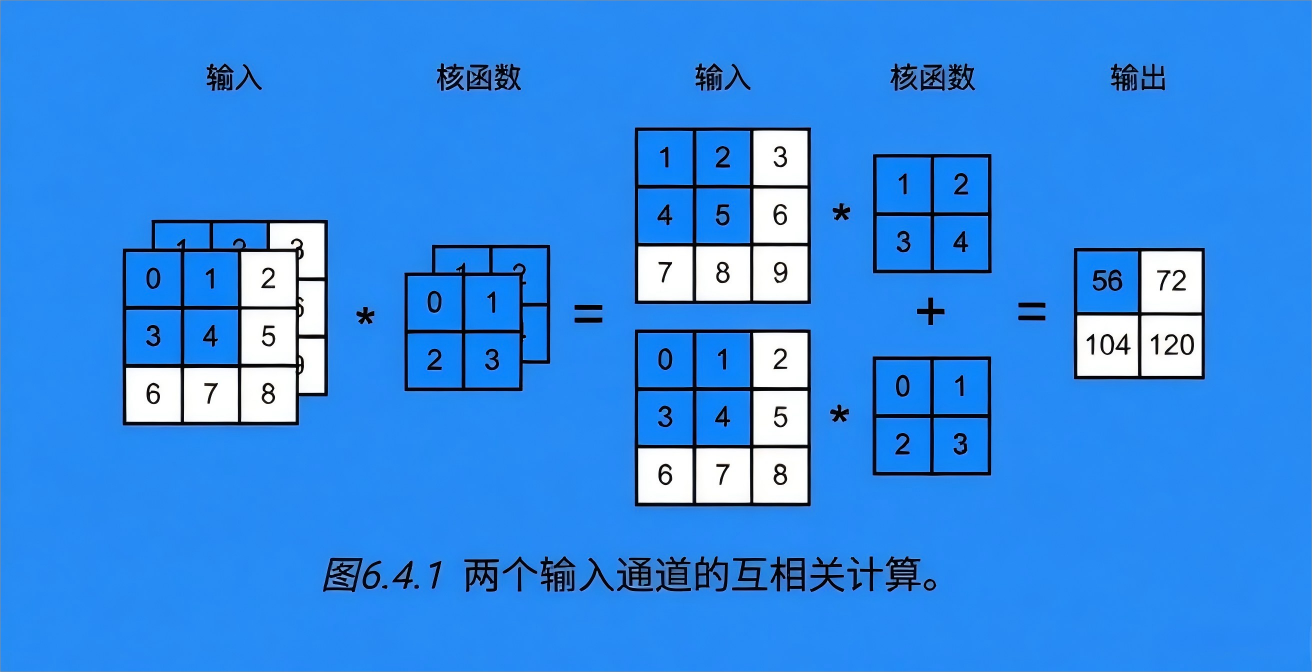
1. 定义
- 输入数据包含多个通道(例如彩色图像的 RGB 三通道)。
- 每个通道有独立的卷积核集合,分别处理不同通道的信息。
2. 功能与作用
- 融合多源信息: 例如彩色图像的 RGB 通道分别携带不同颜色信息,多输入通道允许模型同时处理这些信息,提取更丰富的特征。
- 参数共享的扩展: 每个通道的卷积核参数不同,但同一通道的卷积核在整个输入上共享参数,大幅减少参数量。
3. 数学原理
假设输入为
个通道,卷积核尺寸为
,则:
- 每个输出通道需要
个
的卷积核(每个输入通道对应一个)。
- 所有卷积核的输出按元素相加,形成单个输出通道。
什么是多输出通道?
1. 定义
- 每个卷积层生成多个输出通道(也称为 “特征图”)。
- 每个输出通道对应一组独立的卷积核,提取不同类型的特征。
2. 功能与作用
- 特征多样化: 不同输出通道可以学习不同类型的特征(例如边缘、纹理、颜色等),使模型具备更全面的感知能力。
- 层次化特征提取: 深层网络通过堆叠多输出通道的卷积层,逐步提取从低级到高级的语义特征(如从边缘到物体部件再到完整物体)。
3. 数学原理
- 若设置
个输出通道,则需要
组卷积核(每组包含
个卷积核)。
- 每组卷积核生成一个独立的输出通道。
相比单通道而言,多通道的优劣势?
维度 多通道 单通道 优势 高表达能力、参数效率、适合复杂任务 低计算开销、简单易用 劣势 高计算复杂度、训练难度大 信息损失、扩展性差 核心价值 深度提取多维特征 快速处理简单任务 一、多通道(多输入 / 多输出)的优势
1. 表达能力更强
多输入通道: 能同时处理多维数据(如 RGB 三通道图像),融合不同维度的信息,提取更丰富的特征。
示例:彩色图像的 R、G、B 通道分别携带不同颜色信息,多通道可同时利用这些信息,而单通道需手动合并或丢弃部分信息。
多输出通道: 每个输出通道可学习不同类型的特征(如边缘、纹理、颜色),使模型具备更全面的感知能力。
对比:单输出通道只能提取单一类型的特征,无法同时捕获多种模式。
2. 参数效率更高
- 参数共享: 多通道卷积通过参数共享大幅减少参数量。例如,处理 3 通道输入时,每个输出通道只需 3 个卷积核(而非为每个位置单独设计参数)。
- 数据:对于 5×5 卷积核,单通道需 25 个参数,而 3 输入通道、8 输出通道的卷积层仅需
个参数(远少于单通道逐一处理的参数量)。
3. 适合复杂任务
多模态融合: 多输入通道天然支持处理多模态数据(如图像 + 音频),而单通道需复杂的预处理。
应用:自动驾驶中同时处理摄像头(RGB)和雷达(深度信息)。
层次化特征提取: 多输出通道通过堆叠卷积层,可逐步提取从低级到高级的语义特征(如从边缘到物体部件),适合复杂分类、检测任务。
二、多通道的劣势
1. 计算复杂度更高
- 内存占用: 多通道卷积需要存储更多卷积核和中间结果。例如,8 输出通道的卷积层比单输出通道多占用 8 倍显存。
- 优化:通过分组卷积(Grouped Convolution)或深度可分离卷积(Depthwise Separable Convolution)降低计算量。
2. 训练难度更大
- 梯度消失 / 爆炸: 通道数过多可能导致梯度在反向传播中不稳定,需要更复杂的优化策略(如 Batch Normalization、残差连接)。
3. 过拟合风险
- 若数据量不足,多通道模型可能因参数过多而陷入过拟合。 应对:增加数据增强、正则化(L1/L2)或 Dropout。
三、单通道的优势
1. 简单高效
- 低计算开销: 单通道卷积计算简单,适合资源受限的场景(如嵌入式设备、实时应用)。
- 示例:早期手机端图像滤镜(如黑白滤镜)只需单通道处理。
2. 适合简单任务
- 对于结构简单、特征单一的任务(如边缘检测),单通道模型可能已足够,无需引入多通道的复杂性。
四、单通道的劣势
1. 信息损失严重
- 无法同时处理多维信息,需手动设计特征组合。例如,单通道处理彩色图像时,需先将 RGB 合并为灰度图,导致颜色信息丢失。
2. 扩展性差
- 难以应对复杂任务(如语义分割、多目标检测),因为单通道无法并行提取多样化特征。
不同通道的应用场景?
场景 多通道 单通道 输入数据类型 多维数据(如 RGB 图像、多传感器数据) 一维或单一模态数据(如灰度图) 任务复杂度 高(分类、检测、分割) 低(简单滤波、边缘检测) 计算资源 充足(GPU/TPU) 受限(嵌入式设备) 数据量 大 小 典型应用 现代 CNN(ResNet、YOLO) 传统图像处理(OpenCV 滤镜)
详解sum(d2l.corr2d(x, k) for x, k in zip(X, K))?
一、功能概述
这行代码实现了多输入通道的二维互相关运算,其核心逻辑是:
- 分组计算:将输入张量
X和卷积核K按通道维度(第 0 维)一一配对。- 单通道运算:对每对通道执行单通道互相关运算(调用
d2l.corr2d)。- 结果融合:将所有通道的运算结果逐元素相加,得到最终单通道输出。
输入要求:
X的形状为(输入通道数, 高度, 宽度)(如(2, 3, 3))。K的形状为(输入通道数, 卷积核高度, 卷积核宽度)(如(2, 2, 2))。- 输入通道数必须相同,否则无法配对。
二、执行流程详解
1.
zip(X, K)将输入张量
X和卷积核K按通道维度(第 0 维)拆解并配对:
X[0]与K[0]配对(第 1 个输入通道与第 1 个卷积核)。X[1]与K[1]配对(第 2 个输入通道与第 2 个卷积核)。- 以此类推,直到所有通道完成配对。
示例(假设
X和K各有 2 个通道):# 输入X:2通道,每个通道3×3 X = [ [[0,1,2], [3,4,5], [6,7,8]], # 通道0 [[1,2,3], [4,5,6], [7,8,9]] # 通道1 ] # 卷积核K:2个2×2卷积核 K = [ [[0,1], [2,3]], # 卷积核0(对应通道0) [[1,2], [3,4]] # 卷积核1(对应通道1) ] # zip(X, K) 生成两个元组: # 1. (X[0], K[0]) → (通道0输入, 卷积核0) # 2. (X[1], K[1]) → (通道1输入, 卷积核1)2.
d2l.corr2d(x, k)对每对通道执行单通道互相关运算:
x:单个通道的输入矩阵(如3×3)。k:对应的卷积核(如2×2)。- 输出:单个通道的互相关结果(如
2×2,尺寸由x和k的大小决定)。示例计算(以第一对通道为例):
# 输入通道0: x0 = [[0,1,2], [3,4,5], [6,7,8]] # 卷积核0: k0 = [[0,1], [2,3]] # 单通道互相关计算: # 位置(0,0):(0×0 + 1×1) + (3×2 + 4×3) = 19 # 位置(0,1):(1×0 + 2×1) + (4×2 + 5×3) = 25 # 位置(1,0):(3×0 + 4×1) + (6×2 + 7×3) = 37 # 位置(1,1):(4×0 + 5×1) + (7×2 + 8×3) = 43 # 输出:[[19,25], [37,43]]3.
sum(...)将所有通道的互相关结果逐元素相加:
- 假设
X有C个通道,则sum会将C个单通道结果相加。- 要求所有单通道结果尺寸相同(否则无法相加)。
示例(假设两个通道的结果分别为
A和B):# 通道0结果: A = [[19,25], [37,43]] # 通道1结果: B = [[37,47], [67,77]] # 最终输出: sum = [[19+37, 25+47], [37+67, 43+77]] = [[56,72], [104,120]]三、数学原理与公式
1. 单通道互相关公式
2. 多通道互相关公式
详解torch.stack([corr2d_multi_in(X, k) for k in K], 0)?
一、功能概述
这行代码的核心功能是:
- 对卷积核张量
K中的每个子卷积核(对应一个输出通道),与输入X执行多输入单输出通道的互相关运算(通过corr2d_multi_in实现)。- 将所有单输出通道的结果在第 0 维度(输出通道维度) 堆叠,形成多输出通道的张量。
输入输出形状:
- 输入
X:形状为(输入通道数, 高度, 宽度)(如(2, 3, 3))。- 输入
K:形状为(输出通道数, 输入通道数, 卷积核高度, 卷积核宽度)(如(3, 2, 2, 2))。- 输出:形状为
(输出通道数, 输出高度, 输出宽度)(如(3, 2, 2))。二、执行流程拆解
1. 列表推导式:
[corr2d_multi_in(X, k) for k in K]
- 遍历卷积核
K的第 0 维度:K中的每个元素k是一组对应单个输出通道的卷积核(形状为(输入通道数, 卷积核高度, 卷积核宽度))。- 调用
corr2d_multi_in(X, k):对输入X和当前输出通道的卷积核k执行多输入单输出运算,得到一个单通道特征图(形状为(输出高度, 输出宽度))。示例(假设
K有 3 个输出通道):# K的形状:(3, 2, 2, 2) → 3个输出通道,每个通道含2个2×2卷积核 K = [ k0, # 第0个输出通道的卷积核(形状:(2, 2, 2)) k1, # 第1个输出通道的卷积核(形状:(2, 2, 2)) k2 # 第2个输出通道的卷积核(形状:(2, 2, 2)) ] # 列表推导式的结果是3个单通道特征图: [ corr2d_multi_in(X, k0), # 第0输出通道(形状:(2, 2)) corr2d_multi_in(X, k1), # 第1输出通道(形状:(2, 2)) corr2d_multi_in(X, k2) # 第2输出通道(形状:(2, 2)) ]2.
torch.stack(..., 0):在第 0 维度堆叠
torch.stack功能:将多个形状相同的张量在指定维度拼接,新增该维度作为堆叠后的第 0 维。- 维度选择
0:指定堆叠后的第 0 维度为输出通道维度,因此最终输出的形状为(输出通道数, 输出高度, 输出宽度)。示例(承接上文列表推导式的结果):
# 3个单通道特征图(形状均为(2,2)) tensor0 = [[56, 72], [104, 120]] # 第0输出通道 tensor1 = [[100, 128], [188, 224]] # 第1输出通道 tensor2 = [[144, 184], [272, 328]] # 第2输出通道 # 在第0维度堆叠后: result = torch.stack([tensor0, tensor1, tensor2], 0) # 形状:(3, 2, 2),即(输出通道数, 高度, 宽度)三、数学意义与多输出通道的作用
1. 多输出通道的本质
每个输出通道对应一组独立的卷积核,用于提取输入
X中不同类型的特征:
- 第 1 个输出通道:可能提取边缘特征。
- 第 2 个输出通道:可能提取纹理特征。
- 第 3 个输出通道:可能提取颜色特征。
通过多输出通道,神经网络可以同时捕捉输入数据的多种特征,提升表达能力。
2. 数学表达式
torch.stack 与 torch.cat 的区别?
torch.stack:新增维度并堆叠,要求所有输入张量形状完全相同(如 3 个(2,2)张量堆叠为(3,2,2))。torch.cat:在已有维度上拼接,不新增维度(如 3 个(2,2)张量在第 0 维拼接为(6,2))。此处必须用torch.stack,因为需要新增 “输出通道维度”。
完整代码
"""
文件名: 6.4 卷积神经网络中的多输入多输出通道
作者: 墨尘
日期: 2025/7/13
项目名: dl_env
备注: 实现多输入通道和多输出通道的二维互相关运算
"""
import torch
from d2l import torch as d2l # 导入d2l库中的torch工具(包含基础互相关函数)
def corr2d_multi_in(X, K):
"""
多输入单输出通道的二维互相关运算
参数:
X: 输入张量,形状为(输入通道数, 高度, 宽度) (2,3,3)
K: 卷积核张量,形状为(输入通道数, 卷积核高度, 卷积核宽度) (2,2,2)
返回:
单通道输出张量,形状为(输出高度, 输出宽度)
"""
# 1. 遍历输入通道和对应卷积核(zip实现一一配对)
# 2. 对每个通道执行单通道互相关运算(d2l.corr2d)
# 3. 将所有通道结果求和,得到单通道输出
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
def corr2d_multi_in_out(X, K):
"""
多输入多输出通道的二维互相关运算
参数:
X: 输入张量,形状为(输入通道数, 高度, 宽度)
K: 卷积核张量,形状为(输出通道数, 输入通道数, 卷积核高度, 卷积核宽度)
返回:
多通道输出张量,形状为(输出通道数, 输出高度, 输出宽度)
"""
# 1. 遍历输出通道维度(K的第0维,每个元素是一组卷积核)
# 2. 每组卷积核与输入X执行多输入单输出互相关(调用corr2d_multi_in)
# 3. 用torch.stack将所有输出通道堆叠成多通道张量
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
if __name__ == '__main__':
# ------------------------------
# 步骤1: 定义多输入通道数据和卷积核
# ------------------------------
# 2个输入通道,每个通道为3×3矩阵(形状:(2, 3, 3))
X = torch.tensor([
[[0.0, 1.0, 2.0], # 第1个通道
[3.0, 4.0, 5.0],
[6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], # 第2个通道
[4.0, 5.0, 6.0],
[7.0, 8.0, 9.0]]
])
# 2个输入通道对应的卷积核(形状:(2, 2, 2))
# 第1个卷积核对应第1个输入通道,第2个卷积核对应第2个输入通道
K = torch.tensor([
[[0.0, 1.0], # 第1个卷积核(对应第1输入通道)
[2.0, 3.0]],
[[1.0, 2.0], # 第2个卷积核(对应第2输入通道)
[3.0, 4.0]]
])
# ------------------------------
# 步骤2: 测试多输入单输出通道运算
# ------------------------------
print("===== 多输入单输出通道结果 =====")
multi_in_single_out = corr2d_multi_in(X, K)
print(multi_in_single_out)
# 输出解释:2×2矩阵,由两个通道的互相关结果求和得到
# tensor([[ 56., 72.],
# [104., 120.]])
# ------------------------------
# 步骤3: 构建多输出通道卷积核
# ------------------------------
# 用torch.stack在第0维堆叠3组卷积核(原始K、K+1、K+2)
# 新形状:(3, 2, 2, 2) → 3个输出通道,每个通道2个2×2卷积核
K_multi_out = torch.stack((K, K + 1, K + 2), 0)
print("\n===== 多输出通道卷积核形状 =====")
print(K_multi_out.shape) # 输出:torch.Size([3, 2, 2, 2])
# ------------------------------
# 步骤4: 测试多输入多输出通道运算
# ------------------------------
print("\n===== 多输入多输出通道结果 =====")
multi_in_multi_out = corr2d_multi_in_out(X, K_multi_out)
print(multi_in_multi_out)
# 输出解释:3个输出通道,每个通道为2×2矩阵
# tensor([[[ 56., 72.],
# [104., 120.]],
#
# [[100., 128.],
# [188., 224.]],
#
# [[144., 184.],
# [272., 328.]]])实验结果

更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容


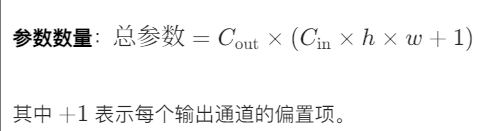









所有评论(0)