神经网络常见激活函数求导
sigmoid(x)=1+e−x1sigmoid′(x)=(1+e−x1)′=(1+e−x)20−(1+e−x)′=(1+e−x)2e−x=(1+e−x)(1+e−x)1+e−x−1=(1+e−x)1+e−x−1.(1+e−x)1=[1。
神经网络常见激活函数求导推导
1. 求导
1.1 求导公式

1.2 求导含义
- 导数:表示某个瞬间的变化量
- x的 “微小变化” 将导致函数
f(x)的值在多大程度上发生变化 - 微小变化的
h无限趋近0
d f ( x ) d x = lim h → 0 f ( x + h ) − f ( x ) h \begin{aligned} \frac{df(x)}{dx}&=\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \end{aligned} dxdf(x)=h→0limhf(x+h)−f(x)
- x的 “微小变化” 将导致函数
2. 常见激活函数
2.1 sigmoid函数
-
原函数
s i g m o i d ( x ) = 1 1 + e − x \begin{aligned} sigmoid(x) &= \frac{1}{1 +e^{-x}} \end{aligned} sigmoid(x)=1+e−x1 -
函数图
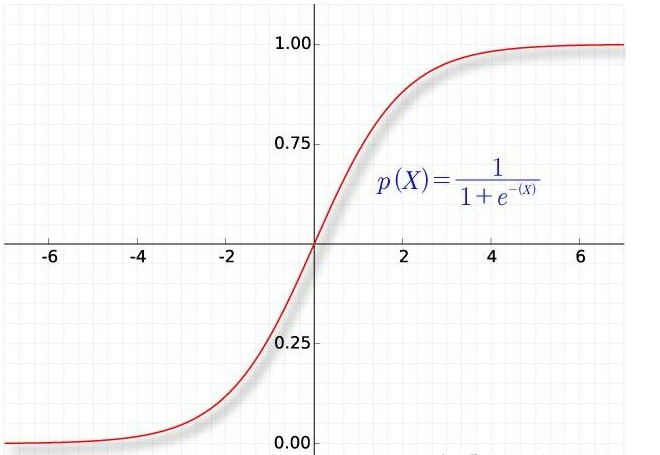
-
求导过程
s i g m o i d ′ ( x ) = ( 1 1 + e − x ) ′ = 0 − ( 1 + e − x ) ′ ( 1 + e − x ) 2 = e − x ( 1 + e − x ) 2 = 1 + e − x − 1 ( 1 + e − x ) ( 1 + e − x ) = 1 + e − x − 1 ( 1 + e − x ) . 1 ( 1 + e − x ) = [ 1 − 1 ( 1 + e − x ) ] . 1 ( 1 + e − x ) = [ 1 − s i g m o i d ( x ) ] ∗ s i g m o i d ( x ) \begin{aligned} sigmoid'(x) &= (\frac{1}{1 +e^{-x}})' \\&=\frac{0-(1 +e^{-x})'}{(1 +e^{-x})^2} \\&=\frac{e^{-x}}{(1 +e^{-x})^2} \\&=\frac{1+e^{-x}-1}{(1 +e^{-x})(1 +e^{-x})} \\&=\frac{1+e^{-x}-1}{(1 +e^{-x})}.\frac{1}{(1 +e^{-x})} \\&=[1-\frac{1}{(1 +e^{-x})}].\frac{1}{(1 +e^{-x})} \\&=[1-sigmoid(x)]*sigmoid(x) \end{aligned} sigmoid′(x)=(1+e−x1)′=(1+e−x)20−(1+e−x)′=(1+e−x)2e−x=(1+e−x)(1+e−x)1+e−x−1=(1+e−x)1+e−x−1.(1+e−x)1=[1−(1+e−x)1].(1+e−x)1=[1−sigmoid(x)]∗sigmoid(x)
2.2 Tanh函数
-
原函数
T a n h ( x ) = e x − e − x e x + e − x \begin{aligned} Tanh(x) &=\frac{e^x-e^{-x}}{e^x+e^{-x}} \end{aligned} Tanh(x)=ex+e−xex−e−x -
函数图
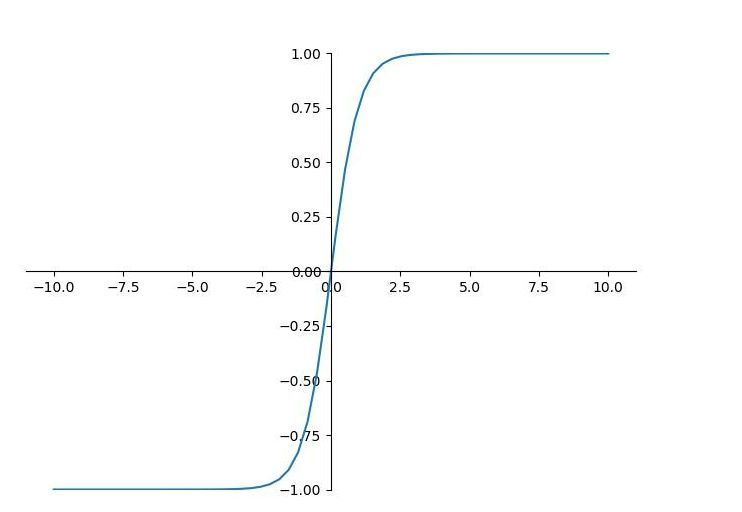
-
求导过程
T a n h ′ ( x ) = e x − e − x e x + e − x ) ′ = ( e x − e − x ) ′ ( e x + e − x ) − ( e x − e − x ) ( e x + e − x ) ′ ( e x + e − x ) 2 = ( e x + e − x ) ( e x + e − x ) − ( e x − e − x ) ( e x − e − x ) ( e x + e − x ) 2 = ( e x + e − x ) 2 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − ( e x − e − x e x + e − x ) 2 = 1 − T a n h 2 ( x ) \begin{aligned} Tanh'(x) &=\frac{e^x-e^{-x}}{e^x+e^{-x}})' \\&=\frac{(e^x-e^{-x})'(e^x+e^{-x})-(e^x-e^{-x})(e^x+e^{-x})'}{(e^x+e^{-x})^2} \\&=\frac{(e^x+e^{-x})(e^x+e^{-x})-(e^x-e^{-x})(e^x-e^{-x})}{(e^x+e^{-x})^2} \\&=\frac{(e^x+e^{-x})^2-(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \\&=1-\frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \\&=1-(\frac{e^x-e^{-x}}{e^x+e^{-x}})^2 \\&=1-Tanh^2(x) \end{aligned} Tanh′(x)=ex+e−xex−e−x)′=(ex+e−x)2(ex−e−x)′(ex+e−x)−(ex−e−x)(ex+e−x)′=(ex+e−x)2(ex+e−x)(ex+e−x)−(ex−e−x)(ex−e−x)=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−(ex+e−x)2(ex−e−x)2=1−(ex+e−xex−e−x)2=1−Tanh2(x)
2.3 ReLU函数
-
原函数
R e l u ( x ) = { x x ≥ 0 0 x < 0 Relu(x)=\begin{cases} x & x\geq0 \\ 0 & x <0 \end{cases} Relu(x)={x0x≥0x<0 -
函数图
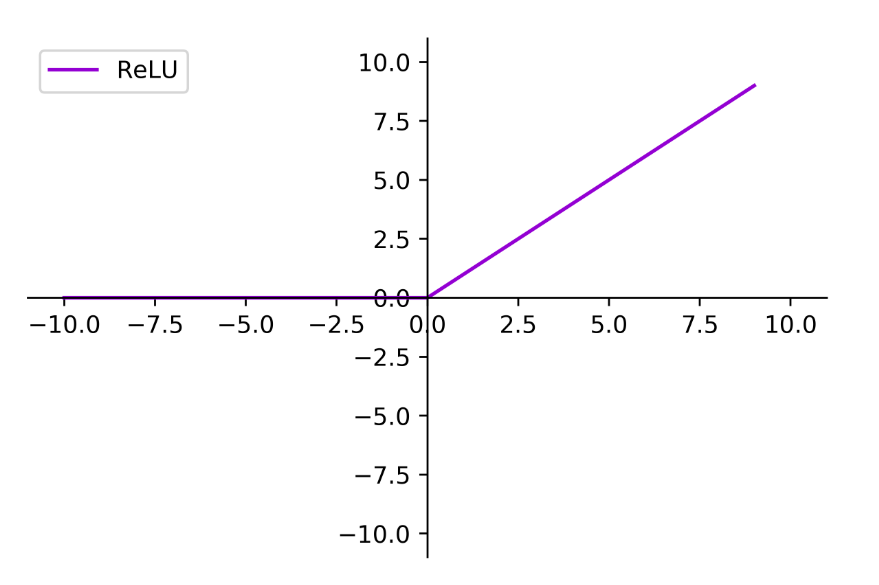
-
求导
R e l u ′ ( x ) = { 1 x ≥ 0 0 x < 0 Relu'(x) =\begin{cases} 1 & x\geq0 \\ 0 & x <0 \end{cases} Relu′(x)={10x≥0x<0
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容







所有评论(0)