卷积神经网络在轴承故障诊断【附代码】
滚动轴承在众多工业领域中起着至关重要的作用,然而长时间处于高负荷工作环境下的滚动轴承,一旦发生故障,可能会引发严重的人员伤亡和巨大的经济损失。传统的轴承故障诊断方法依赖人工,效率低下。现有的基于卷积神经网络的轴承诊断方法虽在一定程度上提高了工作效率,但仍存在提取关键故障特征能力不足的问题,导致模型诊断的准确率不高。✅博主简介:本人擅长建模仿真、数据分析、论文写作与指导,项目与课题经验交流。项目合作
·

✅博主简介:本人擅长建模仿真、数据分析、论文写作与指导,项目与课题经验交流。项目合作可私信或扫描文章底部二维码。
滚动轴承在众多工业领域中起着至关重要的作用,然而长时间处于高负荷工作环境下的滚动轴承,一旦发生故障,可能会引发严重的人员伤亡和巨大的经济损失。传统的轴承故障诊断方法依赖人工,效率低下。现有的基于卷积神经网络的轴承诊断方法虽在一定程度上提高了工作效率,但仍存在提取关键故障特征能力不足的问题,导致模型诊断的准确率不高。
一、改进的多尺度卷积神经网络(IMCNN)故障诊断方法
- 解决的问题
- 滚动轴承在故障诊断过程中容易受到外界噪声干扰,同时深层网络中由于特征尺度不同,容易导致提取特征信息不充分。为了解决这些问题,提出了改进的多尺度卷积神经网络(IMCNN)的故障诊断方法。
- 加噪仿真实验
- 进行加噪仿真实验,以验证该方法在噪声干扰情况下的性能。实验结果表明,IMCNN 方法在噪声干扰的情况下诊断精度可以达到 91% 左右,显示出了较强的抗噪能力和较高的诊断准确性。
二、基于贝叶斯改进的 IMCNN 算法(BO-IIMCNN)故障诊断算法
- 针对的问题
- 在滚动轴承故障诊断过程中,时序特征难以提取。为了解决这个问题,提出了具有创新性的基于贝叶斯改进的 IMCNN 算法,即 BO-IIMCNN(Bayesian Optimization for Improved IMCNN)故障诊断算法。
- 算法的改进
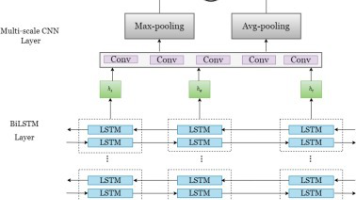
- BO-IIMCNN 算法在 IMCNN 的基础上引入了双向门控循环神经网络。双向门控循环神经网络能够更好地捕捉轴承故障数据中的时序特征,提高模型对故障的诊断能力。
- 加入了一种具有强特征提取能力的注意力增强机制。这种注意力增强机制可以使模型更加关注关键的故障特征,进一步提高特征提取的能力和诊断的准确性。
三、仿真实验验证及优势
- 特征提取能力强
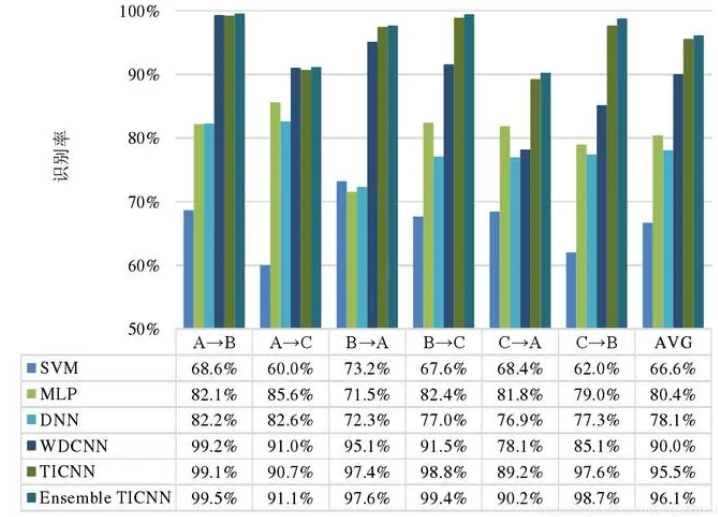
- 通过仿真实验验证,BOIIMCNN 算法具有很强的特征提取能力。与传统的卷积神经网络算法相比,BOIIMCNN 算法能够更好地提取轴承故障数据中的关键特征,从而提高诊断的准确性。
- 诊断精度高
- BOIIMCNN 算法的诊断精度高于传统的卷积神经网络算法。在不同的实验条件下,BOIIMCNN 算法都能够保持较高的诊断精度,显示出了较强的稳定性和可靠性。
- 稳定性强
- BOIIMCNN 算法具有较强的稳定性。在高噪声环境下,BOIIMCNN 算法仍然能够保持较高的诊断精度,说明该算法对噪声具有较好的鲁棒性。
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout, Bidirectional, GRU
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import Adam
from sklearn.model_selection import train_test_split
# 加载轴承数据
bearing_data = np.load('bearing_data.npy')
labels = np.load('bearing_labels.npy')
# 数据预处理
X_train, X_test, y_train, y_test = train_test_split(bearing_data, labels, test_size=0.2, random_state=42)
# 定义改进的多尺度卷积神经网络(IMCNN)模型
def imcnn_model():
model = Sequential()
model.add(Conv1D(32, 3, activation='relu', input_shape=(X_train.shape[1], 1)))
model.add(MaxPooling1D(2))
model.add(Conv1D(64, 3, activation='relu'))
model.add(MaxPooling1D(2))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(len(np.unique(y_train)), activation='softmax'))
return model
# 定义基于贝叶斯改进的 IMCNN 算法(BO-IIMCNN)模型
def bo_iimcnn_model():
model = Sequential()
model.add(Conv1D(32, 3, activation='relu', input_shape=(X_train.shape[1], 1)))
model.add(MaxPooling1D(2))
model.add(Conv1D(64, 3, activation='relu'))
model.add(MaxPooling1D(2))
model.add(Bidirectional(GRU(64)))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(len(np.unique(y_train)), activation='softmax'))
return model
# 训练 IMCNN 模型
imcnn_model = imcnn_model()
imcnn_model.compile(optimizer=Adam(learning_rate=0.001), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
imcnn_history = imcnn_model.fit(X_train.reshape(-1, X_train.shape[1], 1), y_train, epochs=50, batch_size=32, validation_split=0.2)
# 训练 BO-IIMCNN 模型
bo_iimcnn_model = bo_iimcnn_model()
bo_iimcnn_model.compile(optimizer=Adam(learning_rate=0.001), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
bo_iimcnn_history = bo_iimcnn_model.fit(X_train.reshape(-1, X_train.shape[1], 1), y_train, epochs=50, batch_size=32, validation_split=0.2)
# 评估模型
imcnn_loss, imcnn_acc = imcnn_model.evaluate(X_test.reshape(-1, X_test.shape[1], 1), y_test)
bo_iimcnn_loss, bo_iimcnn_acc = bo_iimcnn_model.evaluate(X_test.reshape(-1, X_test.shape[1], 1), y_test)
print(f'IMCNN 模型准确率:{imcnn_acc}')
print(f'BO-IIMCNN 模型准确率:{bo_iimcnn_acc}')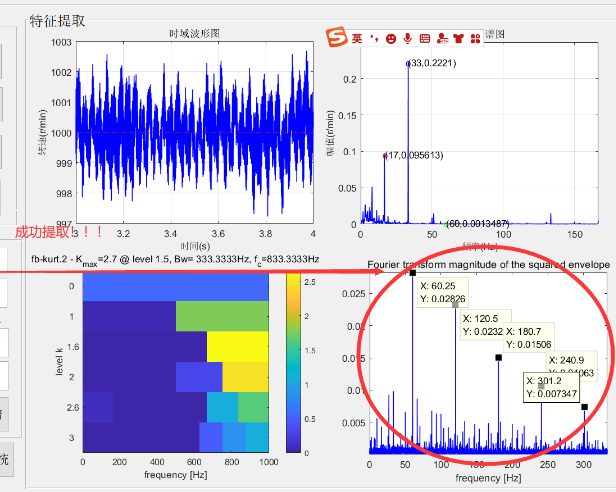
更多推荐
 已为社区贡献82条内容
已为社区贡献82条内容








所有评论(0)