跟着问题学13——RNN循环神经网络结构详解及代码实战

再来看一下序列T_seq和通道channel，RNN系列的序列T_seq是指一个连续的输入，比如一句话，一周的股票信息，而且这个序列是有时间先后顺序且互相关联的，而CNN系列的通道channel则是指不同角度的特征，比如彩色图像的RGB三色通道，过程中每个通道代表提取了每个方面的特征，不同通道之间是没有强相关性的，不过也可以进行融合。输入不是序列而输出为序列的情况怎么处理？但卷积神经网络并不能处理

weixin_42251091

1949人浏览 · 2024-12-08 17:30:00

weixin_42251091 · 2024-12-08 17:30:00 发布

1 循环神经网络的基本网络结构

循环神经网络简介

在前面学习的传统神经网络或卷积神经网络，其输入是向量或多维张量且是一次性输入到网络中的，并不考虑先后顺序。但在很多实际问题中，存在着很多序列型的数据（文本、语音，股票以及视频等）。什么是序列信息呢？通俗理解就是一段连续的信息，前后信息之间是有关系的，必须将不同时刻的信息放在一起理解。而且网络的输出也是和多个时刻的输入（甚至整个输入）都是有关系的。

但卷积神经网络并不能处理好这种关联性，不同时刻的输入之间是没有关联的，没有记忆能力，所以前面时刻的输出不能传递到后面的时刻。

因此，就有了循环神经网络（Recurrent Neural Network，RNN），其本质是：当前的输出同时依赖于当前的输入和之前的输入（可以以不同的形式记忆下来），也就意味着拥有记忆的能力。

比如：我喜欢吃X，吃是一个动词，按照语法规则，它后面接名词的概率就比较大，在预测X是什么的时候就要考虑前面的动词吃的信息，如果没考虑上下文信息而预测X是一个动词的话，动词+动词，很大概率是不符合语言逻辑的。

RNN相比卷积神经网络，为了适应能够记忆前面时序的内容，其结构有诸多变化，往往让初学者感到困惑，下面我们首先详细对比介绍一下RNN的网络结构。

前面我们讲到，神经网络的各种结构都是为了挖掘变换数据特征的，所以下面我们也将结合数据特征的维度来对比介绍一下RNN的网络结构。

传统神经网络结构

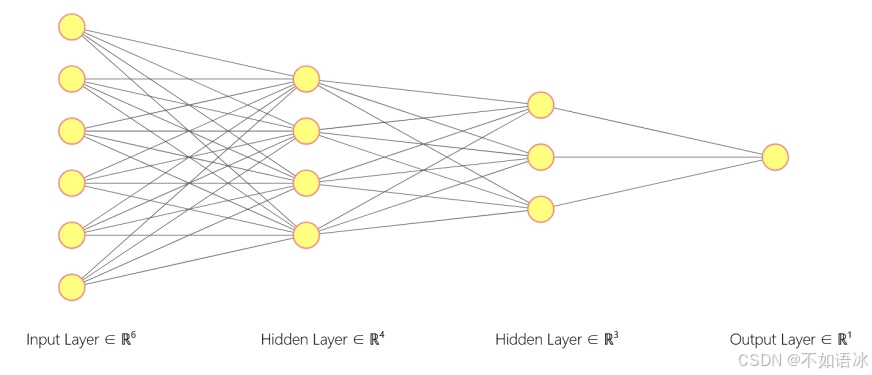
从特征角度考虑：

输入特征：是n*1的单维向量（这也是为什么卷积神经网络在linear层前要把所有特征层展平），

隐藏层：然后根据隐藏层神经元的数量m将前层输入的特征用m*1的单维向量进行表示（对特征进行了提取变换，隐藏层的数据特征），单个隐藏层的神经元数量就代表网络参数，可以设置多个隐藏层；

输出特征：最终根据输出层的神经元数量y输出y*1的单维向量。

卷积神经网络结构

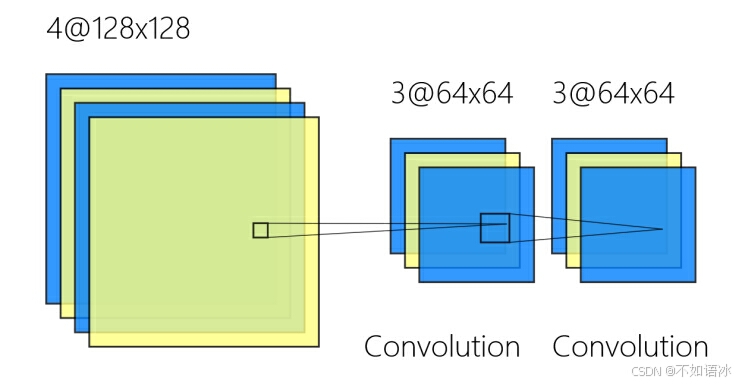
从特征角度考虑：

输入特征：是(batch)*channel*width*height的张量，

卷积层（等）：然后根据输入通道channel的数量c_in和输出通道channel的数量c_out会有c_out*c_in*k*k个卷积核将前层输入的特征进行卷积（对特征进行了提取变换，k为卷积核尺寸），卷积核的大小和数量c_out*c_in*k*k就代表网络参数，可以设置多个卷积层；每一个channel都代表提取某方面的一种特征，该特征用width*height的二维张量表示，不同特征层之间是相互独立的（可以进行融合）。

输出特征：根据场景的需要设置后面的输出，可以是多分类的单维向量等等。

循环神经网络RNN结构

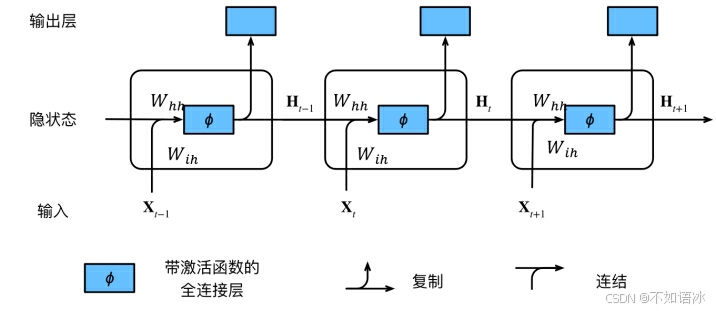
从特征角度考虑：

输入特征：是(batch)*T_seq*feature_size的张量（T_seq代表序列长度，注意不是batch_size）.

我们来详细对比一下卷积神经网络的输入特征，

(batch)*T_seq*feature_size

(batch)*channel*width*height，

逐个进行分析，RNN系列的基础输入特征表示是feature_size*1的单维向量，比如一个单词的词向量，比如一个股票价格的影响因素向量，而CNN系列的基础输入特征是width*height的二维张量；

最后就是batch，两者都有，在RNN系列，batch就是有多个句子，在CNN系列，就是有多张图片（每个图片可以有多个通道）

隐藏层：明确了输入特征之后，我们再来看看隐藏层代表着什么。隐藏层有T_seq个隐状态H_t（和输入序列长度相同），每个隐状态H_t类似于一个channel，对应着T_seq中的t时刻的输入特征；而每个隐状态H_t是用hidden_size*1的单维向量表示的，所以一个隐含层是T_seq*hidden_size的张量；对应时刻t的输入特征由feature_size*1变为hidden_size*1的向量。如图中所示，同一个隐含层不同时刻的参数W_ih和W_hh是共享的；隐藏层可以有num_layers个（图中只有1个）

以t时刻具体阐述一下：

X_t是t时刻的输入，是一个feature_size*1的向量

W_ih是输入层到隐藏层的权重矩阵

H_t是t时刻的隐藏层的值,是一个hidden_size*1的向量

W_hh是上一时刻的隐藏层的值传入到下一时刻的隐藏层时的权重矩阵

Ot是t时刻RNN网络的输出

从上右图中可以看出这个RNN网络在t时刻接受了输入Xt之后，隐藏层的值是St，输出的值是Ot。但是从结构图中我们可以发现St并不单单只是由Xt决定，还与t-1时刻的隐藏层的值St-1有关。

怎么理解这个参数共享呢？

虽然说X{t-1}，X{t}，X{t+1}是表示不同时刻的输入，但是他们输入到RNN网络中的时候并不是作为单独的向量一个一个输入地，而是组合在一起形成一个矩阵输入，然后这个矩阵再通过权重矩阵U的变化，其实是同一时刻输入地，只是计算的先后顺序不同。因此同一个隐藏层中，不同时刻的输入他们的W，V，U参数是共享地。

输出特征：最终的输出可以根据需要，保留所有隐状态或只保留最后时刻的隐状态。

RNN网络结构的数学公式

前面从概念上介绍了RNN网络结构和输入输出隐藏层，接下来具体探索一下其用数学公式的表达。

首先给定一个序列输入句子，假设这个句子有4个词语，定义为x1、x2、x3、x4，

然后我们依次看一下隐状态是如何计算的，先从h1的计算开始看：

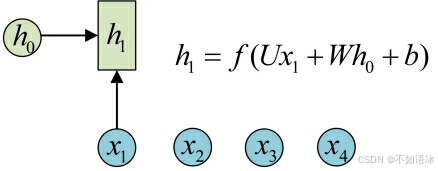
这里的h0是假设给定的先验值，也是需要训练优化的。

图示中记号的含义是：

圆圈或方块表示的是向量。
一个箭头就表示对该向量做一次变换。如上图中h0和x1分别有一个箭头连接，就表示对h0和x1各做了一次变换。

h2的计算和h1类似。要注意的是，在计算时，每一步使用的参数U、W、b都是一样的，也就是说每个步骤的参数都是共享的，这是RNN的重要特点，一定要牢记。

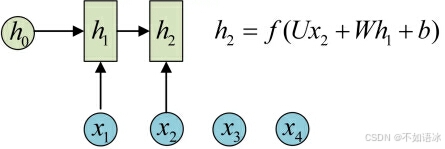
依次计算剩下来的（使用相同的参数U、W、b）：

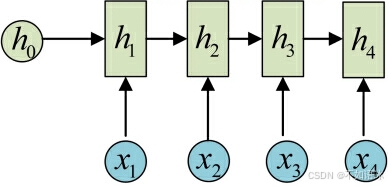
这里为了方便起见，只画出序列长度为4的情况，实际上，这个计算过程可以无限地持续下去。

然后这只是计算了一个隐藏层，事实上可以像CNN那样，继续把隐藏层的状态作为新的输入特征，继续传递到下一个隐藏层挖掘转换特征。

目前的RNN还没有输出，得到输出值的方法就是直接通过h进行计算：

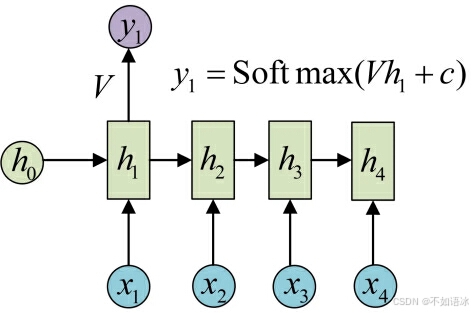
正如之前所说，一个箭头就表示对对应的向量做一次类似于f(Wx+b)的变换，这里的这个箭头就表示对h1进行一次变换，得到输出y1。

剩下的输出类似进行（使用和y1同样的参数V和c）：

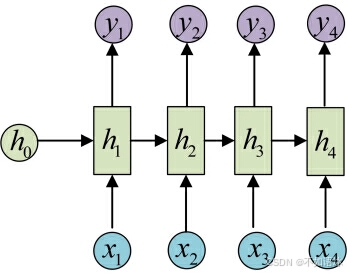
这就是最经典的RNN结构，它的输入是x1, x2, .....xn，输出为y1, y2, ...yn，也就是说，输入和输出序列必须要是等长的。

由于这个限制的存在，经典RNN的适用范围比较小，但也有一些问题适合用经典的RNN结构建模，如：

计算视频中每一帧的分类标签。因为要对每一帧进行计算，因此输入和输出序列等长。
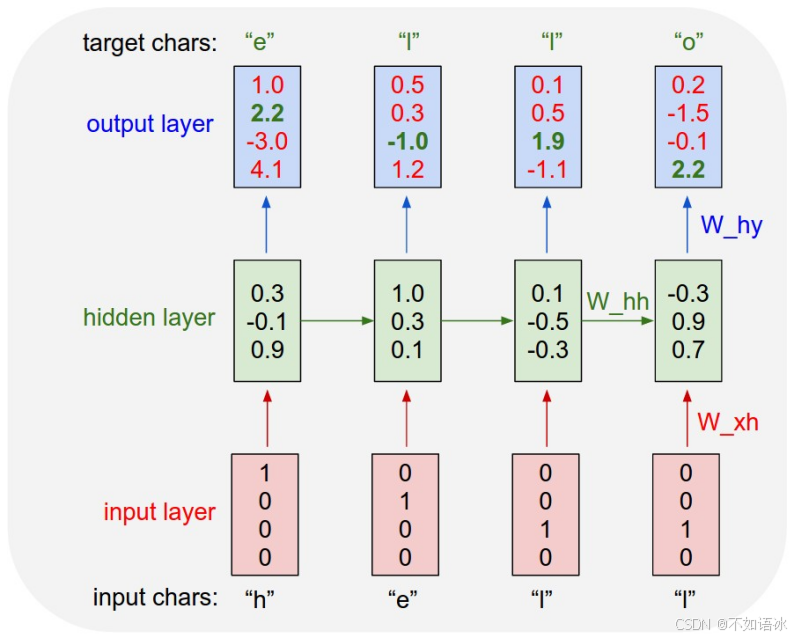
输入为字符，输出为下一个字符的概率。这就是著名的Char RNN

（详细介绍请参考：The Unreasonable Effectiveness of Recurrent Neural Networks，Char RNN可以用来生成文章，诗歌，甚至是代码，非常有意思）。

2 RNN结构分类

前面在介绍RNN经典网络结构的时候，我们对比分析了输入输出的基本特征是什么样的，而且输入输出是等长的。在实际应用中，根据输入输出长度的不同，RNN又分为几种不同的形式，概括起来如下图所示：

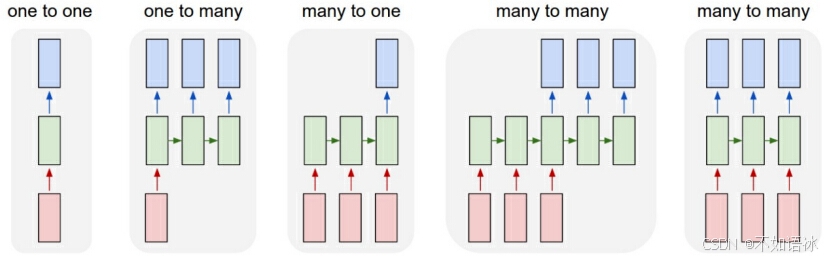
N VS 1

有的时候，我们要处理的问题输入是一个序列，输出是一个单独的值而不是序列，应该怎样建模呢？实际上，我们只在最后一个h上进行输出变换就可以了：

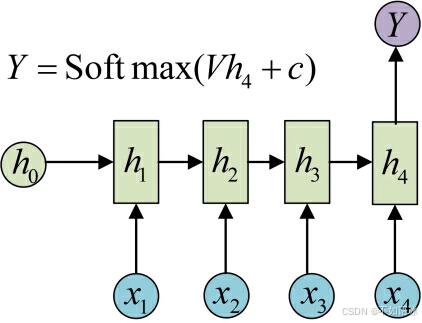
这种结构通常用来处理序列分类问题。如输入一段文字判别它所属的类别，输入一个句子判断其情感倾向，输入一段视频并判断它的类别等等。

1 VS N

输入不是序列而输出为序列的情况怎么处理？我们可以只在序列开始进行输入计算，如左图，还有一种结构是把输入信息X作为每个阶段的输入，如右图：

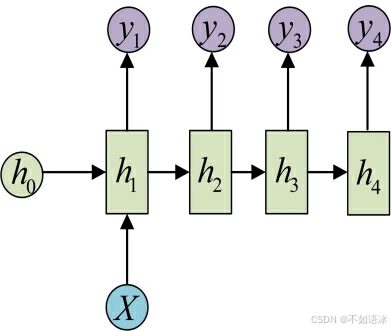
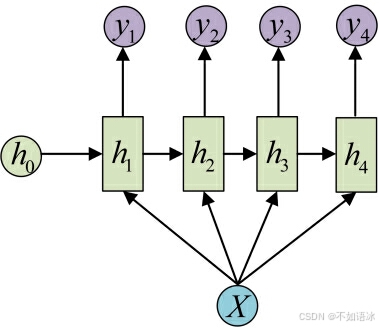
这种1 VS N的结构可以处理的问题有：

从图像生成文字（image caption），此时输入的X就是图像的特征，而输出的y序列就是一段句子
从类别生成语音或音乐等

N vs M

下面先简单介绍RNN最重要的一个变种：N vs M。这种结构又叫Encoder-Decoder模型，也可以称之为Seq2Seq模型。

经典的N vs N RNN要求序列等长，然而我们遇到的大部分问题序列都是不等长的，如机器翻译中，源语言和目标语言的句子往往并没有相同的长度。

为此，Encoder-Decoder结构先将输入数据编码成一个上下文中间向量c：

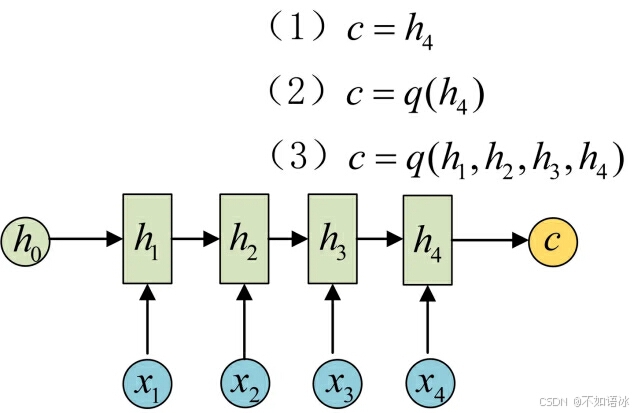
得到c有多种方式，最简单的方法就是把Encoder的最后一个隐状态赋值给c，还可以对最后的隐状态做一个变换得到c，也可以对所有的隐状态做变换。

拿到c之后，就用另一个RNN网络对其进行解码，这部分RNN网络被称为Decoder。具体做法就是将c当做之前的初始状态h0输入到Decoder中：

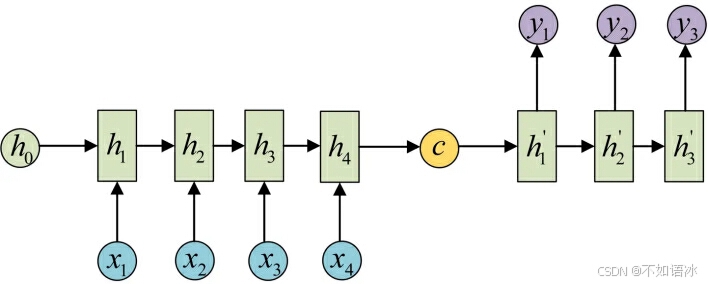
还有一种做法是将c当做每一步的输入：

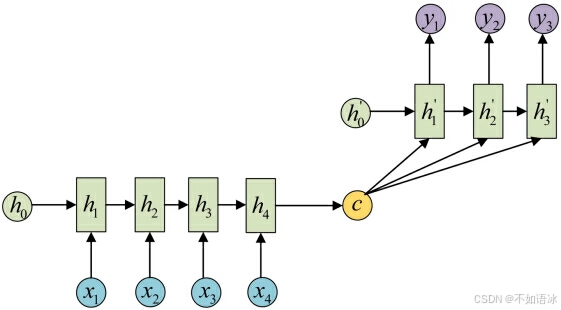
由于这种Encoder-Decoder结构不限制输入和输出的序列长度，因此应用的范围非常广泛，比如：

机器翻译。Encoder-Decoder的最经典应用，事实上这一结构就是在机器翻译领域最先提出的
文本摘要。输入是一段文本序列，输出是这段文本序列的摘要序列。
阅读理解。将输入的文章和问题分别编码，再对其进行解码得到问题的答案。
语音识别。输入是语音信号序列，输出是文字序列。
…………

3代码

模型里使用两种方法创建，一种是直接调用pytorch框架里的模型，熟悉参数及调用流程，另一种是手写了rnn函数的具体计算过程，学习内部结构是什么样的。

model.py

import torch
import torch.nn as nn

import random
#直接使用pytorch自带的RNN类
#可以看到，RNN网络也是继承自nn.Module的
class RNN(nn.Module):
    #这里的输入参数包括最开始输入特征“词向量”维度，隐藏层的每个隐状态的特征维度，隐藏层数量，输出层的特征维度（一般和隐状态特征维度一致）
    def __init__(self,feature_size,hidden_size,num_layers,output_size):
        super(RNN,self).__init__()

        self.rnn=nn.RNN(
            input_size=feature_size,hidden_size=hidden_size,
            num_layers=num_layers,batch_first=True
        )
        #参数初始化，
        for k in self.rnn.parameters():
            nn.init.normal_(k,mean=0.0,std=0.001)
        #linear层的输入和输出的维度可以是任意的,只需要保证最后一个维度是特征维度in_features&out_features就行
        # #- Input: :math:`(*, H_{in})` where :math:`*` means any number of
        #   dimensions including none and :math:`H_{in} = \text{in\_features}`.
        # - Output: :math:`(*, H_{out})` where all but the last dimension
        #   are the same shape as the input and :math:`H_{out} = \text{out\_features}`.
        #
        # Examples::
        # >> > m = nn.Linear(20, 30)
        # >> > input = torch.randn(128, 20)
        # >> > output = m(input)
        # >> > print(output.size())
        # torch.Size([128, 30])
        self.linear=nn.Linear(hidden_size,output_size)
        self.hidden_size=hidden_size

    def forward(self,x,hidden_prev):
        #每一次调用rnn层返回的就是输出层和隐状态值，隐状态又是下一循环的上一状态值，所以用hidden_prev表示
        out,hidden_prev=self.rnn(x,hidden_prev)
        print("out1&hidden_prev.shape",out.shape,hidden_prev.shape)
        #view()相当于reshape、resize，重新调整PyTorch 中的 Tensor 形状，若非 Tensor 类型，可使用 data = torch.tensor(data)来进行转换。
       # out=out.view(-1,self.hidden_size)
        print("out2.shape", out.shape)
        out=self.linear(out)
        print("out3.shape", out.shape)
       # out=out.unsqueeze(0)
        print("out4.shape", out.shape)
        #输出的维度是batch_size*T_seq*hidden_size
        return out,hidden_prev

#自己实现一个RNN函数
#这里的函数参数需要手动给定网络结构参数，
def rnn_forward(input,weight_ih,weight_hh,bias_ih,bias_hh,h_prev):
    #input的shape就是batch_size*T_seq*feature_size(设置batch_first=TRUE)
    batch_size,T_seq,feature_size=input.shape
    hidden_size=weight_ih.shape[0]
    h_out=torch.zeros(batch_size,T_seq,hidden_size)
    for t in range(T_seq):
        x=input[:,t,:].unsqueeze(2)
      #  print("xt.shape",x.shape)
            #unsqueeze，在给定维度上（从0开始）扩展1个维度，负数代表从后开始数
        #具体到下面，就是先在第0维度上扩展成1*hidden_size*feature_size；
        # 然后.tile就是在第0维度复制batch_size次，变成batch_size*hidden_size*feature_size
        weight_ih_batch=weight_ih.unsqueeze(0).tile(batch_size,1,1)
     #   print("weight_ih_batch.shape", weight_ih_batch.shape)
        weight_hh_batch=weight_hh.unsqueeze(0).tile(batch_size,1,1)
     #   print("weight_hh_batch.shape", weight_hh_batch.shape)

        #计算两个tensor的矩阵乘法，torch.bmm(a,b),tensor a 的size为(b,h,w),tensor b的size为(b,w,m)
        # 也就是说两个tensor的第一维是相等的，然后第一个数组的第三维和第二个数组的第二维度要求一样，其实就是第一维不变，后面二维张量相乘，h*w*w*m=h*m
        # 对于剩下的则不做要求，输出维度 （b,h,m）
        # weight_ih_batch=batch_size*hidden_size*feature_size
        #x=batch_size*feature_size*1
        #w_times_x=batch_size*hidden_size*1
        ##squeeze，在给定维度（维度值必须为1）上压缩维度，负数代表从后开始数

        w_times_x=torch.bmm(weight_ih_batch,x).squeeze(-1)#
      #  print("w_times_x.shape", w_times_x.shape)

        w_times_h=torch.bmm(weight_hh_batch,h_prev.unsqueeze(2)).squeeze(-1)
      #  print("w_times_h.shape", w_times_h.shape)

        h_prev=torch.tanh(w_times_x+bias_ih+w_times_h+bias_hh)
        print("h_prev.shape", h_prev.shape)
        h_out[:,t,:]=h_prev
        print("h_out.shape", h_out.shape)

    return h_out,h_prev.unsqueeze(0)

if __name__=="__main__":
    # input=torch.randn(batch_size,T_seq,feature_size)
    # h_prev=torch.zeros(batch_size,hidden_size)

    # rnn=nn.RNN(input_size,hidden_size,batch_first=True)
    # output,state_final=rnn(input,h_prev.unsqueeze(0))

    # print(output)
    # print(state_final)
    batch_size, T_seq =10, 30  # 批大小，输入序列长度
    feature_size, hidden_size = 5, 8  #
    num_layers, output_size=1,3
    input = torch.randn(batch_size, T_seq, feature_size)
    h_prev = torch.zeros(1,batch_size, hidden_size)#.unsqueeze(0)
    # my_rnn=RNN(feature_size,hidden_size,num_layers,output_size)
    rnn=nn.RNN(feature_size,hidden_size,batch_first=True)
    # rnn_output, state_final = rnn(input, h_prev.unsqueeze(0))
    # for k,v in rnn.named_parameters():
    #     print(k,v.shape)
    my_rnn_output,my_state_final=rnn_forward(input,rnn.weight_ih_l0,rnn.weight_hh_l0,
                                             rnn.bias_ih_l0,rnn.bias_hh_l0,h_prev)
    print(my_rnn_output.shape)
    print(my_state_final.shape)

train.py

import torch
import torch.nn as nn
import numpy as np
#从自己创建的models库里导入RNN模块
#import RNN 仅仅是把RNN.py导入进来,当我们创建RNN的实例的时候需要通过指定RNN.py中的具体类.
#例如:我的RNN.py中的类名是RNN,则后面的模型实例化RNN需要通过**RNN.RNN()**来操作
#还可以通过 from 还可以通过 from RNN import * 直接把RNN.py中除了以 _ 开头的内容都导入
from models.nlp import RNN
from models.nlp.RNN import *

import datetime
import torch.optim as optim
#导入画图的库，后面将主要学习使用axes方法来画图
from matplotlib import pyplot as plt

batch_size=2#批大小
T_seq=30#输入序列长度(时间步）
feature_size=3#输入特征维度

hidden_size=5#隐含层维度
output_size=4#输出层维度

num_layers=1
lr_rate=0.001
epoch=1000
#input 即RNN网络的输入，维度应该为(T_seq, batch_size, input_size)。如果设置batch_first=True，输入维度则为(batch, seq_len, input_size)
input=torch.randn(batch_size,T_seq,feature_size)

def train(input):
    model=RNN(feature_size,hidden_size,num_layers,output_size)
    print("model:\n",model)
    # 设置损失函数
    loss_fn=nn.MSELoss()
    # 设置优化器
    optimizer=optim.Adam(model.parameters(),lr_rate)
    # 初始化h_prev，它和输入x本质是一样的，hidden_size就是它的特征维度
    #维度应该为(num_layers * num_directions, batch, hidden_size)。num_layers表示堆叠的RNN网络的层数。
    # 对于双向RNNs而言num_directions= 2，对于单向RNNs而言，num_directions= 1
    hidden_prev=torch.zeros(1,batch_size,hidden_size)
    loss_plt=[]
    #开始训练
    for iter in range(epoch):
        x = input
        print("x:", x.shape)

        output,hidden_prev=model(x,hidden_prev)
        print("output_size:",output.shape)
        #注意这里的标签，在实际任务的训练中标签往往是下一时刻的数据
        y = torch.randn(batch_size,T_seq,output_size)
        print("y:", y.shape)
        #返回一个新的tensor，从当前计算图中分离下来的，但是仍指向原变量的存放位置,
        # 不同之处只是requires_grad为false，得到的这个tensor永远不需要计算其梯度，不具有grad。
        hidden_prev=hidden_prev.detach()

        loss=loss_fn(output,y)
        model.zero_grad()
        loss.backward()
        optimizer.step()
        if iter%100==0:
            print("iteration:{} loss {}".format(iter,loss.item()))
            loss_plt.append(loss.item())

    fig,ax=plt.subplots(1,1)
    ax.plot(loss_plt, 'r')
    ax.set_xlabel('epcoh')
    ax.set_ylabel('loss')
    ax.set_title('RNN-train-loss')

    return hidden_prev, model

if __name__ == '__main__':
    #计算训练时间，结束时间减去开始时间
    start_time = datetime.datetime.now()
    hidden_pre, model = train(input)
    end_time = datetime.datetime.now()
    print('The training time: %s' % str(end_time - start_time))
    plt.show()