广义回归神经网络（General Regression Neural Network, GRNN）是一种基于径向基函数（Radial Basis Function, RBF）的神经网络模型，主要用于非线性回归任务。GRNN的主要特点是简单且易于实现，它能够快速地学习输入-输出映射关系，并且在处理噪声数据方面具有一定的鲁棒性。

GRNN的基本结构

GRNN通常包含四个层：

1. 输入层：接收输入数据。
2. 
3. 模式层：将隐藏层的输出标准化，使得每一行的输出之和为1。
4. 输出层：通过简单的线性组合从模式层获取输出。

GRNN的工作原理

当一个样本输入到网络时，隐藏层中的每一个节点都会计算该样本与自己中心向量之间的距离，并通过高斯函数计算出响应度。然后，在模式层将这些响应度标准化，最后在输出层通过加权平均获得最终的预测输出。

GRNN的优点

• 简单：相比于其他复杂的神经网络模型，GRNN的结构较为简单，易于理解和实现。
• 快速：由于不需要迭代训练过程，GRNN可以在很短的时间内构建好模型。
• 鲁棒性：对于含有噪声的数据集，GRNN依然能给出较好的预测结果。

GRNN的局限性

• 过拟合风险：如果标准差（spread）选择不当，可能会导致过拟合。
• 泛化能力有限：相比于深度学习模型，GRNN的泛化能力可能较弱。

如何使用GRNN

在MATLAB中，你可以使用 newgrnn 函数来创建一个GRNN。这个函数接受输入数据矩阵 P 和目标数据矩阵 T，以及一个标准差参数 spread。标准差的选择非常重要，它决定了模型的平滑程度。

%%   训练速度快 非线性映射能力强   常用于函数逼近
clear all;
close all;
P=1:30;
T=3*sin(P);
net=newgrnn(P,T,0.3);      %径向基函数的分布密度是0.3
y=sim(net,P);
figure;
plot(P,T,':+',P,T-y,'-o');

代码解释

1. 生成输入数据：

    

   P = 1:30;

   生成一个从 1 到 30 的向量，作为输入数据。

2. 生成目标输出：

   T = 3 * sin(P);

   生成一个正弦波函数 3 * sin(P) 作为目标输出。

3. 创建 GRNN 网络：

   net = newgrnn(P, T, 0.3);

   使用 newgrnn 函数创建一个 GRNN 网络，其中 0.3 是径向基函数的标准差（spread），表示径向基函数的分布密度。

4. 模拟网络输出：

   y = sim(net, P);

   使用创建好的 GRNN 网络对输入数据 P 进行模拟，得到预测输出 y。

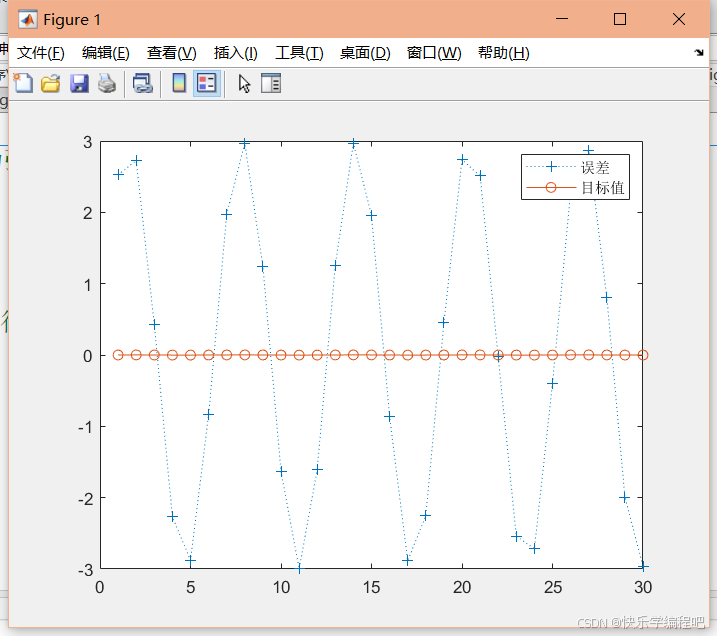
5. 绘制结果：

   figure;
   plot(P, T, ':+', P, T - y, '-o');

   绘制实际输出 T 和误差 T - y 的曲线。