在实现神经网络算法时，会遇到如何判断反向传播求解的梯度是否正确的问题，对于梯度的检验在进行梯度下降前完成，在进行梯度下降时一定不要进行该操作，这样会浪费内存。

对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的 θ，我们计算出在 θ-ε 处和 θ+ε 的代价值（ε是一个非常小的值，通常选取 0.001），然后求两个代价的平均，用以估计在 θ 处的代价值。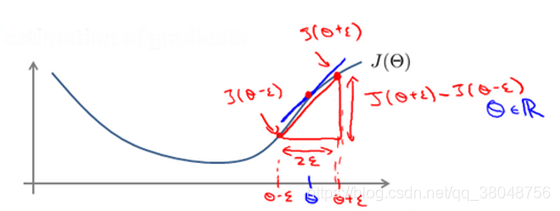

当θ是一个向量时，我们则需要对偏导数进行检验。因为代价函数的偏导数检验只针对一个参数的改变进行检验，下面是一个只针对θ_1进行检验的示例：

最后我们还需要对通过反向传播方法计算出的偏导数计算出的偏导数存储在矩阵 D_ij^(l)中。检验时，我们要将该矩阵展开成为向量，同时我们也将 θ 矩阵展开为向量，我们针对每一个 θ 都计算一个近似的梯度值，将这些值存储于一个近似梯度矩阵中，最终将得出的这个矩阵同 D_ij^(l)进行比较。