---

CNN（卷积神经网络）详解

视觉处理三大任务：图像分类、目标检测、图像分割
上游：提取特征，CNN’
下游：分类、目标、分割等，具体的业务

1. 概述

• 卷积神经网络（CNN） 是深度学习在计算机视觉领域的突破性成果。 在计算机领域，往往我们输入的图像都很大，使用全连接网络的话，计算的代价较高，另外图像也很难保留原有的特征，导致图像处理的准确率不高。
• 卷积神经网络（Convolutional Neural Network, CNN）是一种专门处理具有网格状态结构数据的深度学习模型。最初，CNN主要应用于计算视觉任务，但它的成功启发了在其他领域应用，如自然语言处理等。
• 卷积神经网络（Convolutional Neural Network）是含有卷积层的神经网络，卷积层的作用就是用来自动学习，提取图像的特征
• CNN网络主要有三部分构成：卷积层、池化层和全连接层构成，其中卷积层负责提取图像中的局部特征；池化层用来大幅降低运算量并特征增强；全连接层类似神经网络的部分，用来输出想要的结果。

1.1 使用场景

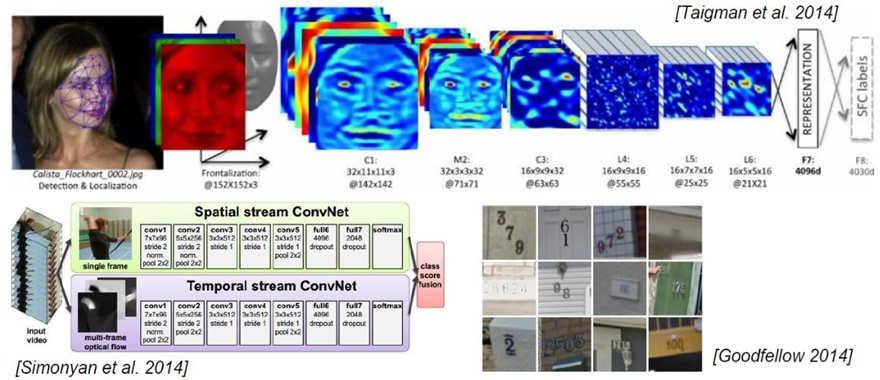
1.2 与传统网络的区别

• 结构上区别：
  -传统神经网络传统神经网络对输入数据的结果没有明确的处理要求，适用于线性数据，如结构化数据的分类任务
  卷积神经网络每个神经元只与前一层的一部分神经元相连接，主要依赖局部连接、权重共享和池化操作。CNN主要用于处理具有空间结构的数据

• 参数共享与局部连接：
  -传统神经网络每一层的每个神经元都会连接到上一层的所有神经元，这样会产生大量的参数，尤其在处理大规模数据时，计算开销巨大
  CNN通过卷积层实现局部连接和参数共享。卷积操作让每个卷积核只关注输入数据的一部分区域，从而减少了模型参数的数量

• 提取特征方式：
  传统神经网络特征提取完全依赖于输入特征的手工设计。特征工程质量直接影响模型的表现
  CNN通过卷积层自动提取数据中的局部特征，从低级到高级逐步学习，不需要手动提取特征。

• 适用数据类型不同：
  传统神经网络主要适用于结构化数据，如表格数据或时序数据，依赖于输入的特征空间
  CNN主要用于图像、视屏、语音等具有空间结构或时序结构的数据。CNN能够自动学习数据中的空间层次结构特征，不需要手动提取特征

• 计算效率：
  传统神经网络由于是全连接层，每一层都需要计算大量的连接权重，计算效率较低，尤其是处理图像数据时
  CNN通过卷积操作局部连接，并且采用权重共享，大大减少了计算量

• 适用问题的不同：
  传统神经网络适合处理不具备空间结构的数据
  CNN特别适用于具有空间结构的数据（如图像、视频、音频），并且在图像识别、目标检测、语音识别等领域表现优异。

1.3 全连接的局限性

参数量过大，计算成本高，容易过拟合（惨数量庞大，模型容量过强，容易在小数据上过拟合，需要大量数据，正则化，早停等手段来缓解），无法捕捉局部特征，可解释性差，泛化能力不足，训练难度大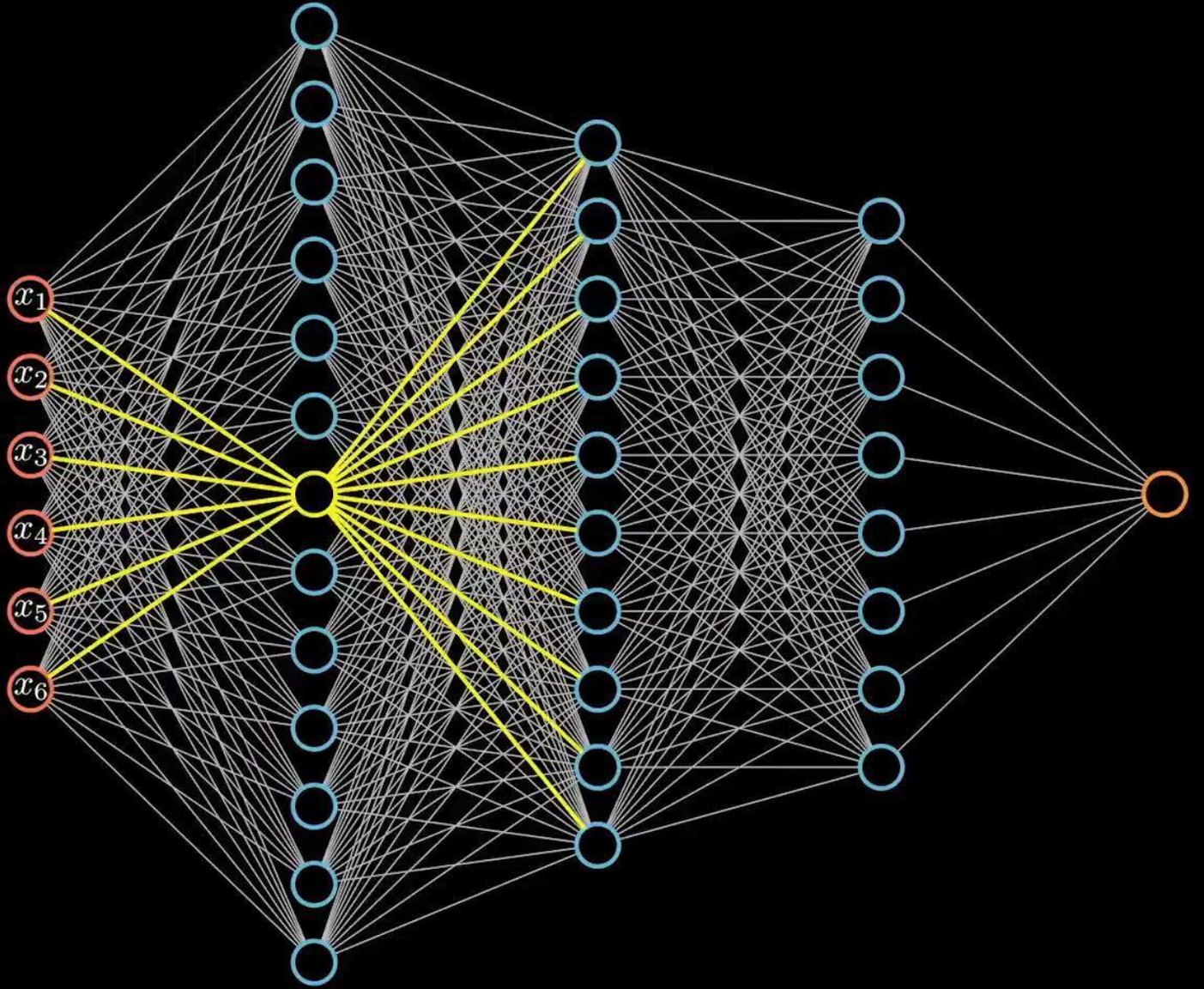

2. 卷积层（Convolutional Layer）

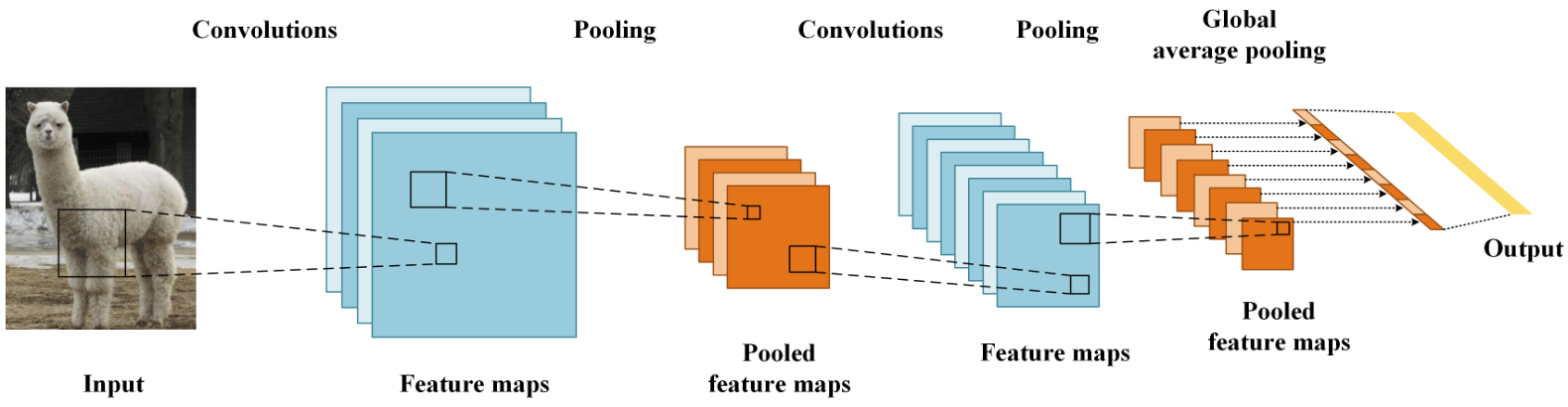
• 卷积操作：通过卷积核（滤波器）与输入数据进行卷积，提取特征。

  • 卷积的本质是滑动窗口操作。

• 卷积层的作用：从输入数据中学习空间特征。通常，卷积层会逐渐学习从低级到高级的特征。

• 卷积核（滤波器）：
  卷积核在卷积运算中是必不可少的，被用来提取图像中的特征。卷积核就是一个小“矩阵”，在定义时需要考虑以下几方面内容：

  • 卷积核个数：卷积核（过滤器）的个数决定了其输出特征矩阵的通道数
  • 卷积核的值：卷积核的值是初始化好的，后续进行更新
  • 卷积核的大小：一般都是奇数，如：

2.1 卷积计算过程

卷积的过程是将卷积核在图像上进行滑动计算，每次滑动到一个新的位置时，卷积核和图像进行点对点的计算，并将其求和得到一个新的值，然后将这个新的值加入到特征图中，最终得到一个新的特征图。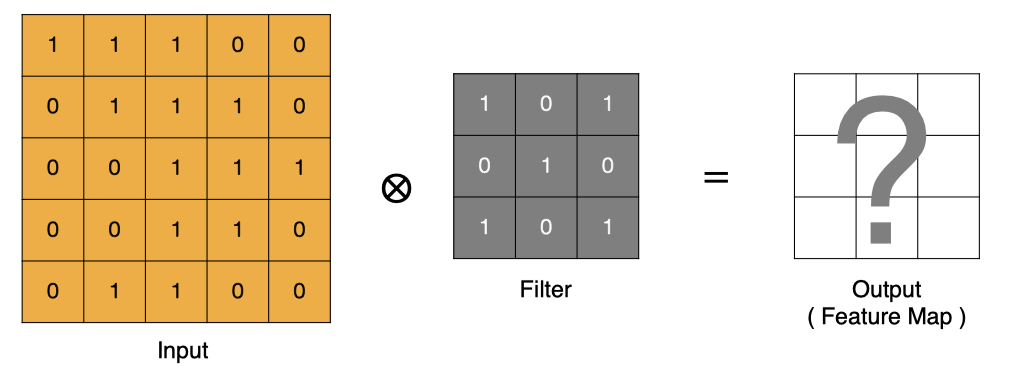

1. input 表示输入的图像
2. filter 表示卷积核, 也叫做滤波器
3. input 经过 filter 的得到输出为最右侧的图像，该图叫做特征图

​ 那么, 它是如何进行计算的呢？卷积运算本质上就是在滤波器和输入数据的局部区域间做点积。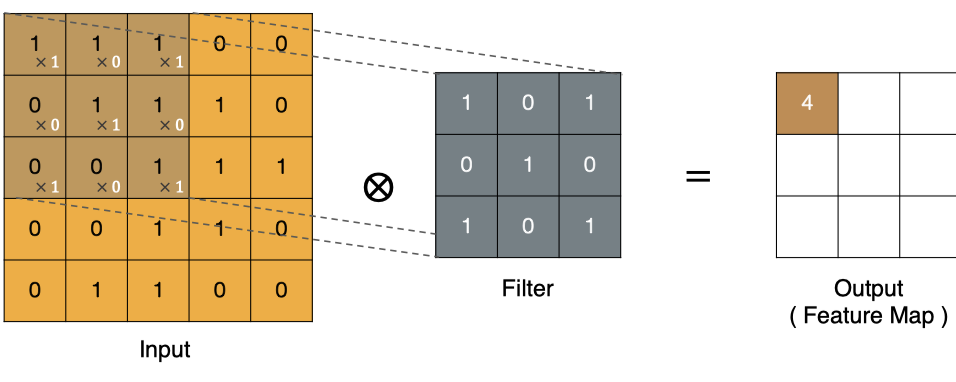

左上角的点计算方法：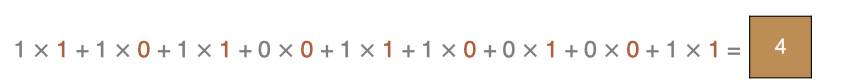

按照上面的计算方法可以得到最终的特征图为: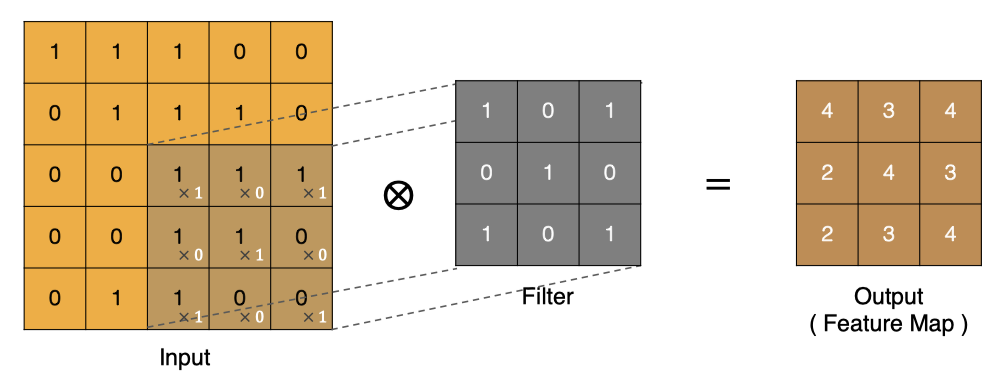
卷积的重要性在于它可以将图像中的特征与卷积核进行卷积操作，从而提取出图像中的特征。
可以通过不断调整卷积核的大小，卷积核的值和卷积操作的步长，可以提取出不同尺度和位置的特征。

2.2 卷积计算底层实现

并不是水平和垂直方向的循环
下图是卷积的基本运算方式：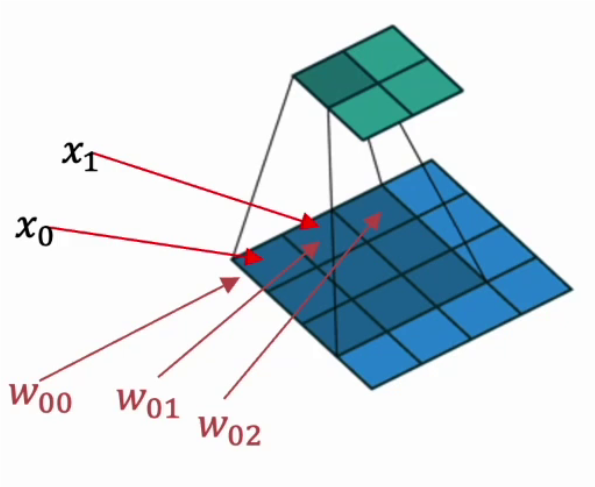
卷积真正的计算过程如下图：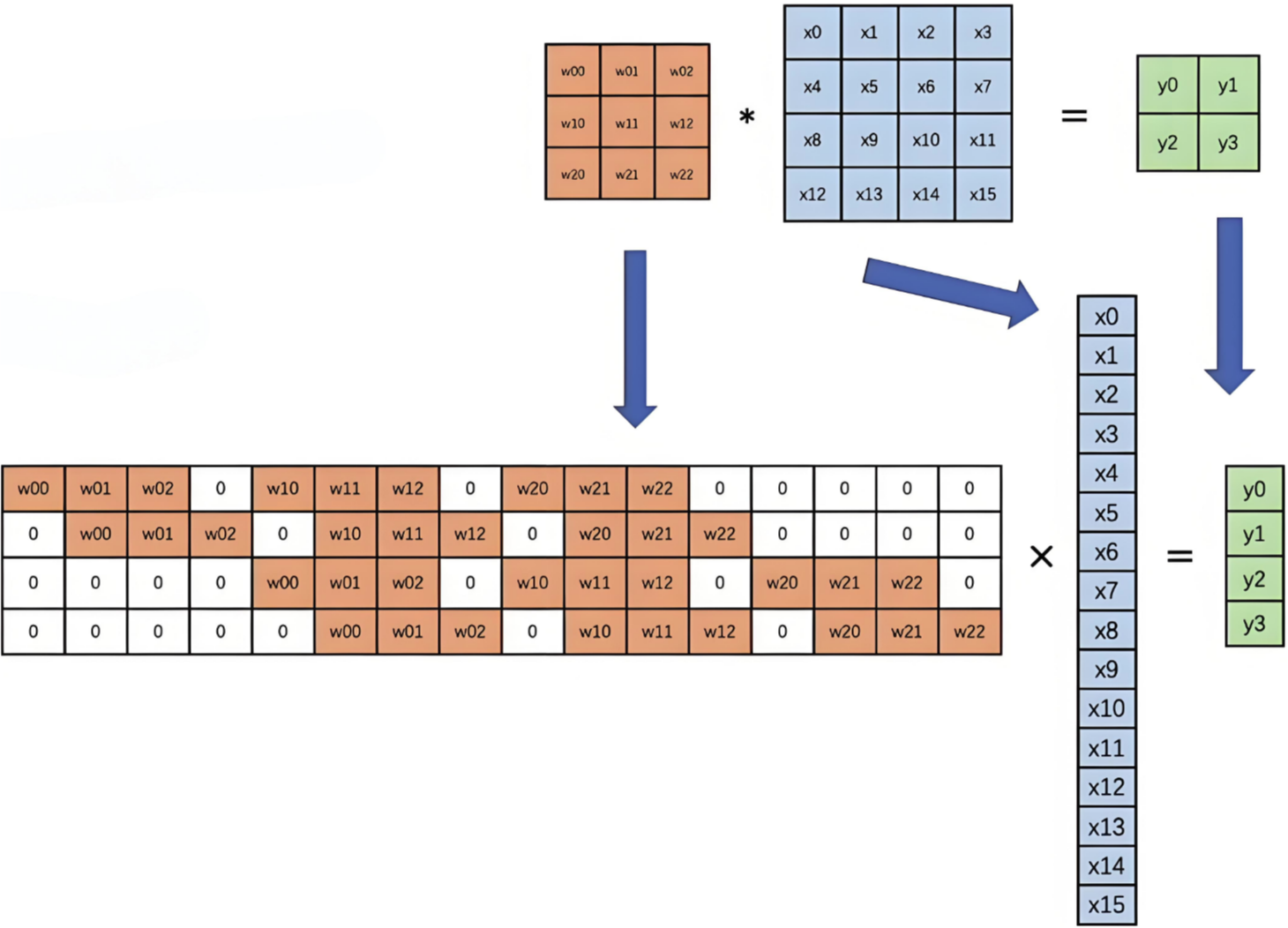

2.3 边缘填充

Padding,通过上面的卷积计算，我们发现最终的特征图比原始图要小，如果想要保持图像大小不变，可在原图周围添加padding来实现
更重要的，边缘填充更好的保护了图像边缘数据的特征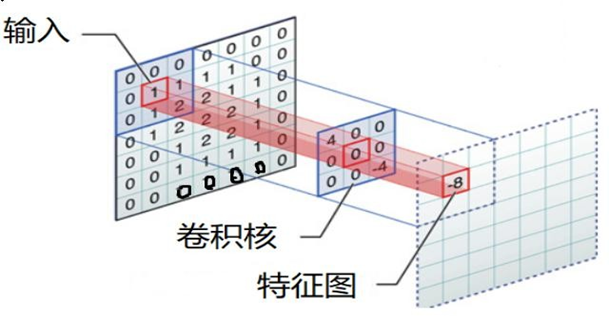

2.4 步长Stride

按照步长为1来移动卷积核，计算特征图如下所示：

Stride 增大为2，也是可以提取特征图的，如下图所示：

stride太小：重复计算较多，计算量大，训练效率降低；
stride太大：会造成信息遗漏，无法有效提炼数据背后的特征；
特征图输出大小：

2.5 卷积参数共享

​ 数据是 $32\times 32\times 3$ 的图像，用 $10$ 个 $5\times 5$ 的filter来进行卷积操作，所需的权重参数有多少个呢？

• $5\times 5\times 3=75$，表示每个卷积核只需要$75$个参数。
• 10个不同的卷积核，就需要$10\ast 75=750$个卷积核参数。
• 如果还考虑偏置参数$b$，最终需要 $750+10=760$ 个参数。
  $$全连接参数量：10\ast 28\ast 28\ast (32\ast 32\ast 3+1)$$

3. 池化层（Pooling Layer）

3.1 概述

池化层(Pooling)降低空间维度，缩减模型大小，提高计算速度，即：主要对卷积层学习到的特征图进行下采样（SubSampling）处理

• 1. 最大池化 max pooling
  最大池化是从每个局部区域中选择最大值作为池化后的值，这样可以保留局部区域中最显著的特征。最大池化在提取图像中的纹理、形状等方面具有很好的效果。

• 2. 平均池化 avgPooling
  平均池化是将局部区域中的值取平均作为池化后的值，这样可以得到整体特征的平均值。平均池化在提取图像中的整体特征、减少噪声等方面具有较好的效果。

• 作用：减少空间维度（宽高），降低计算量，同时保留重要的特征。
• 池化操作通常是在每个卷积层后面进行，用于缩小输入的尺寸，提高特征的抽象级别。

3.2 池化层计算

整体结构：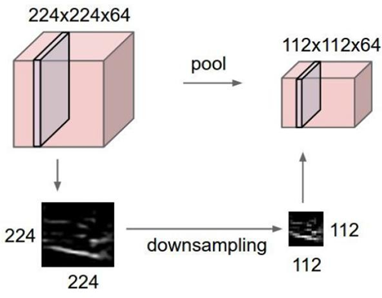
计算：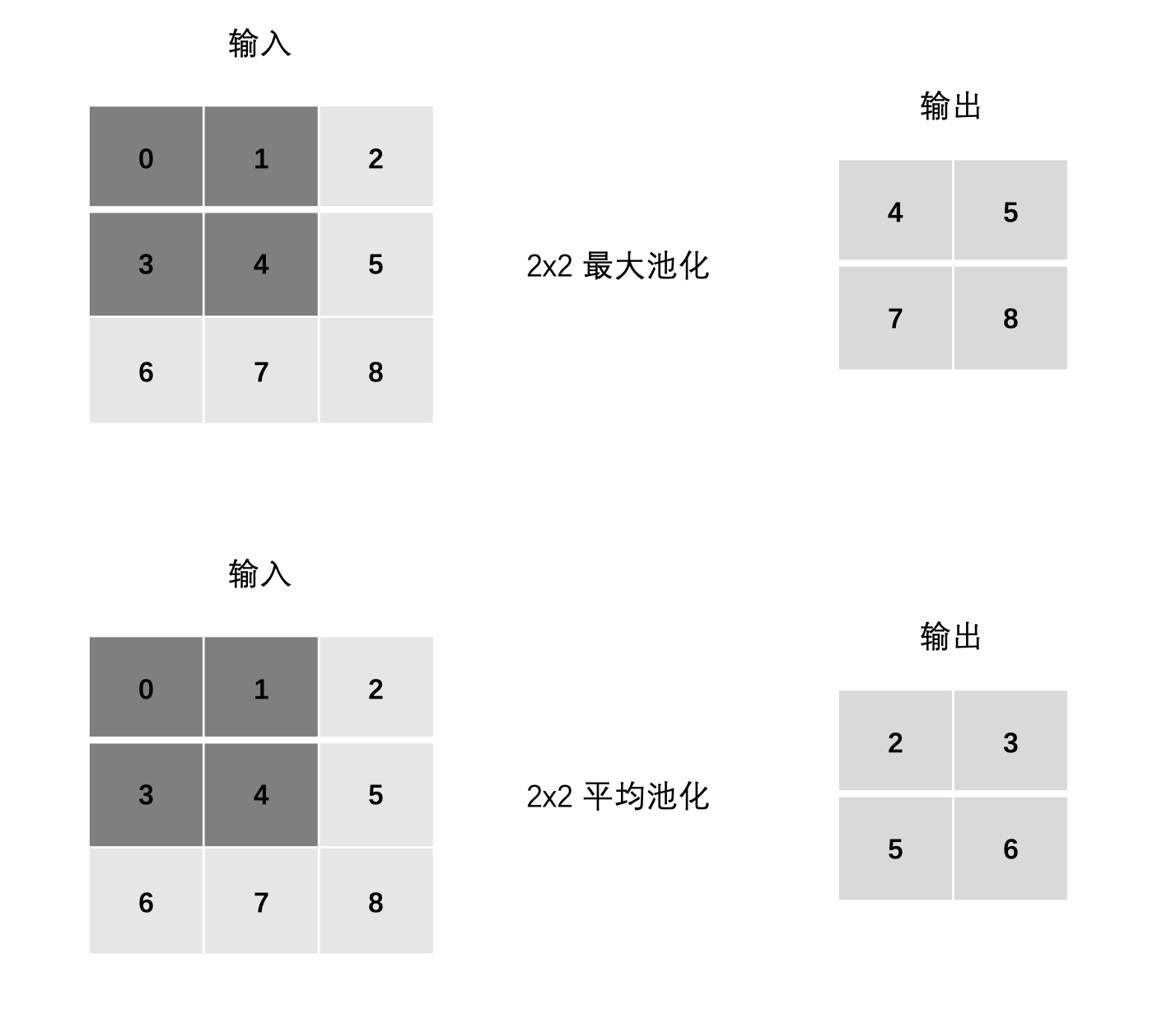
最大池化:

1. max(0, 1, 3, 4)
2. max(1, 2, 4, 5)
3. max(3, 4, 6, 7)
4. max(4, 5, 7, 8)

平均池化:

1. mean(0, 1, 3, 4)
2. mean(1, 2, 4, 5)
3. mean(3, 4, 6, 7)
4. mean(4, 5, 7, 8)

4. 整体结构

• CNN 网络的典型结构：由多个卷积层、池化层交替堆叠，再接上若干全连接层（Fully Connected Layer）。
• 结构示意：
  输入图像 → 卷积层 → 激活函数 → 池化层 → 卷积层 → 池化层 → 全连接层 → 输出。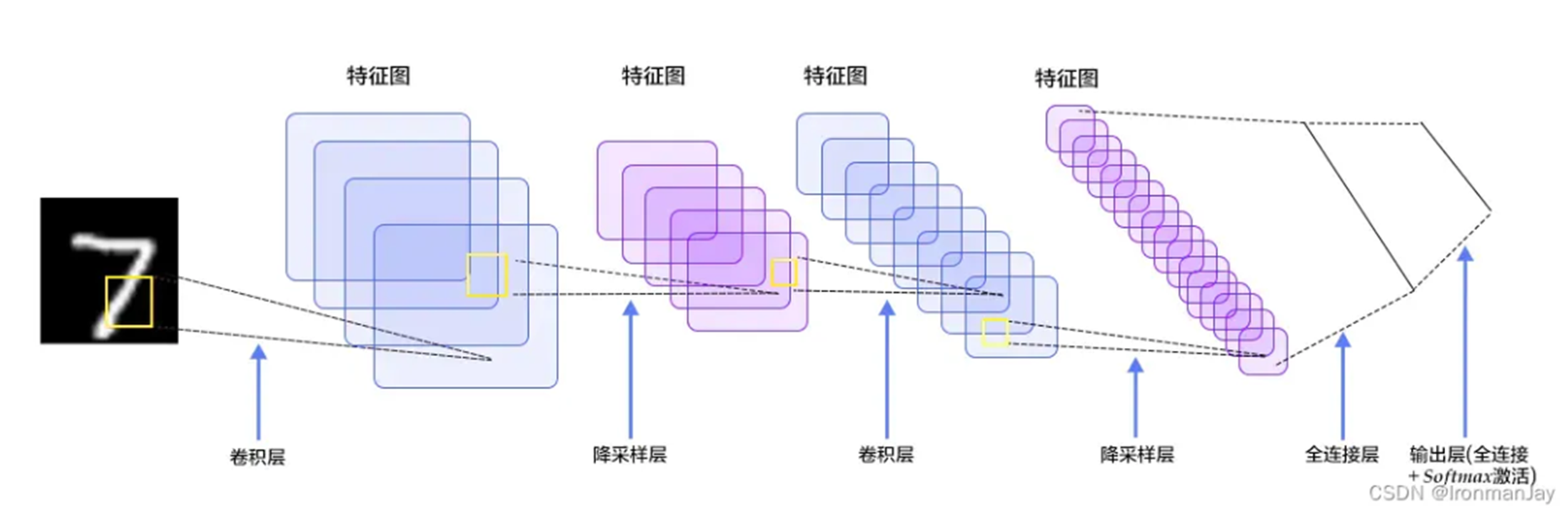
  

5. 卷积知识扩展

• 卷积操作的数学原理：
  卷积是数学中一种函数运算，用于提取图像局部特征。

  • 数学表示：

    $$I_{out}(x,y)=(I\ast K)(x,y)=\sum _m\sum _{n}I(m,n)\cdot K(x-m,y-n)$$

    其中，$I$ 是输入图像，$K$ 是卷积核，* 表示卷积操作。

• 边缘检测与卷积：常用的卷积核如 Sobel、Prewitt 用于图像边缘检测。

5.1 深度可分离卷积的思想

将卷积分解为 两步：

(1) Depthwise Convolution（逐通道卷积）

• 每个输入通道只用一个卷积核 $K\times K$，不与其他通道混合。
• 作用：提取每个通道的空间特征。

参数量公式：

$$Para{m}_{DW}=C_{in}\times K\times K$$

---

(2) Pointwise Convolution（逐点卷积）

• 使用 $1\times 1$ 卷积，对逐通道卷积的结果进行 通道融合。
• 作用：实现不同通道之间的信息交互。

参数量公式：

$$Para{m}_{PW}=C_{in}\times C_{out}$$

---

(3) 总参数量

$$Para{m}_{DSC}=C_{in}\times K\times K+C_{in}\times C_{out}$$

与标准卷积相比，参数量 大幅下降。

6. 感受野（Receptive Field）

• 感受野定义：感受野是卷积层神经元能感知的输入区域大小。卷积神经网络通过增加感受野来获取全局特征。

• 如何增加感受野：

  • 增加卷积核的尺寸。
  • 使用多个卷积层。
  • 通过池化层增大感受野。

根据这个结构，你可以在每个部分填充相应的细节内容。例如，卷积层部分可以深入讲解卷积核的选择、步长和填充的作用；在卷积神经网络案例中，可以包括代码实现、模型训练等内容。希望这个结构对你有所帮助！