Title

题目

Recurrent inference machine for medical image registration

医学图像配准的循环推理机

01

文献速递介绍

医学图像配准相关研究内容翻译 医学图像配准是指在两幅或多幅医学图像间建立解剖学对应关系的过程，该技术在医学影像研究中应用广泛，涵盖影像特征融合（Haskins 等人，2020；Oliveira 与 Tavares，2014）、治疗方案制定（Staring 等人，2009；King 等人，2010；Byrne 等人，2022）以及患者纵向研究（Sotiras 等人，2013；Jin 等人，2021）等领域。 传统上，医学图像配准被构建为一个优化问题，旨在通过迭代方式求解参数化变换（Klein 等人，2007）。通常，优化目标包含两部分：一是用于实现图像间对齐的相似性项，二是用于施加平滑约束的正则化项。由于非凸优化问题的复杂性，传统方法往往存在运行时间长的问题，对于大型高分辨率图像而言尤为明显。这一缺陷使其在临床实践中的实际应用受到限制，例如在手术导航（Sauer，2006）场景中，临床需求要求图像配准具备快速性（Avants 等人，2011；Balakrishnan 等人，2019）。 随着机器学习技术的近期发展，数据驱动的深度学习范式在医学图像配准领域逐渐受到青睐（Rueckert 与 Schnabel，2019）。与传统优化流程通过迭代更新变换参数不同，基于深度学习的配准方法能够在推理阶段快速实现从图像到变换的预测。早期相关研究通过有监督学习方式学习变换（Miao 等人，2016；Yang 等人，2016），随后无监督学习方法逐渐成为主流。这些无监督方法采用与传统方法类似的损失函数，但通过摊销神经网络对其进行优化（Balakrishnan 等人，2019；De Vos 等人，2019）。这些研究充分证明了基于深度学习的模型在医学图像配准领域的巨大潜力。然而，与迭代方法相比，图像变换的一步式推理本质上是一项极具挑战性的任务，尤其是在形变场较大的情况下。在实际应用中，一步式推理需要相对大量的数据来训练深度学习网络，以实现稳定预测，且在推理阶段仍可能产生不符合预期的变换结果（Fechter 与 Baltas，2020；Hering 等人，2019；Zhao 等人，2019）。 与一步式推理不同，近年来有研究重新采用迭代式配准方法，通过多步推理流程实现配准（Fechter 与 Baltas，2020；Kanter 与 Lellmann，2022；Qiu 等人，2022；Sandkühler 等人，2019；Zhao 等人，2019）。其中部分迭代方法（Kanter 与 Lellmann，2022；Qiu 等人，2022）属于元学习范畴。元学习的核心并非学习优化后的参数，而是聚焦于学习优化过程本身。Andrychowicz 等人（2016）与 Finn 等人（2017）将元学习应用于图像分类任务的优化过程中，结果表明该方法能够提升模型的泛化能力并加快收敛速度。在医学影像应用领域，一个典型案例是 Putzky 与 Welling（2017）提出的循环推理机（RIM），该模型最初被设计用于求解带有显式正向物理模型的逆问题，现已在快速磁共振成像（MRI）重建（Lønning 等人，2019）和磁共振弛豫测量（Sabidussi 等人，2021）任务中展现出优异性能。 在本研究中，我们提出了一种新型元学习医学图像配准方法，名为循环推理图像配准（RIIR）网络。该网络的设计灵感来源于循环推理机（RIM），但对其概念进行了显著扩展，以解决更具通用性的优化问题：与逆问题不同，医学图像配准面临的是高维优化挑战，且不存在闭式正向模型。下文将通过详细综述，阐明本研究的设计动机。  ## 1.1 相关研究 本节将对基于深度学习的医学图像配准方法进行详细综述，并将其分为用于直接图像-变换推理的一步式方法和用于多步推理的迭代式方法两类。此外，还将简要概述元学习在医学影像应用中的相关研究。 ### 1.1.1 基于深度学习的一步式配准 早期利用卷积神经网络（CNN）实现医学图像配准的研究，仅支持有限类型的变换，例如 SVF-Net（Rohé 等人，2017）、Quicksilver（Yang 等人，2017）以及 Cao 等人（2017）的研究成果，这些方法大多采用有监督学习方式进行训练。随着 U-Net 架构（Ronneberger 等人，2015）的提出——该架构凭借多分辨率特性和跳跃连接具备出色的空间表达能力——Balakrishnan 等人（2019）、Dalca 等人（2019）以及 Hoopes 等人（2021）相继提出了无监督可变形配准框架。De Vos 等人（2019）的研究进一步考虑了仿射变换与可变形变换的结合。近年来，相关方法通过采用不同的神经网络骨干网络（如Transformer（Zhang 等人，2021）或隐式神经表示（Wolterink 等人，2022；van Harten 等人，2023）），对配准框架进行了扩展。 ### 1.1.2 基于深度学习的迭代式配准 然而，在预测大规模复杂变换时，一步式推理策略可能难以应对（Hering 等人，2019；Zhao 等人，2019）。与基于深度学习的一步式配准方法不同，近年来的研究采用迭代流程，从图像分辨率（Hering 等人，2019；Mok 与 Chung，2020；Fechter 与 Baltas，2020；Xu 等人，2021；Liu 等人，2021）、多轮优化步骤（Zhao 等人，2019；Sandkühler 等人，2019；Falta 等人，2022；Kanter 与 Lellmann，2022）或两者结合（Qiu 等人，2022）等角度，重现了医学图像配准的传统优化流程。 Sandkühler 等人（2019）的研究考虑采用带有门控循环单元（GRU）的循环神经网络（RNN）（Chung 等人，2014），在该方法中，每一步都会通过添加一个独立的参数化变换来逐步更新配准变换。Zhao 等人（2019）提出的另一种多步式方法，利用递归级联网络生成一系列变换，再通过组合这些变换得到最终的配准变换。但该方法需要为每一步推理设置独立模块，存在内存效率低的问题。 Hering 等人（2019）提出了一种基于不同分辨率层级的变分方法，其中最终变换是由粗粒度到细粒度变换的组合结果。Fechter 与 Baltas（2020）的研究通过评估数据可用性有限且存在较大域偏移时的模型性能，强调了基于深度学习的模型在数据效率方面的重要性。Falta 等人（2022）提出了一种名为“学习优化（L2O）”的迭代式方法，用于在肺部计算机断层扫描（CT）配准任务中模拟基于梯度的优化过程。该方法摒弃了完全无监督的训练模式，而是通过对生成的关键点采用深度监督策略，并循环使用 U-Net 网络进行训练。值得注意的是，该方法还引入了额外的输入特征模态（包括动态采样坐标和 MIND 特征（Heinrich 等人，2012））以增强模型性能。 Qiu 等人（2022）近期提出的“图像配准梯度下降网络（GraDIRN）”，将多步推理与多分辨率特性整合到医学图像配准中。具体而言，该方法的更新规则借鉴了传统优化思想：通过求解相似性项相对于当前变换的梯度，并利用 CNN 估计正则化项的梯度，进而实现变换更新。尽管研究表明，与 CNN 输出相比，梯度项的直接影响较小（Qiu 等人，2022），但该方法成功搭建了基于梯度的优化方法与基于深度学习的配准方法之间的桥梁。 Kanter 与 Lellmann（2022）提出的方法则采用独立的长短期记忆（LSTM）模块实现变换的循环优化，但该研究的应用范围仅限于仿射变换，而仿射变换在传统医学图像配准流程中仅作为初始化步骤使用。 ### 1.1.3 元学习与循环推理机 元学习，也被称为“学会学习（learning to learn）”，是机器学习的一个子领域。在该方法中，外层算法会对内层学习算法进行更新，使模型能够调整并优化自身的学习策略，从而实现更广泛的目标。例如，在元学习场景中，可在多种任务（如不同类型的图像识别任务）上训练模型，目标是让模型仅通过少量训练样本，就能快速适应未见过的相似任务（如识别原始训练集中未包含的新物体类别）（Hospedales 等人，2021）。 元学习的早期研究方向是设计能够根据不同任务和数据输入更新自身参数的网络架构（Schmidhuber，1993）。Cotter 与 Conwell（1990）以及 Younger 等人（1999）的研究进一步表明，固定权重的循环神经网络（RNN）在学习多项任务时具有灵活性。近年来，Andrychowicz 等人（2016）、Chen 等人（2017）以及 Finn 等人（2017）开发并研究了利用 RNN 学习优化过程的方法，结果表明该类方法在未见过的任务上具有更快的收敛速度和更优的泛化能力。 基于元学习思想，Putzky 与 Welling（2017）开发了循环推理机（RIM），用于求解逆问题。RIM 学习一种单一的循环架构，该架构在所有迭代步骤中共享参数，且内部状态会在迭代过程中传递（Putzky 与 Welling，2017）。在元学习背景下，RIM 区分了两个不同层级的任务：“内层任务”聚焦于求解特定的逆问题（如图像超分辨率重建），“外层任务”则旨在优化优化过程本身。这种设定使 RIM 能够高效学习并将优化策略应用于复杂问题，因此，RIM 仅需一个神经网络组件即可完成外层任务的学习。 目前，RIM 已在多个应用领域展现出稳健且具竞争力的性能，从宇宙学（Morningstar 等人，2019；Modi 等人，2021）到医学影像（Karkalousos 等人，2022；Lønning 等人，2019；Putzky 等人，2019；Sabidussi 等人，2021、2023）均有涉及。据我们所知，RIM 的大多数应用旨在求解具有闭式可微正向模型的逆问题，例如在 MRI 重建中结合灵敏度图和采样掩码的傅里叶变换（Lønning 等人，2019）。 然而，医学图像配准任务并不存在显式正向模型的定义。尽管 RIM 的设计本身不要求必须有正向模型，但缺乏具体的正向模型会使问题变得更为复杂。在这种情况下，我们的模型构建方式与迭代式摊销推理（Marino 等人，2018）的实现思路相似。Marino 等人（2018）的研究中，在特定正向模型下似然函数可能缺失的情况下，通过变分自编码器（VAE）框架学习基于输入数据和近似后验梯度的摊销优化过程。 本研究旨在将循环推理机（RIM）框架扩展到医学图像配准问题中——RIM 已在医学图像重建挑战赛中展现出最先进的性能（Muckley 等人，2021；Putzky 等人，2019；Zbontar 等人，2018），而扩展后的框架无需依赖特定正向模型下的梯度似然函数。该框架还可推广到其他高维优化问题，即不存在显式正向模型但具备可微评估指标的问题。  ## 1.2 研究贡献 本研究的主要贡献体现在以下三个方面： 1. 提出了一种用于医学图像配准的新型元学习框架 RIIR。该框架在缺乏显式正向模型的情况下，能够学习优化过程；同时，RIIR 对输入模态具有良好的适应性，且在不同医学图像配准应用中均展现出具有竞争力的精度。 2. 与现有基于深度学习的迭代式方法不同，本方法将输入图像的梯度信息整合到密集增量变换的预测过程中。由此，与一步式推理相比，RIIR 大幅简化了学习任务，实验结果也证明该方法显著提升了整体数据效率。 3. 通过深入的消融实验，不仅验证了所提方法在不同输入选择下的灵活性，还探究了循环推理机（RIM）框架内不同架构选择对模型性能的影响。尤其值得注意的是，本研究证实了在医学影像场景下求解复杂优化问题时，隐藏状态具有额外价值——这一问题在现有文献中尚未得到充分探索。

Abatract

摘要

Image registration is essential for medical image applications where alignment of voxels across multiple imagesis needed for qualitative or quantitative analysis. With recent advances in deep neural networks and parallelcomputing, deep learning-based medical image registration methods become competitive with their flexiblemodeling and fast inference capabilities. However, compared to traditional optimization-based registrationmethods, the speed advantage may come at the cost of registration performance at inference time. Besides,deep neural networks ideally demand large training datasets while optimization-based methods are trainingfree. To improve registration accuracy and data efficiency, we propose a novel image registration method,termed Recurrent Inference Image Registration (RIIR) network. RIIR is formulated as a meta-learning solverfor the registration problem in an iterative manner. RIIR addresses the accuracy and data efficiency issues, bylearning the update rule of optimization, with implicit regularization combined with explicit gradient input.We extensively evaluated RIIR on brain MRI, lung CT, and quantitative cardiac MRI datasets, in termsof both registration accuracy and training data efficiency. Our experiments showed that RIIR outperformeda range of deep learning-based methods, even with only 5% of the training data, demonstrating high dataefficiency. Key findings from our ablation studies highlighted the important added value of the hiddenstates introduced in the recurrent inference framework for meta-learning. Our proposed RIIR offers a highlydata-efficient framework for deep learning-based medical image registration

医学图像配准相关研究内容翻译 图像配准对于医学图像应用至关重要。在这类应用中，为开展定性或定量分析，需对多幅图像间的体素进行对齐。随着深度神经网络与并行计算技术的近期发展，基于深度学习的医学图像配准方法凭借其灵活的建模能力和快速的推理性能，已具备较强的竞争力。然而，与传统的基于优化的配准方法相比，其速度优势的获取可能以牺牲推理阶段的配准性能为代价。此外，深度神经网络理想情况下需要大规模训练数据集，而基于优化的方法则无需训练。 为提升配准精度与数据效率，我们提出了一种新型图像配准方法，称为循环推理图像配准（RIIR）网络。该网络将配准问题构建为元学习求解器，通过迭代方式进行求解。RIIR网络通过学习优化更新规则，并结合隐式正则化与显式梯度输入，解决了精度与数据效率方面的问题。 我们在脑部磁共振成像（MRI）、肺部计算机断层扫描（CT）以及定量心脏磁共振成像数据集上，从配准精度和训练数据效率两方面对RIIR网络进行了全面评估。实验结果表明，即便仅使用5%的训练数据，RIIR网络仍优于多种基于深度学习的方法，展现出较高的数据效率。消融实验的关键发现表明，在用于元学习的循环推理框架中引入隐藏状态，具有重要的附加价值。我们提出的RIIR网络为基于深度学习的医学图像配准提供了一个数据效率极高的框架。

Method

方法

2.1. Deformable image registration

Deformable image registration aims to align a moving image 𝐼movto a fixed image 𝐼fix by determining a transformation 𝝓 acting onthe shared coordinates 𝝌, such that the transformed image 𝐼mov◦𝝓 issimilar enough to 𝐼fix. The similarity is often evaluated by a scalarvalued metric. In deformable image registration, 𝝓 is considered tobe a relatively small displacement added to the original coordinate 𝝌,expressed as 𝝓 = 𝝌 + 𝑢(𝝌). Since the transformation 𝝓 is calculatedbetween the pair (𝐼mov, 𝐼fix), the process is often referred to as pairwiseregistration (Balakrishnan et al., 2019). Finding such transformation 𝝓in pairwise registration can be viewed as the following optimizationproblem:

𝝓*̂ = argmin𝝓sim (𝐼mov◦𝝓, 𝐼fix) + 𝜆reg (𝝓), (1)

where sim is a similarity term between the deformed image 𝐼mov◦𝝓and fixed image 𝐼fix, reg is a regularization term constraining 𝝓, and𝜆* is a trade-off weight term

2.1 可变形图像配准 可变形图像配准旨在通过确定作用于公共坐标𝝌的变换𝝓，将浮动图像𝐼mov与固定图像𝐼fix对齐，使得变换后的图像𝐼mov◦𝝓与𝐼fix足够相似。这种相似性通常通过一个标量值度量来评估。在可变形图像配准中，𝝓被视为在原始坐标𝝌基础上叠加的一个相对较小的位移，表达式为𝝓=𝝌+𝑢(𝝌)（其中𝑢(𝝌)为位移场）。由于变换𝝓是基于图像对（𝐼mov, 𝐼fix）计算得到的，因此该过程通常被称为“成对配准”（pairwise registration）（Balakrishnan 等人，2019）。 在成对配准中，寻找上述变换𝝓的问题可转化为如下优化问题： 𝝓*̂ = argmin𝝓 sim(𝐼mov◦𝝓, 𝐼fix) + 𝜆reg(𝝓)  (1) 其中，sim表示变形后图像𝐼mov◦𝝓与固定图像𝐼fix之间的相似性项，reg表示对变换𝝓施加约束的正则化项，𝜆为平衡两项权重的trade-off系数。

Conclusion

结论

In conclusion, we present RIIR, a novel recurrent deep-learningframework for medical image registration. RIIR significantly extendsthe concept of recurrent inference machines for inverse problem solving, to high-dimensional optimization challenges with no closed-formforward models. Meanwhile, RIIR distinguishes itself from previousiterative methods by integrating implicit regularization with explicitloss gradients. Our experiments across diverse medical image datasetsdemonstrated RIIR’s superior accuracy and data efficiency. We alsoempirically demonstrated the effectiveness of its architectural designand the value of hidden states, significantly enhancing both registrationaccuracy and data efficiency. RIIR is shown to be an effective and generalizable tool for medical image registration, and potentially extendsto other high-dimensional optimization problems.

本研究提出了一种用于医学图像配准的新型循环深度学习框架——RIIR（循环推理图像配准网络）。该框架将用于求解逆问题的循环推理机（RIM）概念进行显著扩展，使其能够应对无闭式正向模型的高维优化挑战。同时，RIIR通过将隐式正则化与显式损失梯度相融合，区别于以往的迭代式方法。 我们在多种医学图像数据集上开展的实验表明，RIIR具备更优的精度与数据效率。通过实验，我们还实证验证了其架构设计的有效性以及隐藏状态的价值——这两方面因素显著提升了配准精度与数据效率。研究结果显示，RIIR是一种高效且具有泛化能力的医学图像配准工具，并且有望扩展应用于其他高维优化问题。

Results

结果

4.1. Experiment 1: Comparison study with varying data availabilityAn illustrative visualization of RIIR inference on an example testdata, can be found in Fig. 5. The results for OASIS are presented inFig. 6, as well as . LapIRN, leveraging its multi-resolution architecture,also demonstrates robust performance. It is evident that RIIR outperforms most deep learning-based baselines when data availability isseverely limited and maintains consistent performance across variousdata availability scenarios, showcasing its data efficiency and accuracy.The results for NLST are shown in Fig. 7. An illustrative visualization of RIIR inference on an inhale-exhale lung CT pair, can be found inFig. 20. The registration of lung CT presents unique challenges due tothe large deformation between respiratory phases. RIIR demonstratessuperior performance in capturing these large deformations, achievinglower TRE while maintaining anatomically plausible transformations.The results of this experiment on mSASHA are shown in Fig. 8 usinga composition of boxplots. Both LapIRN and RCVM achieved superiorperformance in group-wise registration, with RCVM showing slightlybetter results in terms of PCA1. Our proposed RIIR demonstratedcomparable performance levels in terms of PCA1. The qualitativevisualization of RIIR inference on mSASHA test split is shown in Fig.21.For a comprehensive quantitative comparison, Table 1 presents detailed statistics across all datasets under full data availability, includingperformance metrics, model parameters, memory consumption, andcomputational time

4.1 实验1：不同数据可用性下的对比研究 在示例测试数据上对RIIR推理结果的可视化展示见图5。OASIS数据集的结果如图6及[此处原文省略的图表，通常为补充图表]所示。LapIRN算法凭借其多分辨率架构，同样展现出稳健的性能。显然，在数据可用性严重受限的情况下，RIIR的性能优于大多数基于深度学习的基准方法，且在不同数据可用性场景下均能保持稳定性能，这体现了其数据效率与准确性优势。 NLST数据集的结果如图7所示。在一对吸气-呼气肺部CT图像上对RIIR推理结果的可视化展示见图20。由于呼吸时相间存在较大形变，肺部CT配准面临独特挑战。RIIR在捕捉这些大幅形变方面表现出优越性能，不仅实现了更低的目标配准误差（TRE），同时还能保持符合解剖学合理性的变换。 本实验在mSASHA数据集上的结果通过箱线图组合形式展示于图8。LapIRN与RCVM两种方法在组级配准任务中均取得了较好性能，其中RCVM在DPCA1指标上的结果略优。我们提出的RIIR在DPCA1指标上展现出与上述两种方法相当的性能水平。在mSASHA测试集上对RIIR推理结果的定性可视化展示见图21。 为进行全面的定量对比，表1呈现了全数据可用情况下所有数据集的详细统计信息，包括性能指标、模型参数、内存消耗及计算时间。

Figure

图

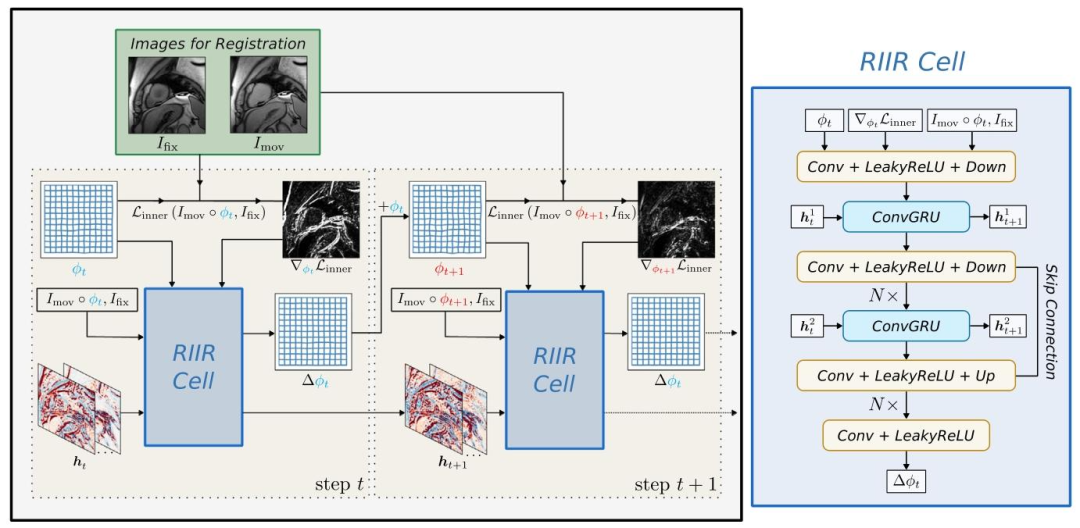
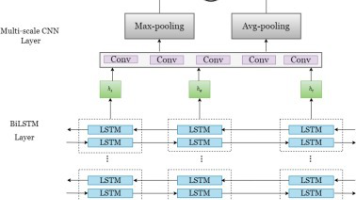
Fig. 1. Overview of RIIR framework. Here, an illustrative cardiac image pair is shown as an example. The hidden states 𝒉𝑡 = [𝒉 1 𝑡 , 𝒉 2 𝑡 ] are visualized in channel-wise fashion. Theinner loss inner is calculated during each step of RIIR thus dynamically changing. When 𝑡 = 0, the deformation field 𝝓0 is initialized as an identical transformation. In RIIR Cell,the dimensions of Conv and ConvGRU layer are dependent on the input (2D or 3D).

图1 RIIR框架概述 本图以心脏图像对为例进行说明。隐藏状态𝒉𝑡 = [𝒉₁𝑡 , 𝒉₂𝑡 ]采用按通道（channel-wise）的方式可视化呈现。内损失（inner）在RIIR的每一步推理过程中计算，因此其数值会动态变化。当𝑡 = 0时，形变场𝝓₀初始化为恒等变换（identical transformation，即初始状态下无位移的变换）。在RIIR单元（RIIR Cell）中，卷积层（Conv layer）与卷积门控循环单元层（ConvGRU layer）的维度由输入图像的维度（二维或三维）决定。

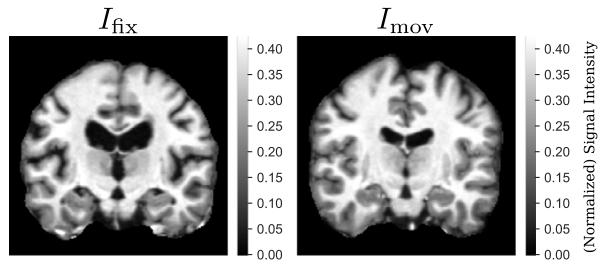
Fig. 2. An example of OASIS dataset for two subjects as 𝐼fix and 𝐼mov. The choices of𝐼*fix and 𝐼mov are random during training

图2 OASIS数据集示例 本图展示了OASIS数据集中两名受试者的图像，分别作为固定图像（𝐼fix）和浮动图像（𝐼mov）。在训练过程中，固定图像（𝐼fix）与浮动图像（𝐼mov）的选择是随机的。  

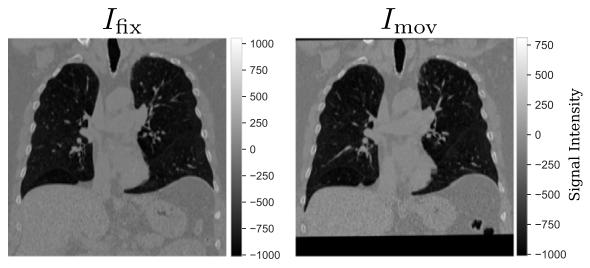
Fig. 3. An example of NLST dataset for a single subject with 𝐼fix corresponding to theimage captured at inspiratory phase and 𝐼mov corresponding to the image captured atexpiratory phase

图3 NLST数据集示例 本图展示了NLST数据集中一名受试者的图像，其中固定图像（𝐼fix）对应吸气相采集的图像，浮动图像（𝐼mov）对应呼气相采集的图像。

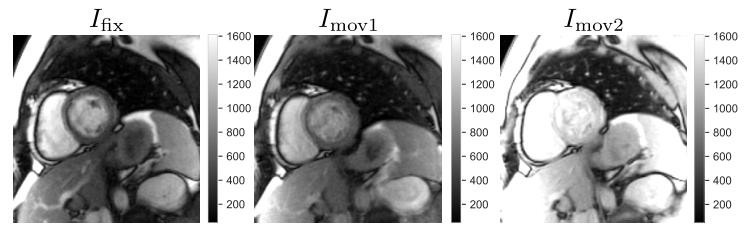
Fig. 4. An example of mSASHA dataset, from left to right: 𝐼fix, 𝐼mov (random sample1), and 𝐼mov (random sample 2). The three images were taken from the same imageseries, with different acquisition time points. To emphasize the difference in both signalintensity and contrast across images in a single series, the color ranges are set to bethe same for the three images.

图4 mSASHA数据集示例 从左至右依次为：固定图像（𝐼fix）、浮动图像1（𝐼mov，随机样本1）、浮动图像2（𝐼mov，随机样本2）。这三幅图像来源于同一图像序列，采集时间点各不相同。为突出同一系列图像间在信号强度与对比度上的差异，三幅图像的颜色范围（color range）设置保持一致。  

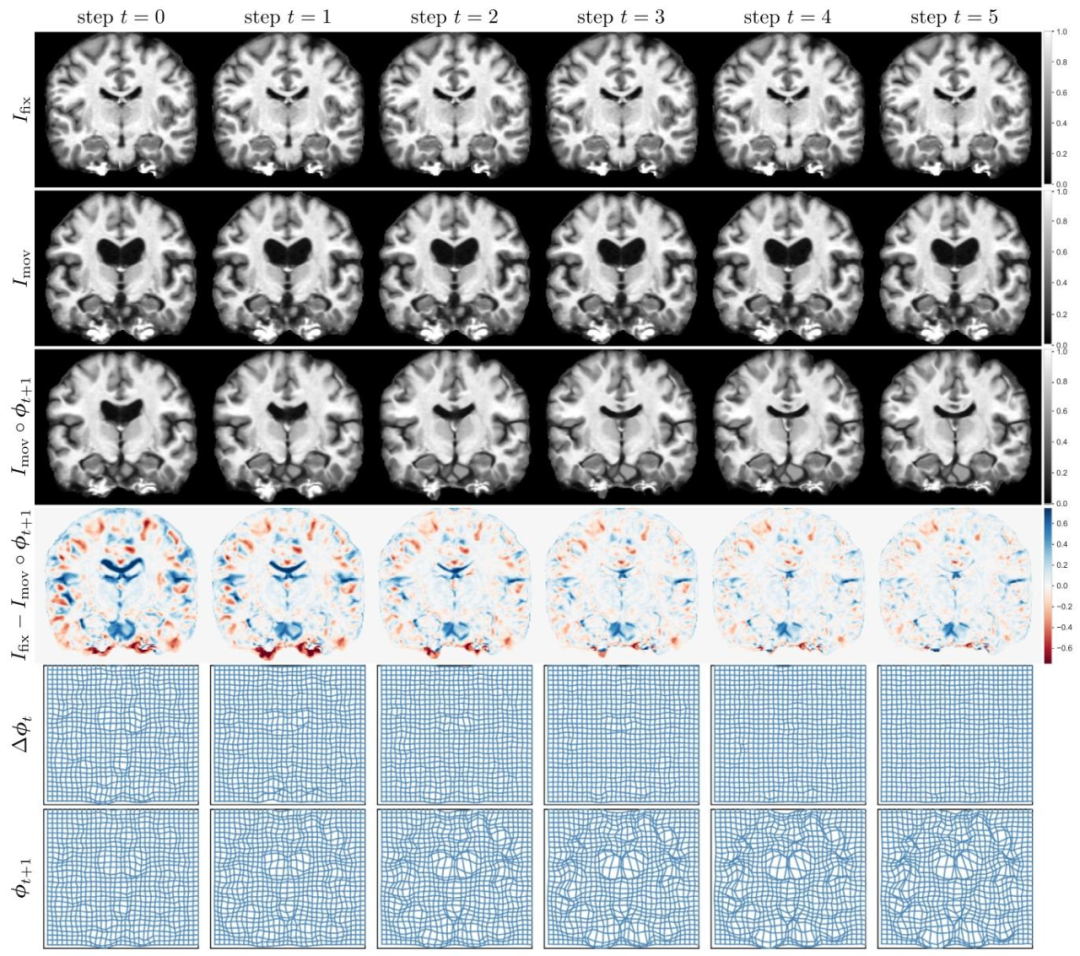
Fig. 5. A visualization of RIIR inference on OASIS test split, visualized with a 2D slice and in-plane deformation. The inference step was set to 6 in both training and inference.All images in the same row were plotted using the same color range for better consistency

图5 OASIS测试集上RIIR推理结果可视化 本图采用二维切片（2D slice）与面内形变（in-plane deformation）的形式，展示了RIIR在OASIS测试集上的推理结果。训练与推理过程中，推理步数（inference step）均设为6。  

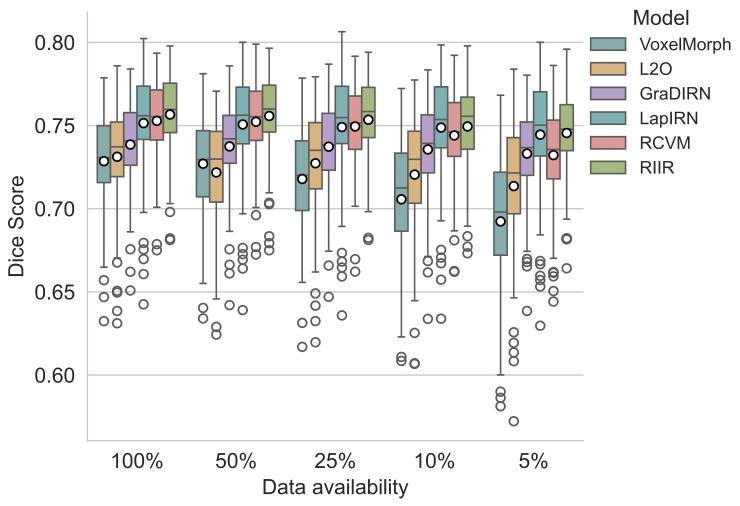
Fig. 6. Results of Experiment 1 with boxplots for Dice score on OASIS. The circledenotes the mean of the metric of interest. The segmentation metric Dice is calculatedfor all 35 segmentation labels and post-processed by taking the average.

图6 实验1结果：OASIS数据集上Dice系数的箱线图 本图为实验1的结果展示，通过箱线图呈现了OASIS数据集上的Dice系数（Dice score）分布情况。图中的圆圈代表所关注指标（即Dice系数）的均值。  能稳定性与平均水平。

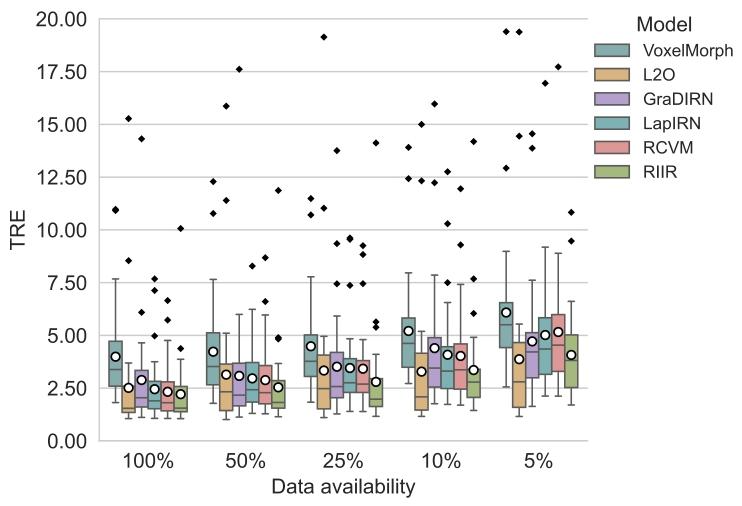
Fig. 7. Results of Experiment 1 with boxplots for TRE on NLST. The circle denotesthe mean of the metric of interest. The TRE is calculated based on the anatomicallymeaningful keypoint pairs provided by corrField algorithm within lung lobes. Forvisualization, outliers over a TRE of 20 mm were excluded but used for statisticalcalculation.

 图7 实验1结果：NLST数据集上TRE的箱线图 图中的圆圈代表所关注指标（TRE）的均值。TRE（目标配准误差）基于corrField算法在肺叶内提供的具有解剖学意义的关键点对计算得出。为便于可视化，TRE超过20毫米的异常值已被排除，但这些异常值仍用于统计计算。

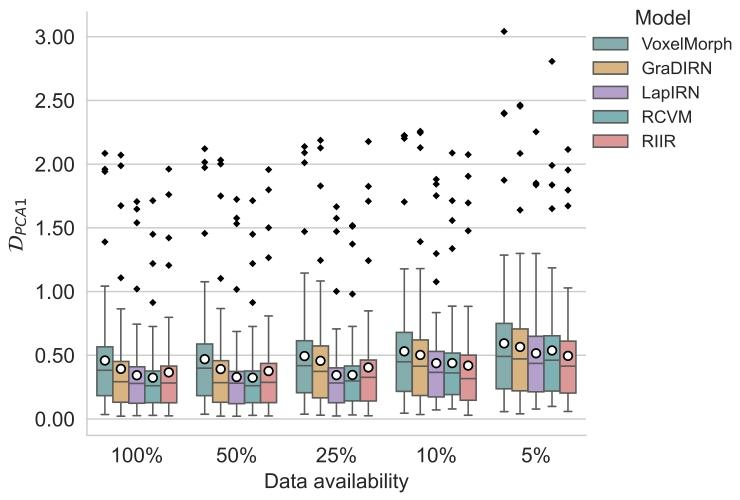
Fig. 8. Results of Experiment 1 with boxplots for 𝐷𝑝𝑐𝑎1 on mSASHA. The circle denotesthe mean of the metric of interest. The group-wise metric 𝐷PCA1 was calculated basedon further center-cropping at a ratio of 70% on the warped images

图8 实验1结果：mSASHA数据集上𝐷ₚ𝒸𝒶¹的箱线图 本图为实验1的结果展示，通过箱线图呈现了mSASHA数据集上𝐷ₚ𝒸𝒶¹（DPCA1）指标的分布情况。

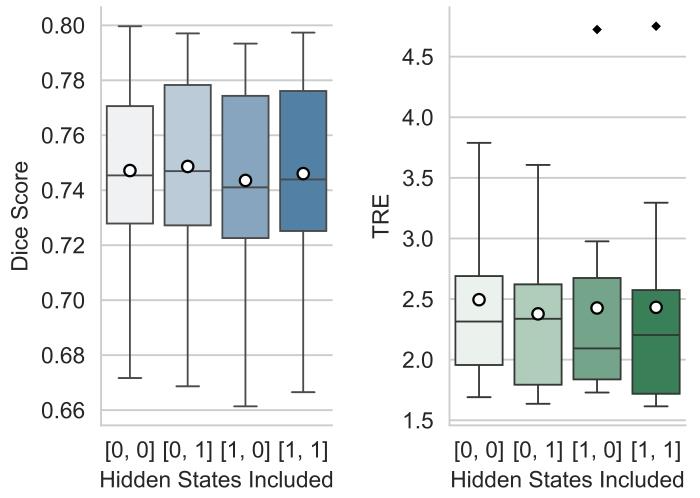
Fig. 9. Results of Experiment 2 evaluated on OASIS validation set (left) regarding Dicescore and NLST validation set (right) regarding TRE. Here, for example, [0, 0] denotesthe case that no hidden states are considered, and [1, 1] denotes both hidden stateswere considered in the pipeline. Two-sided Wilcoxon tests were conducted for [0, 1]against other settings with statistical significance (p< 0.05), except for [0, 0] (𝑝 = 0.076)in OASIS dataset.

图9 实验2结果：基于OASIS验证集（左侧，Dice系数）与NLST验证集（右侧，TRE）的评估 例如，[0, 0]表示未考虑任何隐藏状态的情况，[1, 1]表示在流程中同时考虑了两种隐藏状态的情况。针对[0, 1]设置与其他设置，进行了双侧Wilcoxon检验，结果显示除OASIS数据集上[0, 0]设置（p=0.076）外，其余对比均具有统计学显著性（p<0.05）。

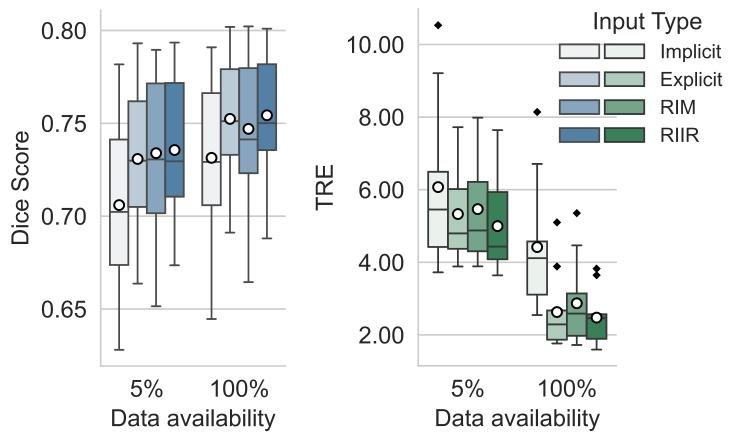
Fig. 10. Results of Experiment 3 evaluated on OASIS validation set (left) andNLST validation set (right). For OASIS with 5% data availability, RIIR input showssignificance over all types except RIM (𝑝 = 0.81). At 100%, significance remains exceptfor Explicit input (𝑝 = 0.17). For NLST with 5% data availability, RIIR input showssignificance over all types. At 100%, significance remains except for Explicit input(𝑝 = 0.27)

图10 实验3结果：基于OASIS验证集（左侧）与NLST验证集（右侧）的评估 在OASIS数据集5%数据可用的情况下，RIIR输入（方案）相较于其他所有输入类型均表现出统计学显著性，仅与RIM输入（方案）对比时无显著性差异（p=0.81）；在100%数据可用的情况下，除与“显式输入（Explicit input）”对比时无显著性差异（p=0.17）外，RIIR输入（方案）相较于其他输入类型仍保持统计学显著性。 在NLST数据集5%数据可用的情况下，RIIR输入（方案）相较于所有其他输入类型均表现出统计学显著性；在100%数据可用的情况下，除与“显式输入（Explicit input）”对比时无显著性差异（p=0.27）外，RIIR输入（方案）相较于其他输入类型仍保持统计学显著性。

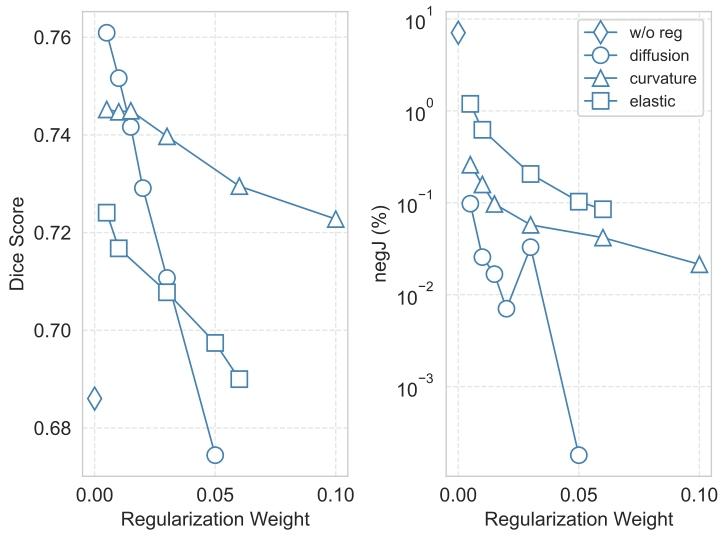
Fig. 11. Results of regularization analysis on OASIS validation set. Different regularization weights are compared in terms of Dice score. Here w/o reg denotes theresults without regularization and negJ denotes the percentage of negative Jacobiandeterminant

图11 OASIS验证集上的正则化分析结果 本图基于Dice系数，对比了不同正则化权重的性能表现。其中，“w/o reg”表示无正则化（即未施加正则化约束）的结果，“negJ”表示雅可比行列式为负（negative Jacobian determinant）的比例（用于评估配准变换的拓扑合理性，负雅可比行列式比例越低，说明变换越符合解剖结构的物理连续性）。

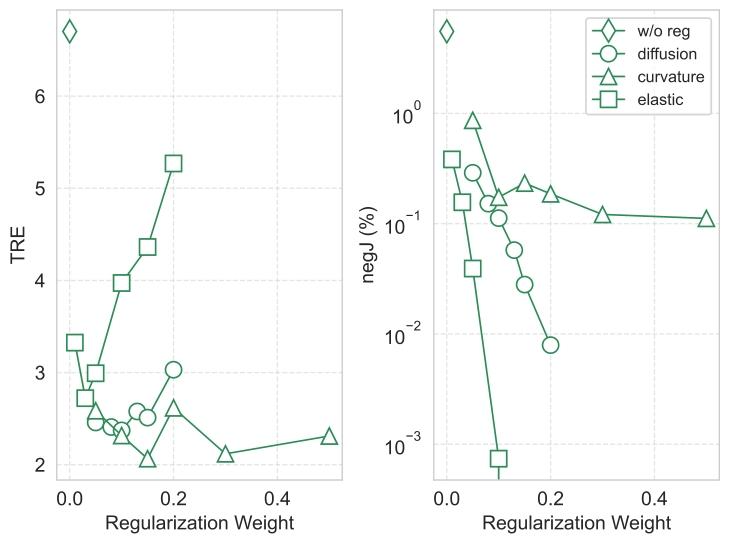
Fig. 12. Results of regularization analysis on NLST validation set. Different regularization weights are compared in terms of TRE. Here w/o reg denotes the results withoutregularization and negJ denotes the percentage of negative Jacobian determinant.

图12 NLST验证集上的正则化分析结果 本图基于目标配准误差（TRE），对比了不同正则化权重的性能表现。其中，“w/o reg”表示无正则化（即未施加正则化约束）的结果，“negJ”表示雅可比行列式为负（negative Jacobian determinant）的比例。

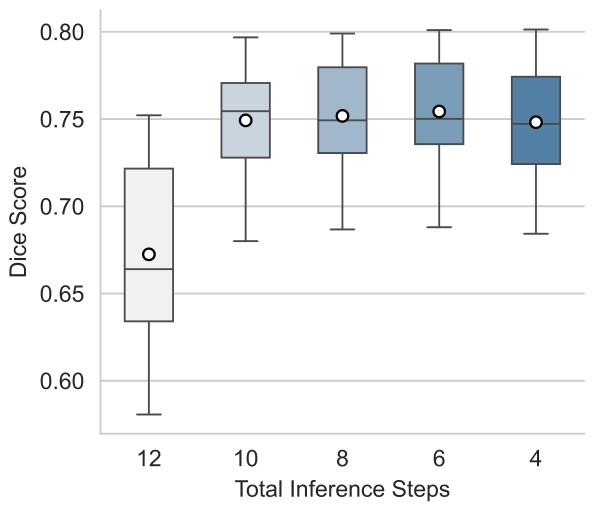
Fig. 13. Results of Experiment 5. For the ablation study on network steps on OASIS,two-sided Wilcoxon tests suggest significant difference is found for 𝑡 = 6 against allother scenarios.

图13 实验5结果 本图为OASIS数据集上针对网络步数（network steps）的消融实验结果。双侧Wilcoxon检验表明，当网络步数𝑡 = 6时，其结果与其他所有步数场景的结果相比，均存在统计学显著差异。

Table

表

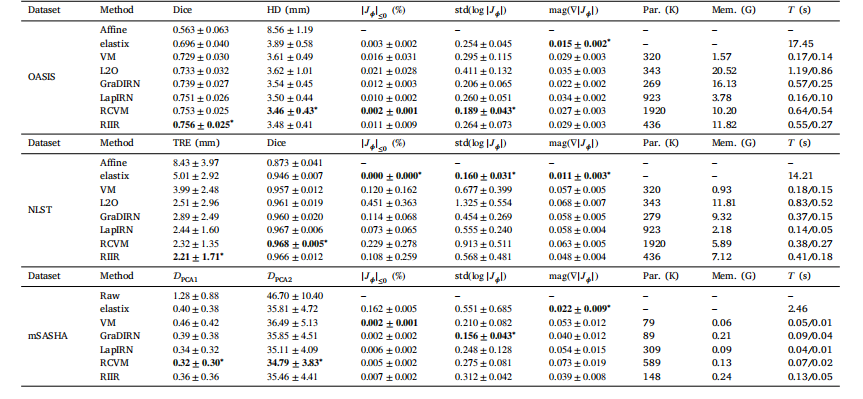
Table 1Quantitative comparison of different registration methods with 100% data availability. For each evaluation metric except Par. (number of parameters), Mem. (VRAM consumption),and 𝑇 (training/inference time), we report mean ± std. VRAM consumption indicates the peak GPU memory consumption during training. The training/inference time is profiledfor a batch on GPU (excluding data loading time), except for elastix where CPU time is reported. For LapIRN, metrics are reported at level 3. The best performance is shown inbold and marked with ∗ if there is a statistically significant difference (𝑝 < 0.05) from the second best by a two-sided Wilcoxon signed-rank test

表1 100%数据可用情况下不同配准方法的定量对比 除参数数量（Par.）、内存消耗（Mem.，即显存消耗）和时间（𝑇，训练/推理时间）外，其余各评估指标均以“均值±标准差”（mean ± std.）形式呈现。其中，显存消耗指训练过程中GPU的峰值内存占用；训练/推理时间为在GPU上处理一个批次数据的耗时（不含数据加载时间），而elastix方法的时间为CPU处理耗时。对于LapIRN方法，其各项指标均基于第3层级（level 3）的数据计算得出。 性能最优的结果以粗体标注；若通过双侧Wilcoxon符号秩检验（two-sided Wilcoxon signed-rank test）验证，该最优结果与次优结果存在统计学显著差异（𝑝<0.05），则额外标注“∗”。

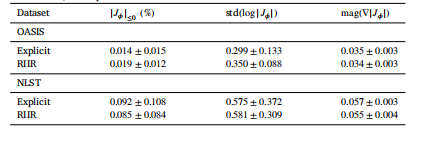
Table 2Comparison of Explicit Input and RIIR under 5% data availability in Experiment 3. Foreach metric, we report mean ± std

表2 实验3中5%数据可用情况下“显式输入（Explicit Input）”与RIIR的对比 对于各项指标，均以“均值±标准差”（mean ± std）的形式呈现结果。