Distill文章-A gentle introduction to graph Neural Networks(图神经网络是怎么构造的)
详解图神经网络
目录
1 简介
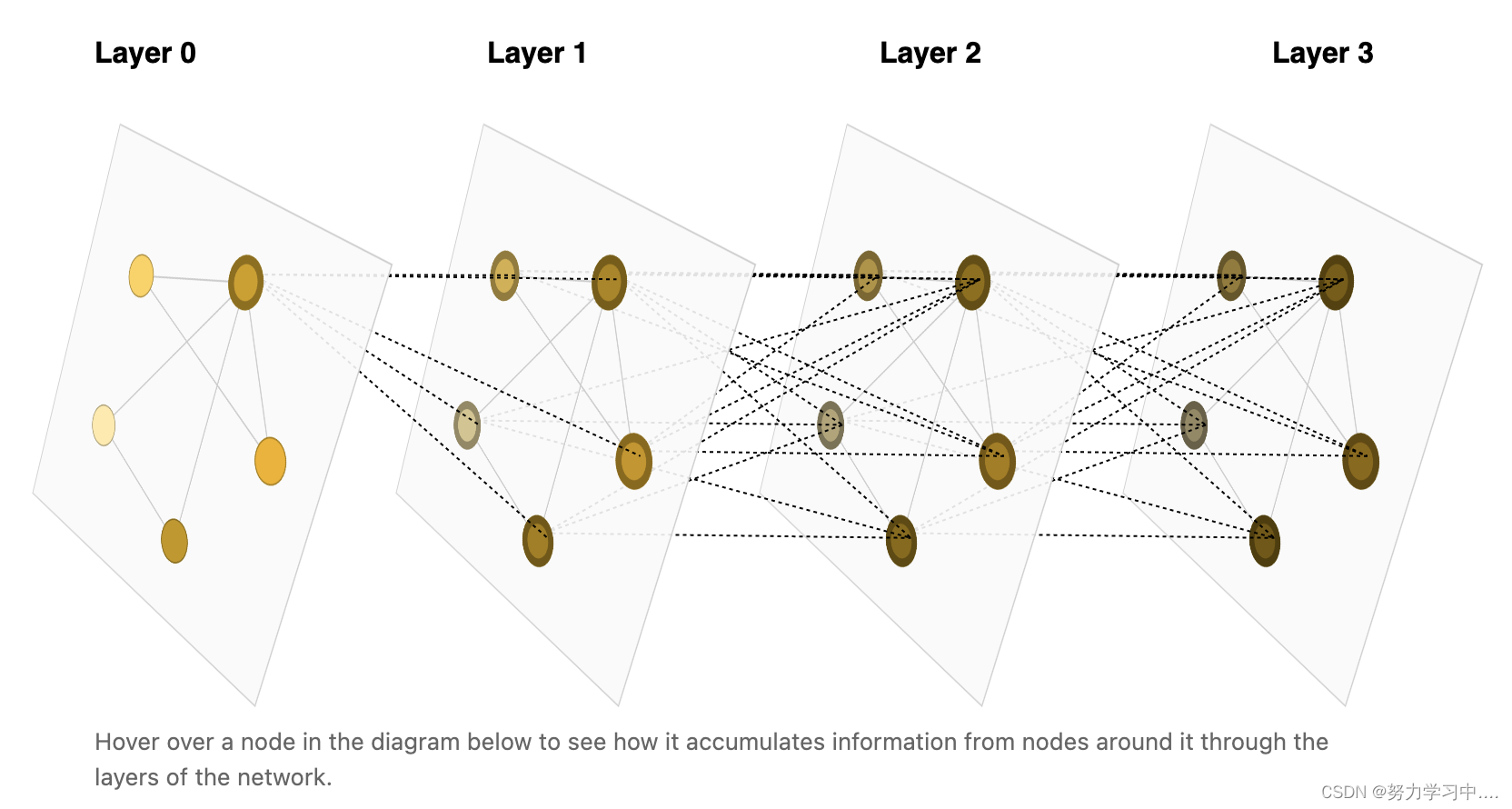
1. 当图层数越深时,节点的值是由其邻居的邻居的邻居计算而来;只要足够深,一个节点是能够处理一个图里面大范围的节点信息---也就是图神经网络怎么利用图结构化来处理信息的;
2. distill介绍:
Google Brain的Chris Olah和Shan Carter发布了一份专注于机器学习研究的新期刊:Distill;
不同于过去百余年间的论文,Distill将利用互联网,以可视化、可交互的形式来展示机器学习研究成果。
distill网站上发表的文章都有什么特点:其写作是很自由的,通常可以从头读到尾;
distill上的文章大部分是用图来解释(文字基本都是对图的解释)
用户可以在网站上改变模型的结构,尝试不同的假设条件,并且可以立刻看到操作对结果的影响;
这能帮助用户们快速建立对文章的理解。
3. 十几年前提出了图神经网络(GNN),如今在能力上,表达力上都有了提高;
也开始应用,但目前能看到的应用不那么多;
4. 这片文章主要介绍了:
探索和解释现代图神经网络;
什么数据可以表示一张图;
图神经网络到底有什么不一样的地方;
构建一个GNN看看各个模块长什么样;
搭建 GNN playground--作者花了很大的心思;
2 图的介绍
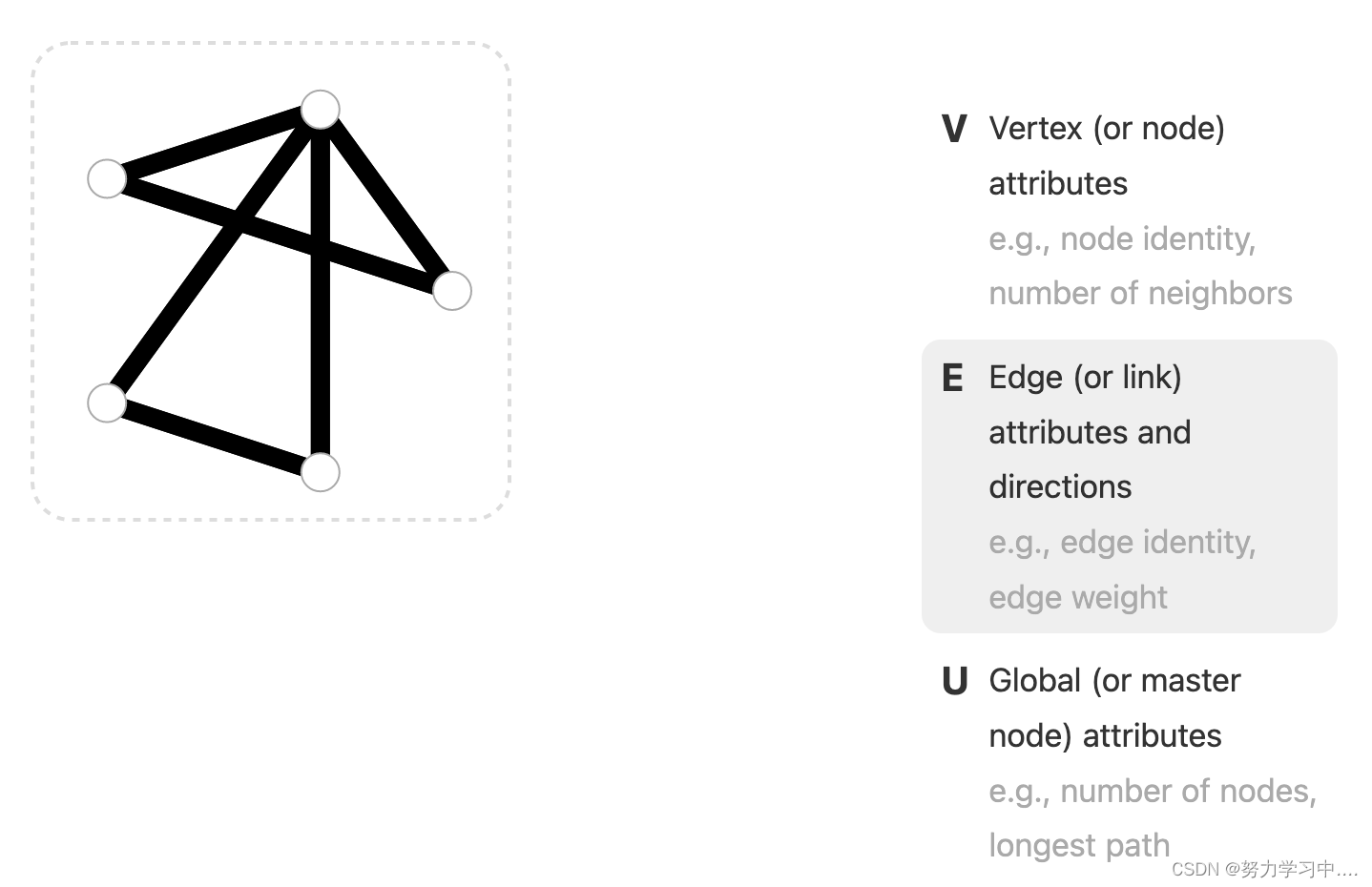
1. 图,用一个长度向量表示节点;另一个长度向量表示边;全局信息用另外一个向量表示;
3 数据如何表示成图
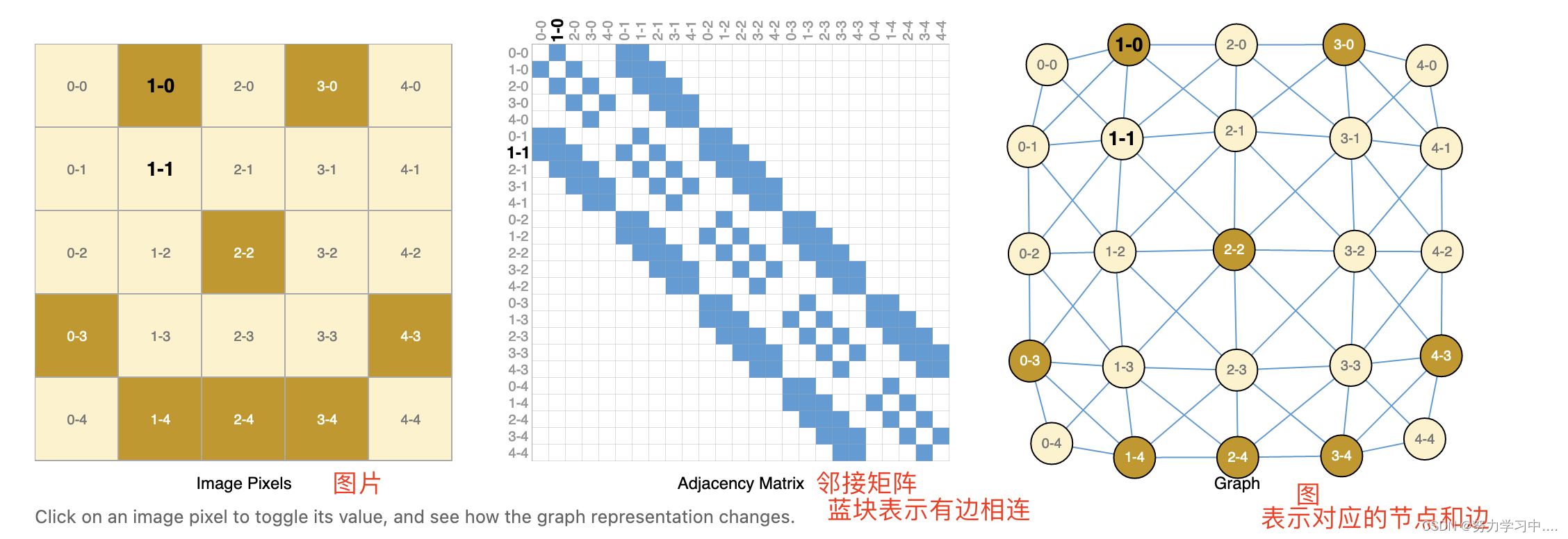
1. 图片表示为图:
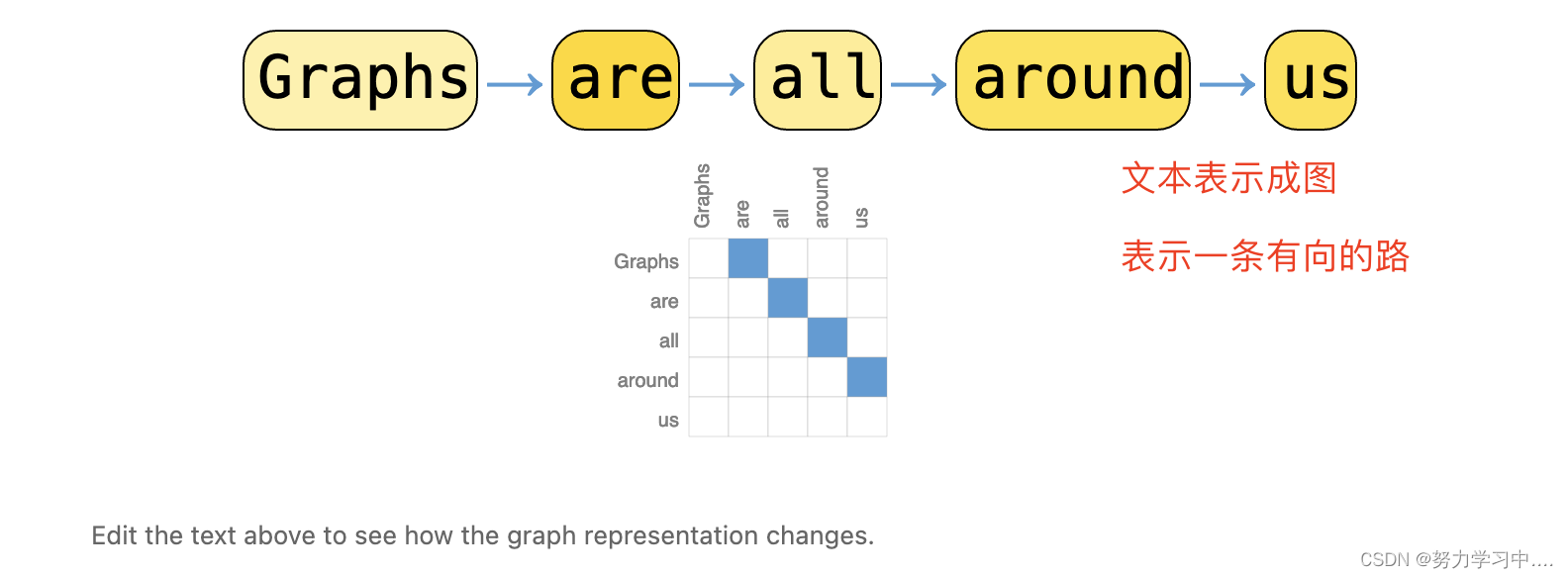
2. 文字表示为图:
3. 现实生活中,还有很多东西可以表示为图(如分子表示为图):

4. 社交网络图:
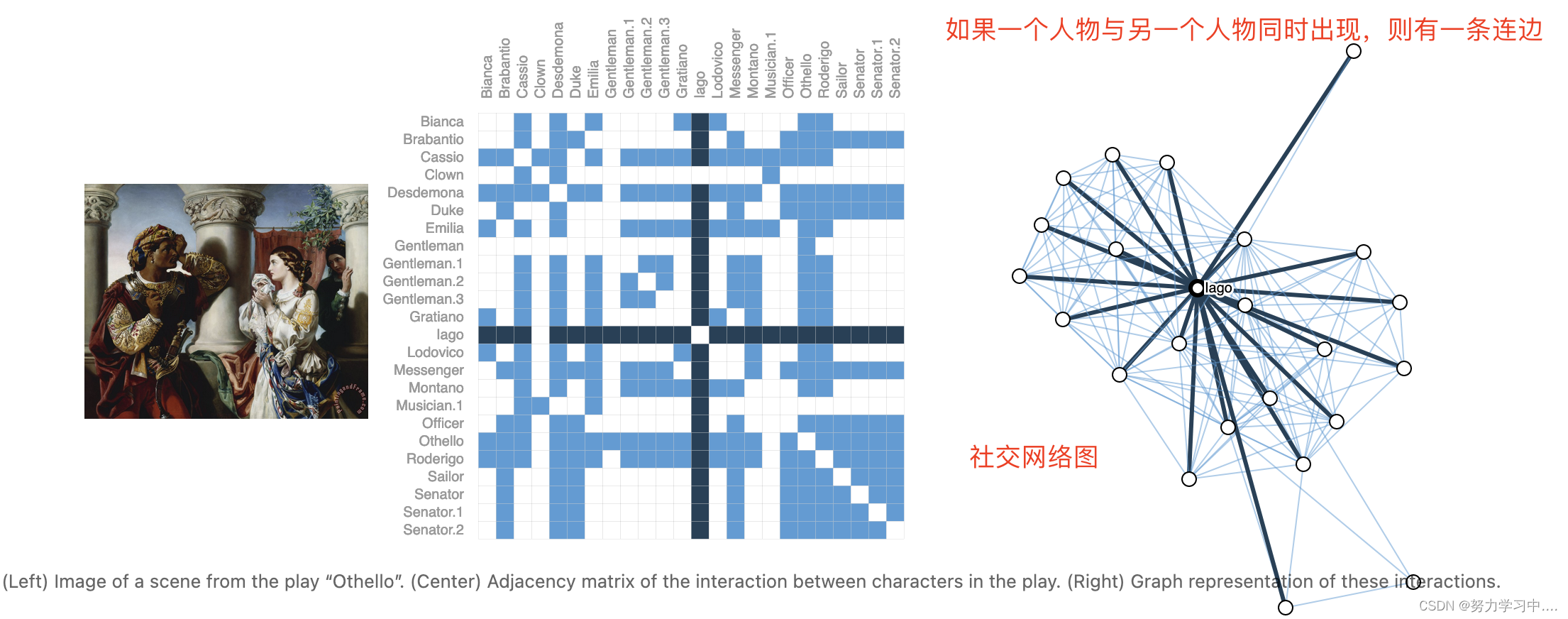
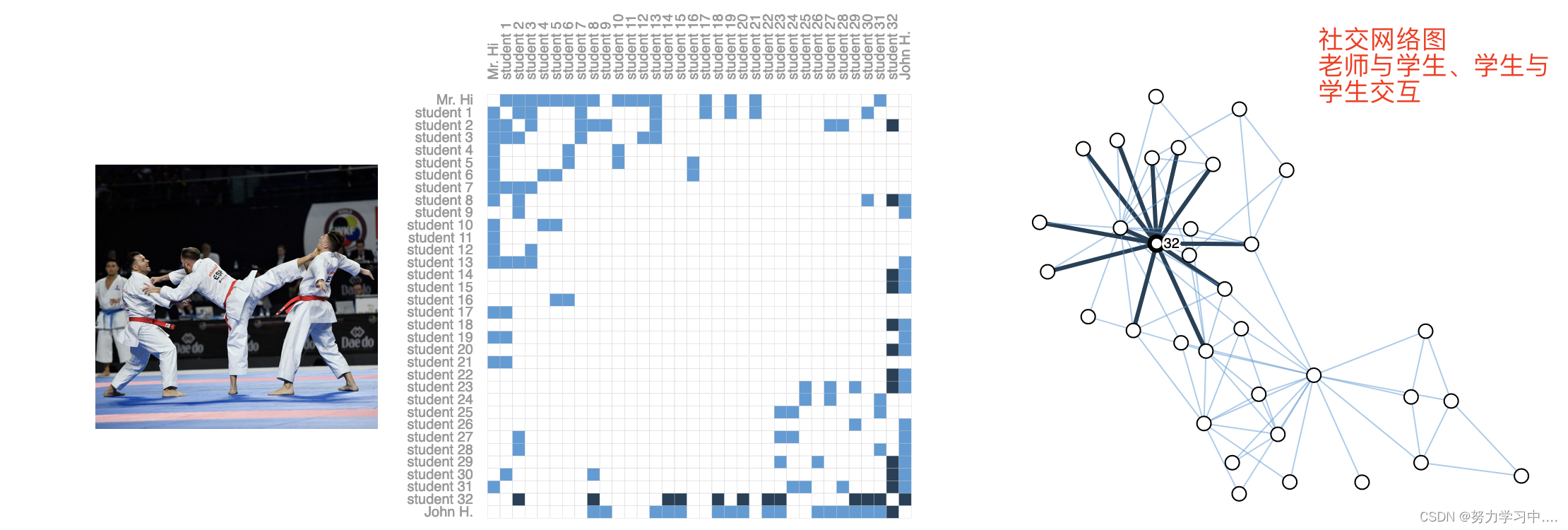
5. 引用图(有向边) :一篇论文是否引用另一篇论文
6. 其他例子:
在计算机视觉中,我们有时想要标记视觉场景中的对象。然后,我们可以通过将这些对象视为节点并将它们的关系视为边来构建图形;
机器学习模型、编程代码和数学方程也可以表述为图,其中变量是节点,边是以这些变量作为输入和输出的操作;
7. 图与节点、边的统计
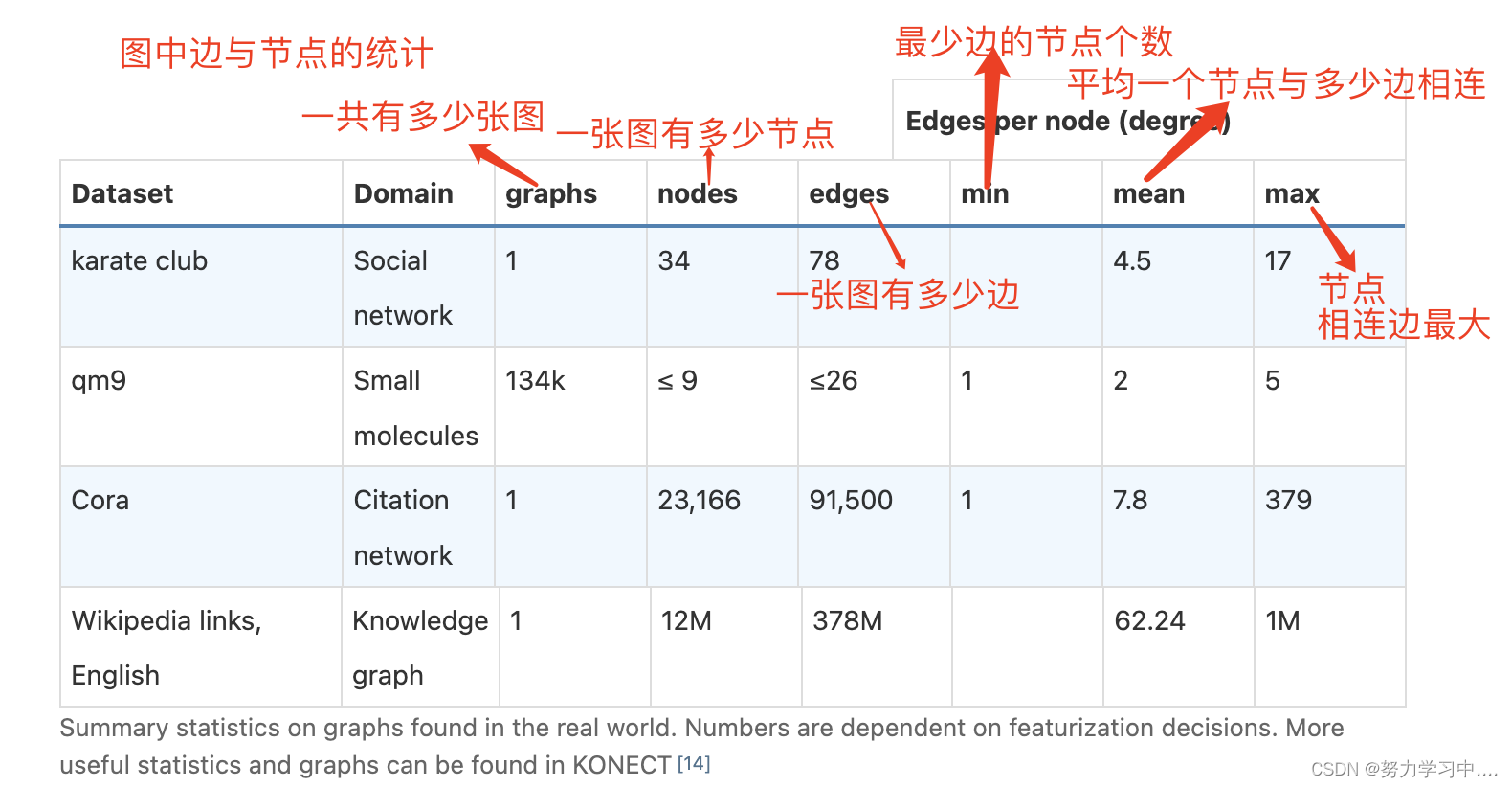
4 三大类问题
1. 图层面、边层面、节点层面
2. 图层面:比如图分类
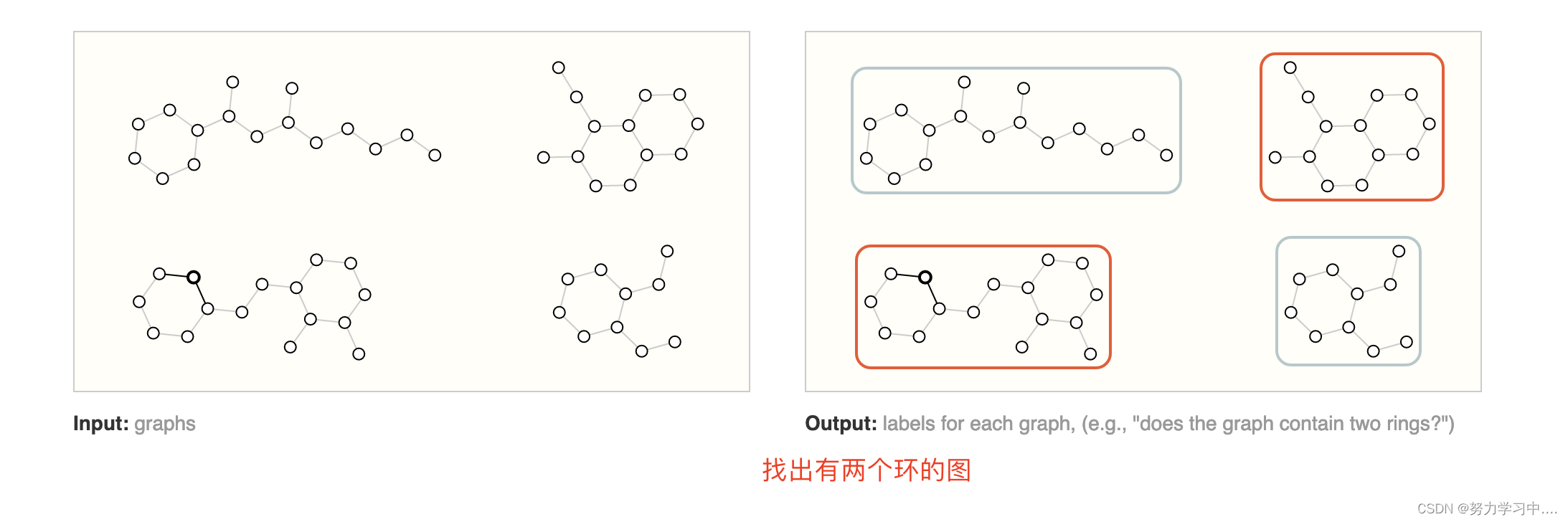
3. 节点层面:

4. 边层面:
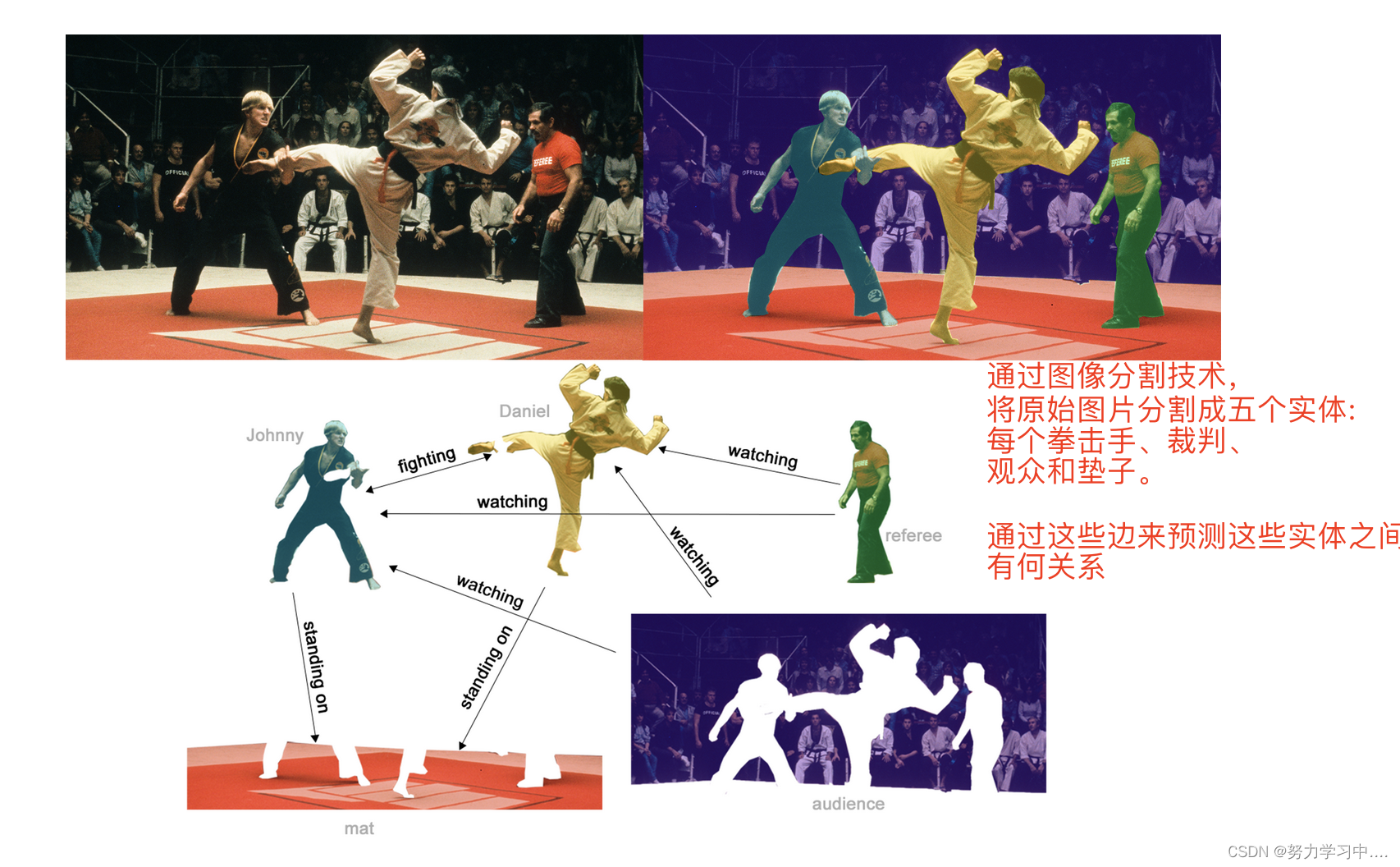
5. 给一个图,把边上的每个属性预测出来:
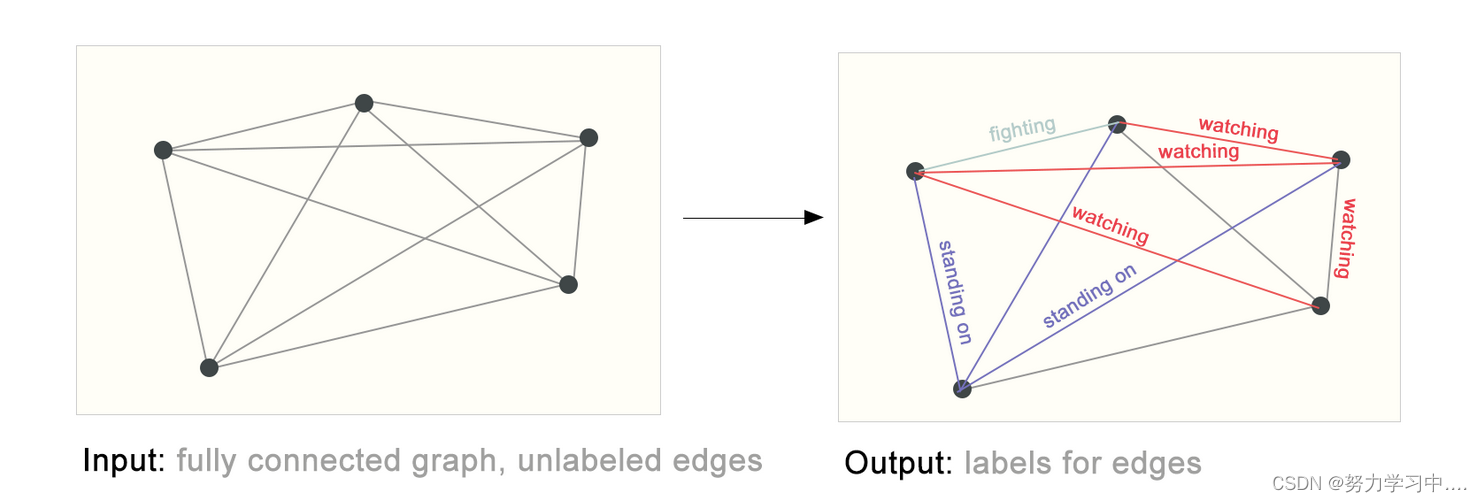
5 将机器学习(神经网络)用在图上,会遇到什么挑战
1. 怎样表示图,使其与神经网络兼容
2. 图上有四种信息:节点、边、全局上下文和(前面三个都可以用向量表示)连接性
3. 连接性如何表示?
邻接矩阵?方形矩阵,有很多问题;
如矩阵较大,比如Wikipedia的图,有12W+的点,那么这个矩阵就有12000000*12000000个点,可能使用稀疏矩阵来存;
但是关于稀疏矩阵的计算又比较难;
邻接矩阵把任何行或者列交换,都不会影响这个邻接矩阵:
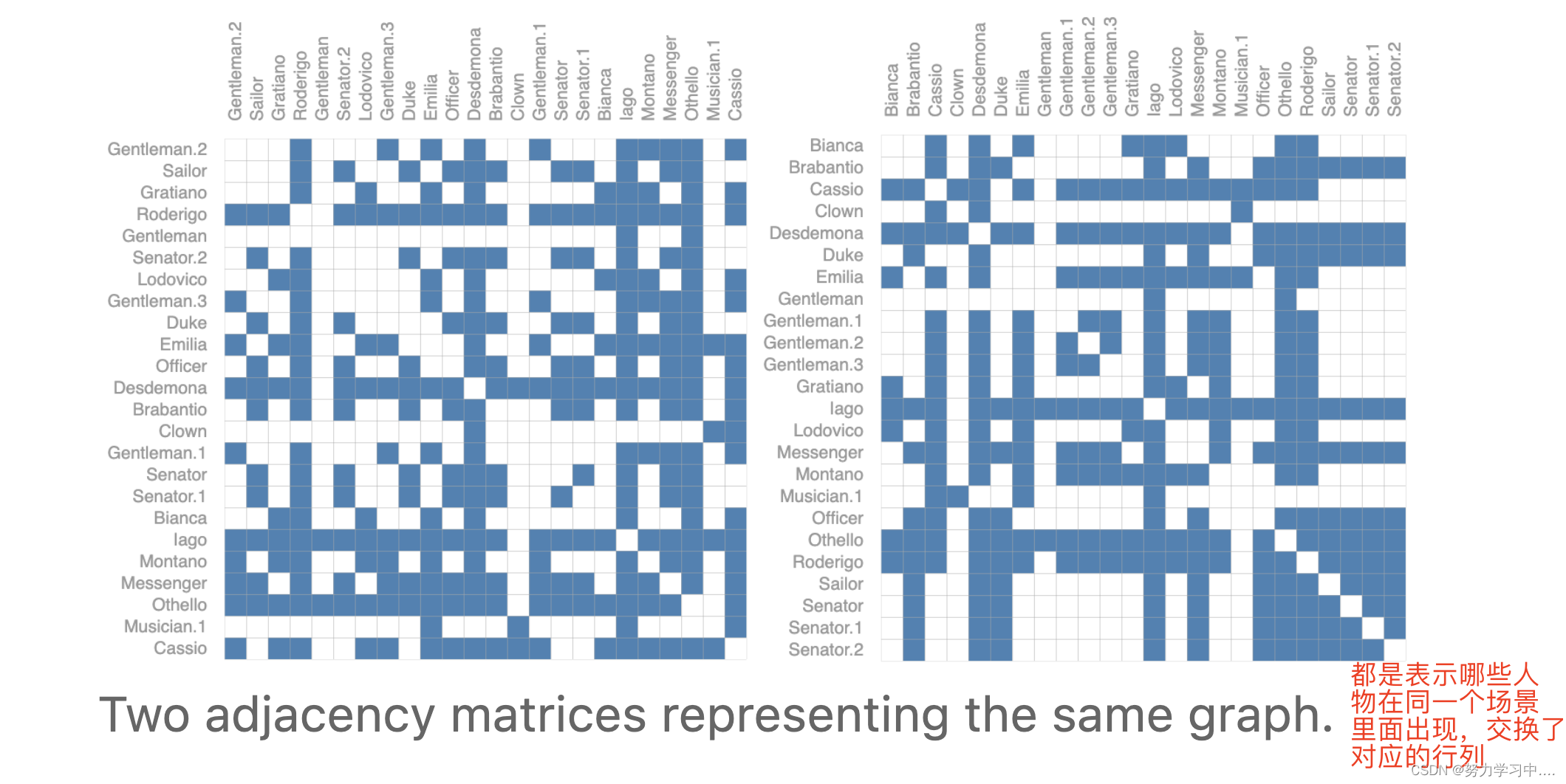
视觉上不一样, 但是神经网络要求,这两种邻接矩阵,不论你将哪个放入神经网络中,你都要保证最后的结果一样;
因为他们代表的是同一张图;
形象化的例子:
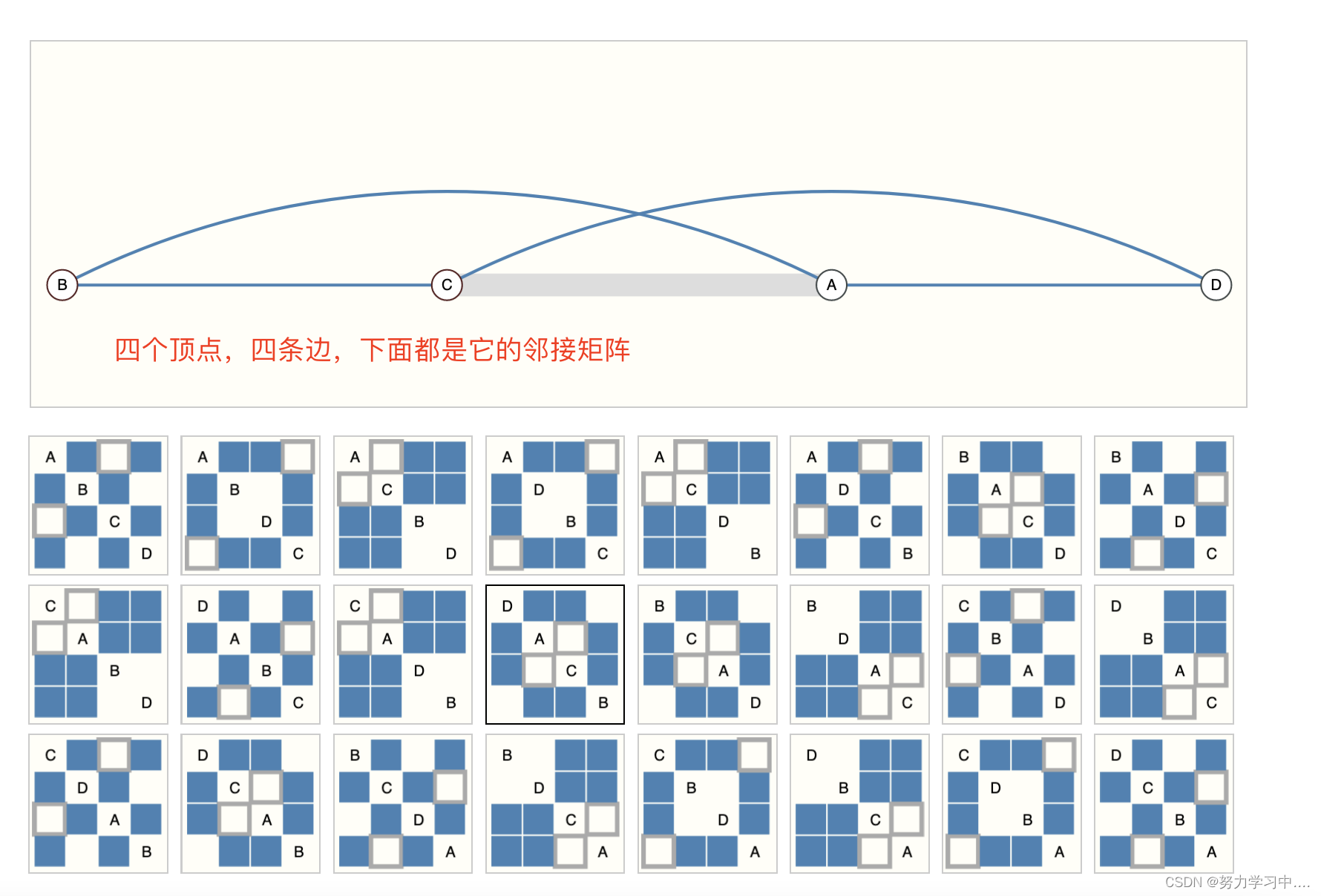
4. 如果又想存储高效,又想排序不会影响最后结果,该如何存(下图就是方法):
当打乱边的顺序,对应的邻接列表的顺序也打乱;
顶点打乱,只需要将邻接列表中的数字做相应更新;
既是存储高效的,也是和列无关的;
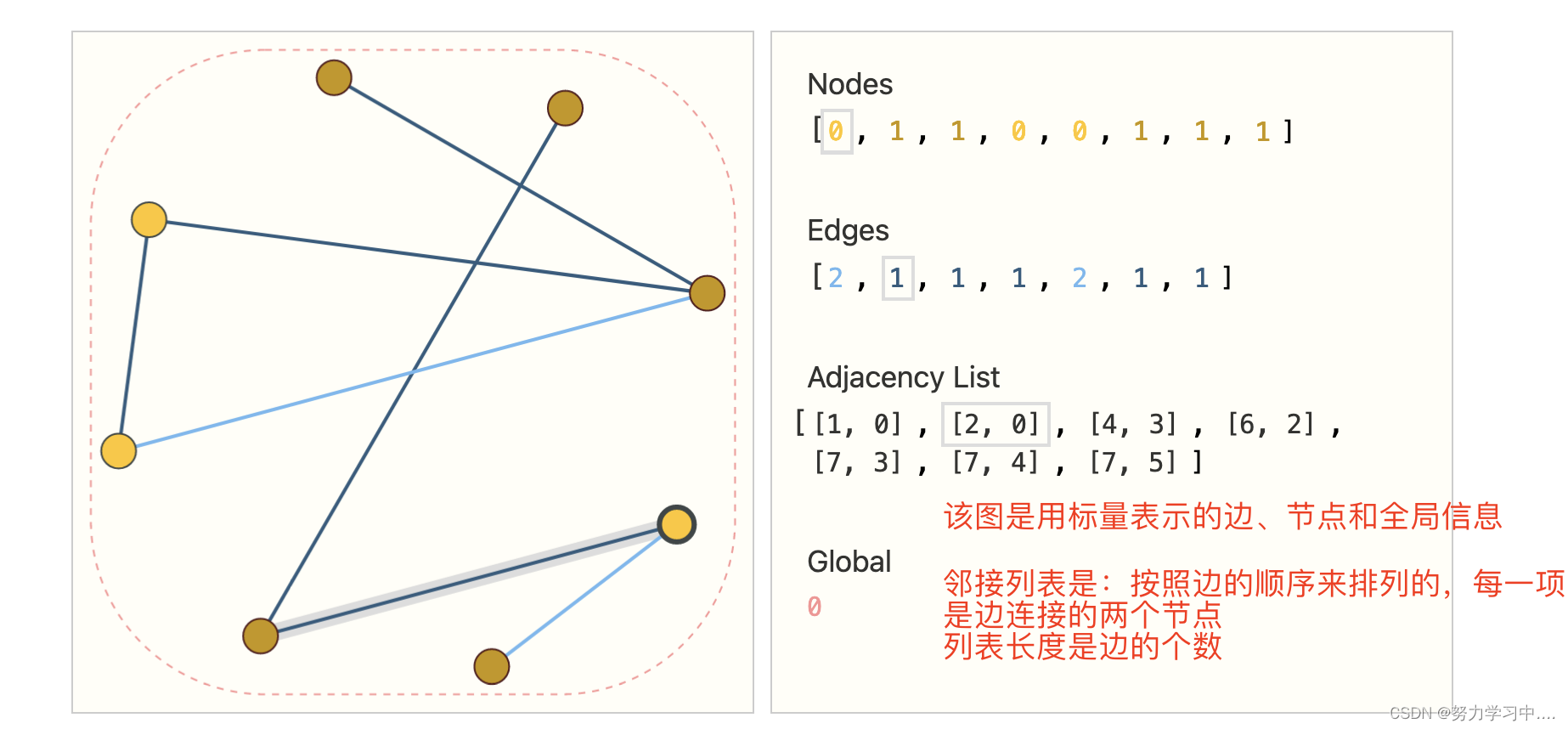
5. 给神经网络这样的一个数据形式,怎么样用神经网络来处理
图神经网络(GNN):对图上所有属性(顶点、边、全局上下文)进行可以优化的变换,这个变换可以保持图的对称信息(顶点进行另外一种排序后,结果不会改变)
信息传递的网络,输入是一个图,输出也是一个图;
会对属性进行变换,不会改变图的连接性;
6 最简单的GNN
1. 用3个MLP(多层感知机),是对三种向量独自作用,所以不管对顶点做如何排序,都不会改变结果;
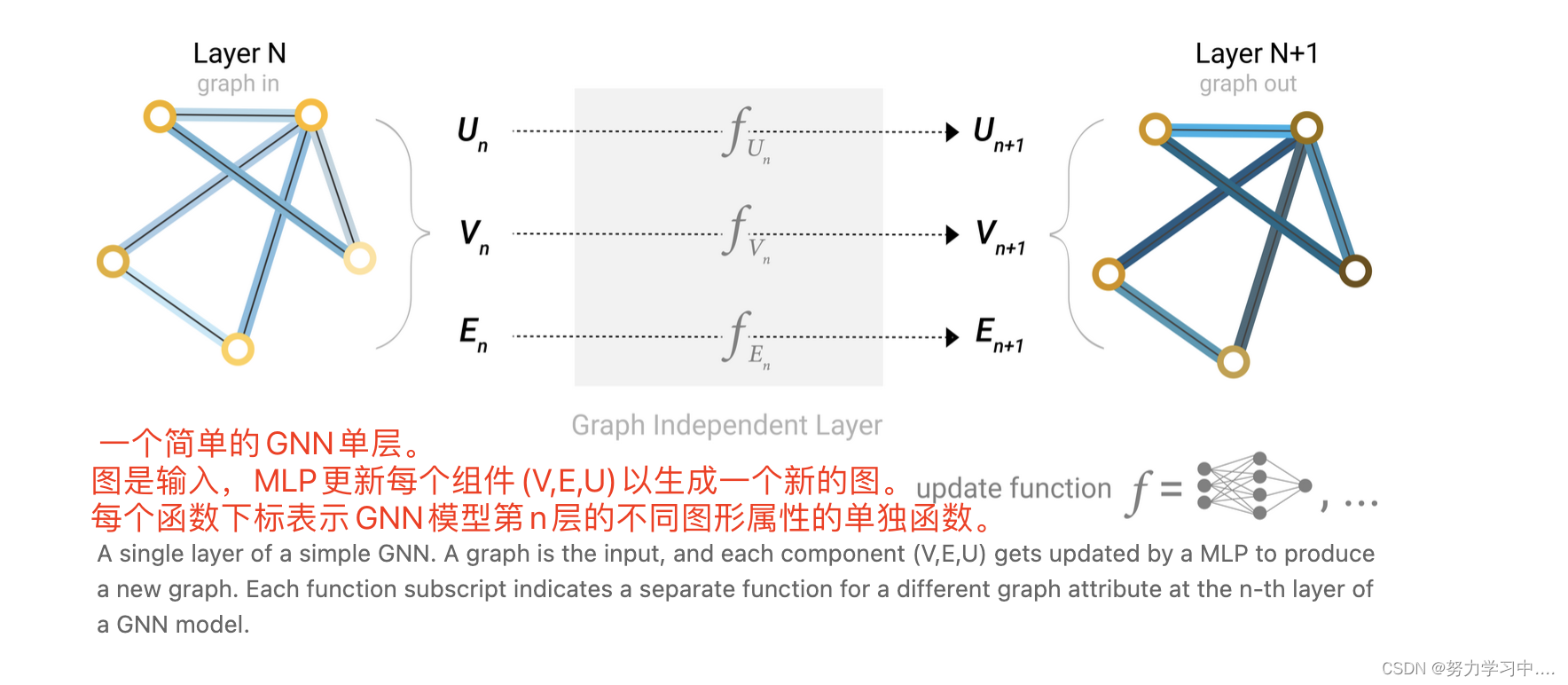
2. 最后一层的输出,如何得到要的预测值
比如每个节点都有一个向量表示,如果做分类问题(比如,前面那个学生选择哪个老师,就是做一个输出维度为2的一个全连接层,得到输出)做回归,输出一个值;
这里所有的顶点共享一个全连接层里面的参数。
3. 还想对顶点做预测,但是这个节点不知道其向量表示,我该如何表示这个节点的向量呢?
可以把与这个节点相连的边的向量拿出来,把全局的向量拿出来
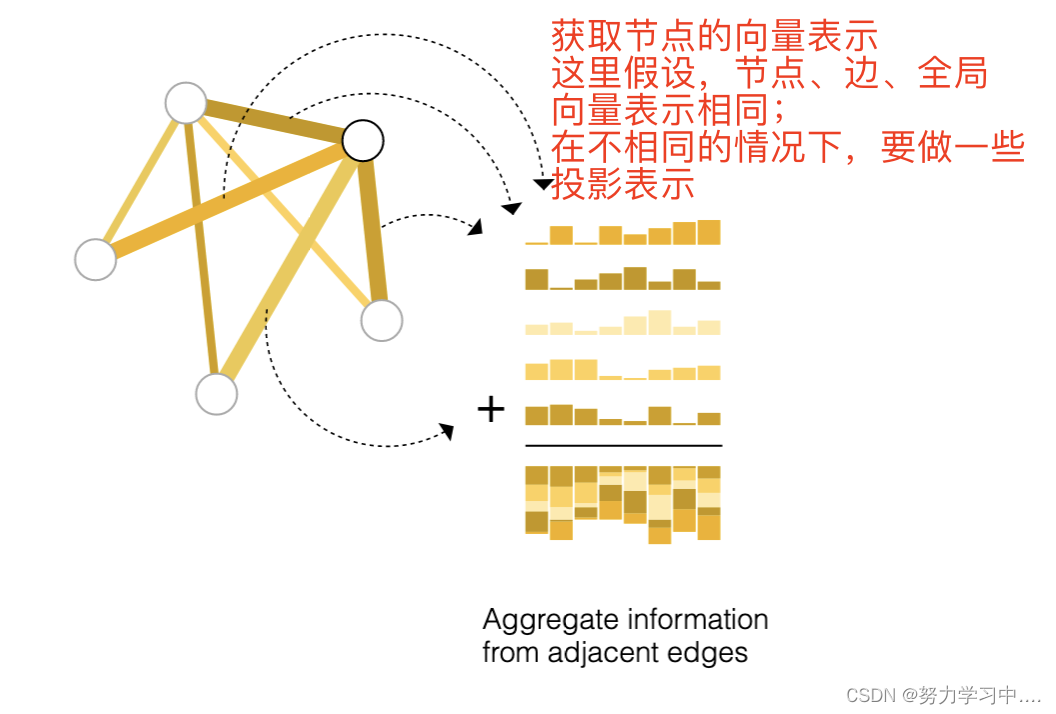
形象化的表示 :
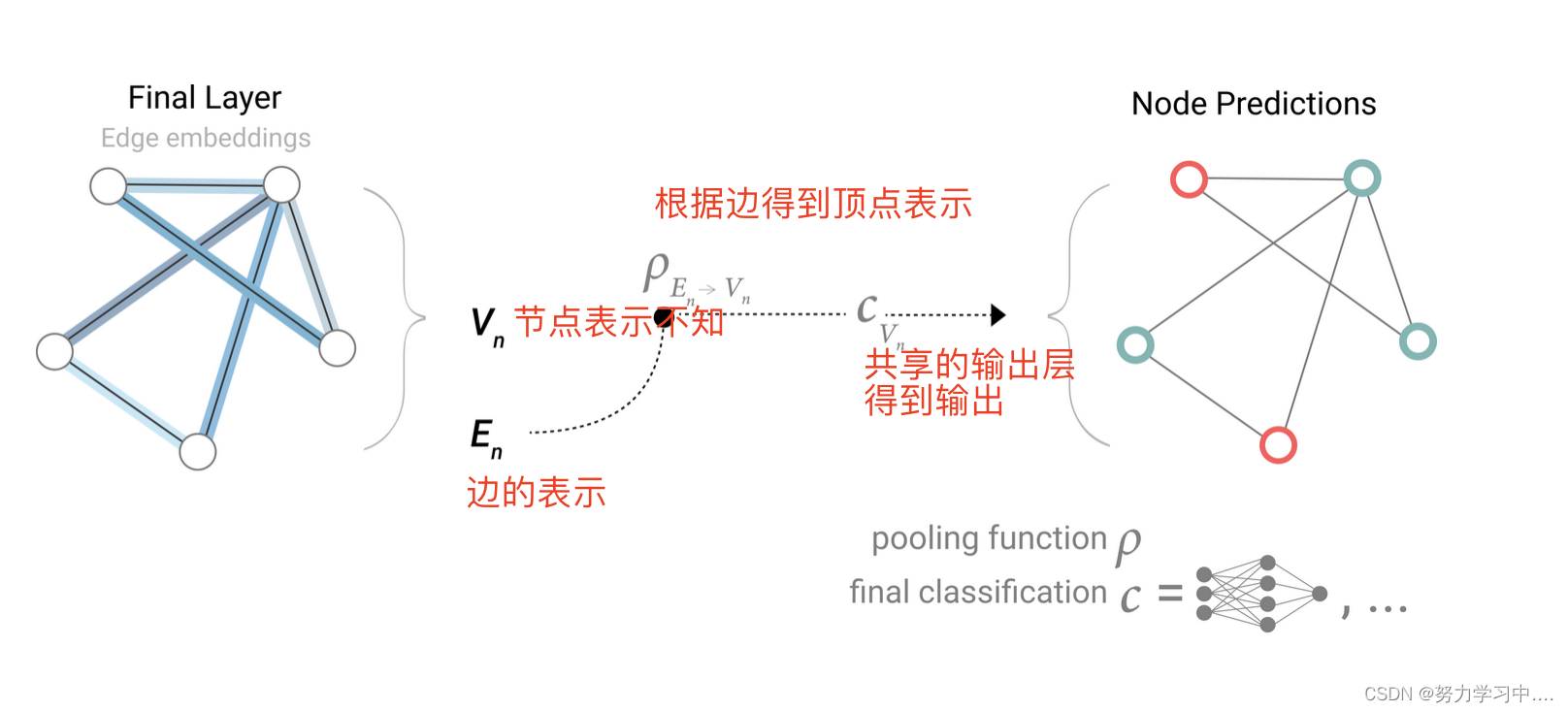
4. 同样道理,如果不知道边的向量表示,可以将顶点的向量汇聚到边上
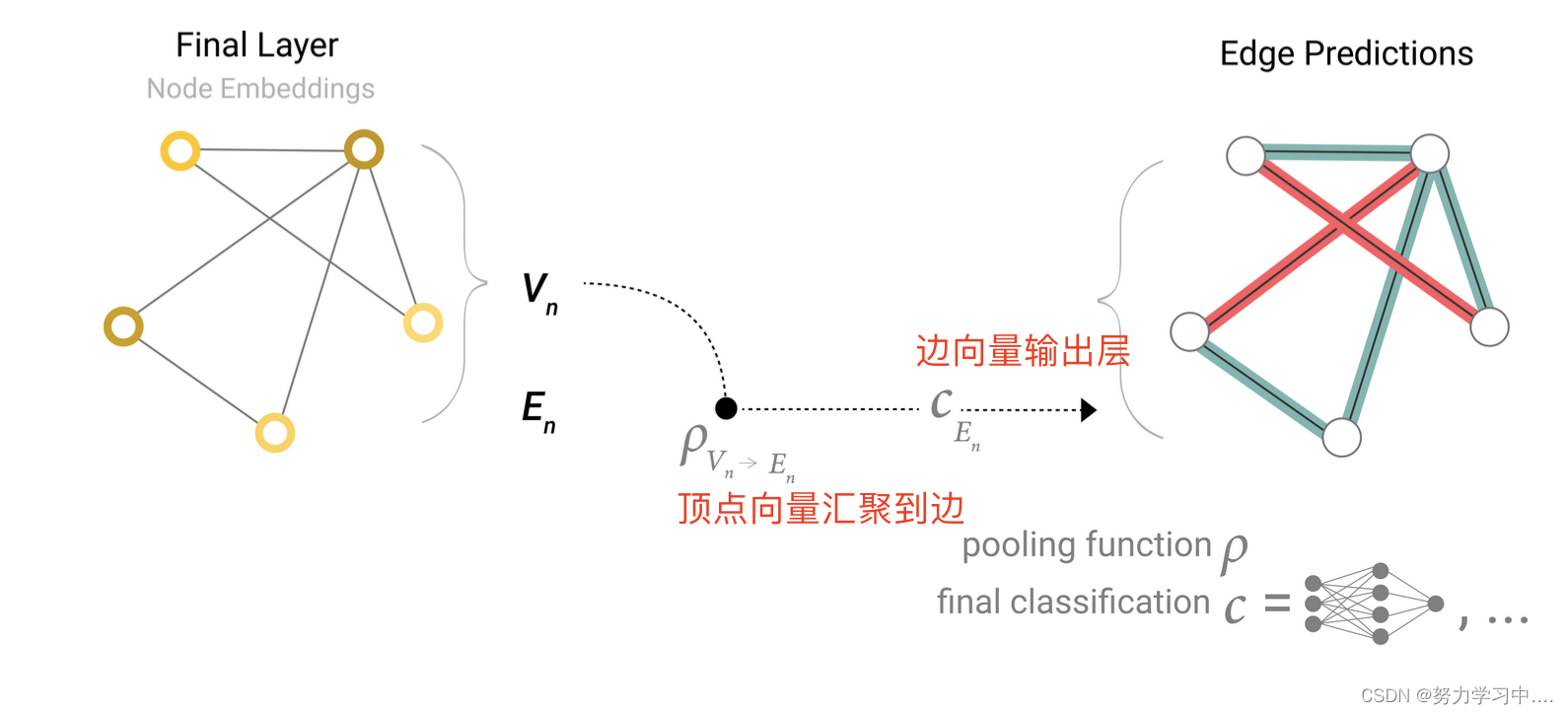
5. 得到全局输出层全局的输出,也可以用同样的方法(汇聚信息)
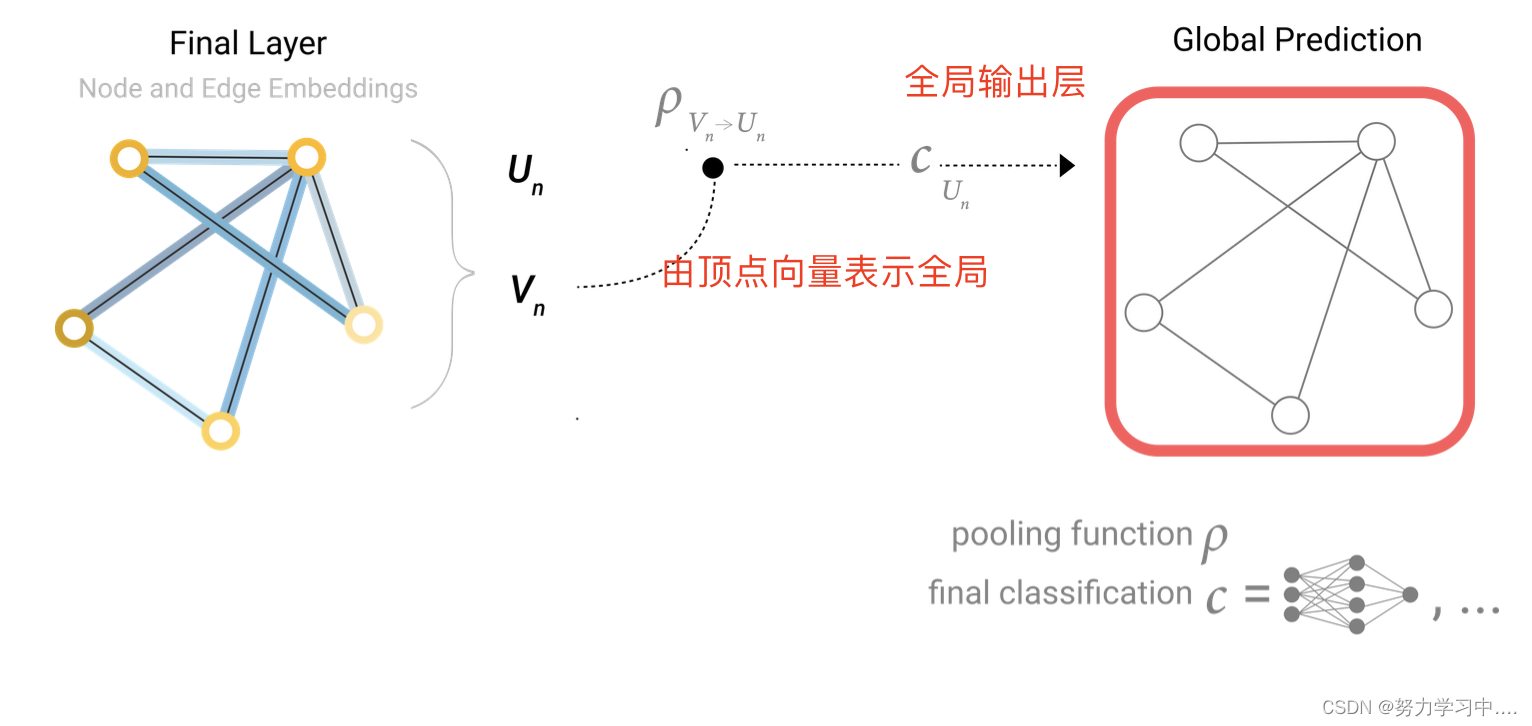
6. 最简单的GNN
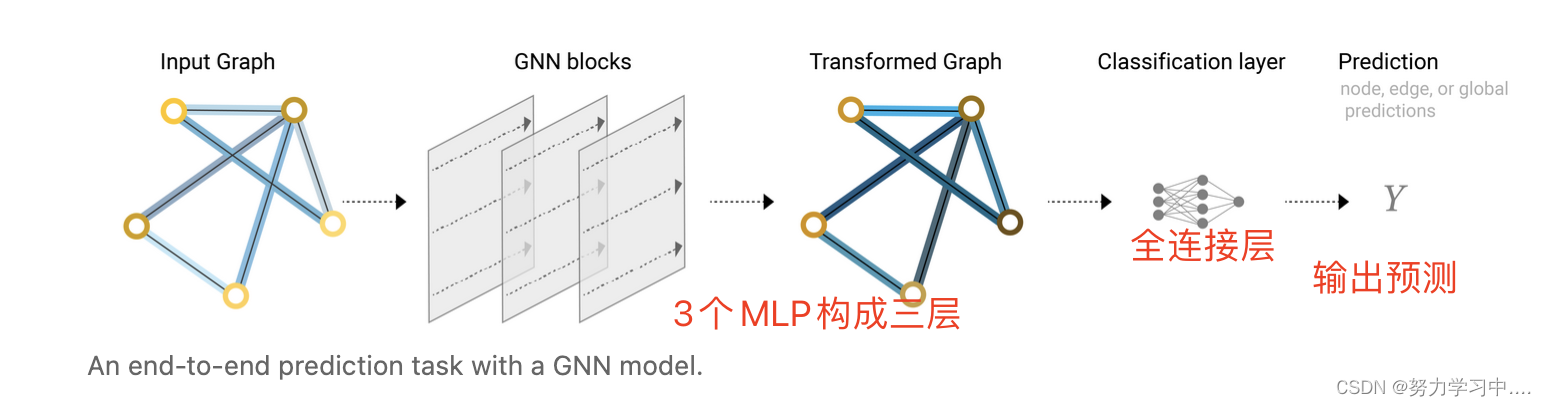
局限性: 在3个MLP处,并没有使用图的结构信息,没有考虑顶点的连接性;
没有合理的把整个图的信息更新到图的属性里面,导致最后结果不能反应图的信息。
7 信息传递(把图结构的信息考虑进去)
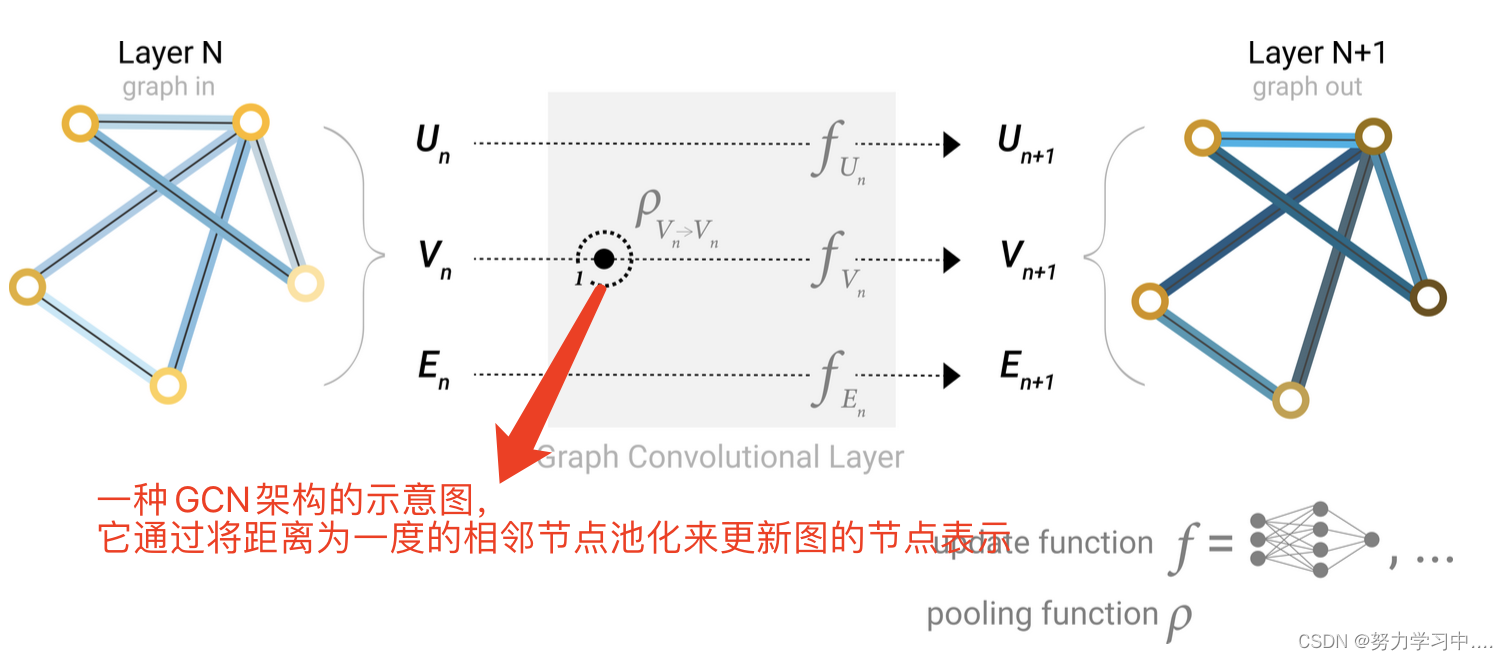
1. 比如在节点层面用MLP,这里不再使用单独的节点向量,而是把与该节点相连接的节点向量的信息汇聚到该节点上,得到向量的更新(得到进入MLP之前的向量),再放去MLP中
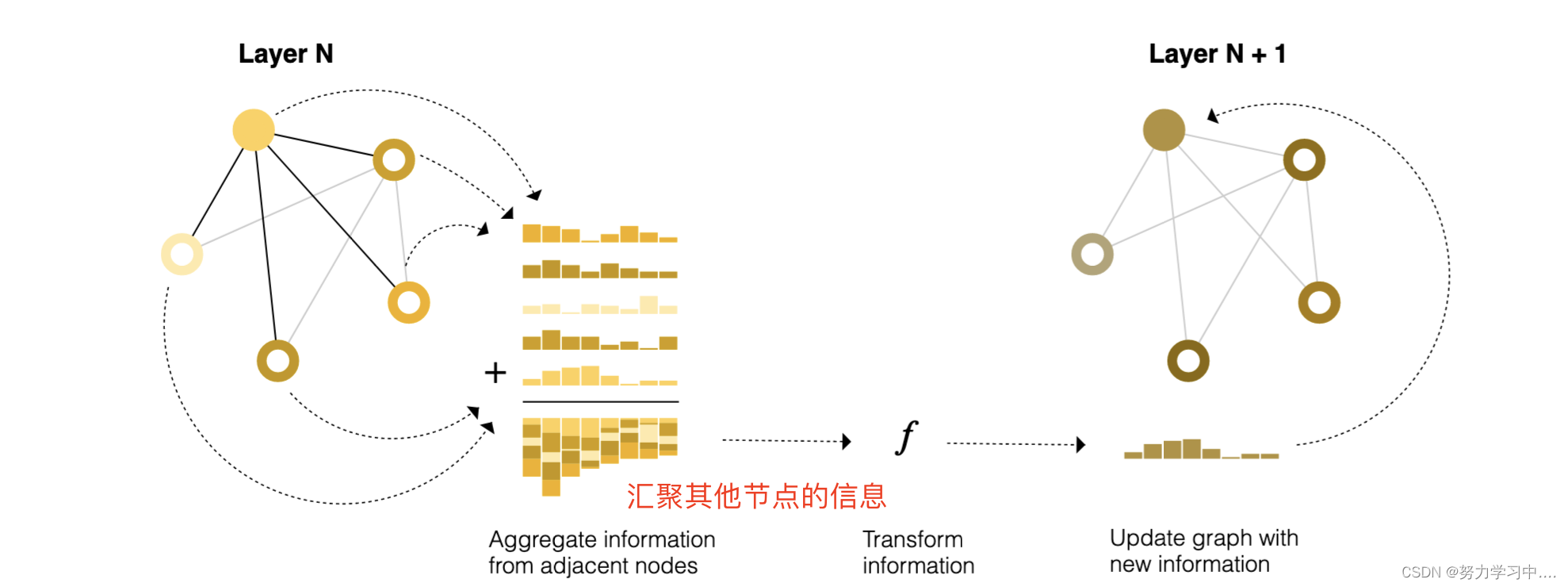
这里与图像的卷积类似,但不同的是,图像的卷积核窗口其权重是不同的,但这里加权和,这里只是加,权重是一样的;但是通道还是保留了;
2. 最简单的图神经网络操作,考虑步数为1 的节点
3. 顶点信息传递给边,边的信息传递给顶点
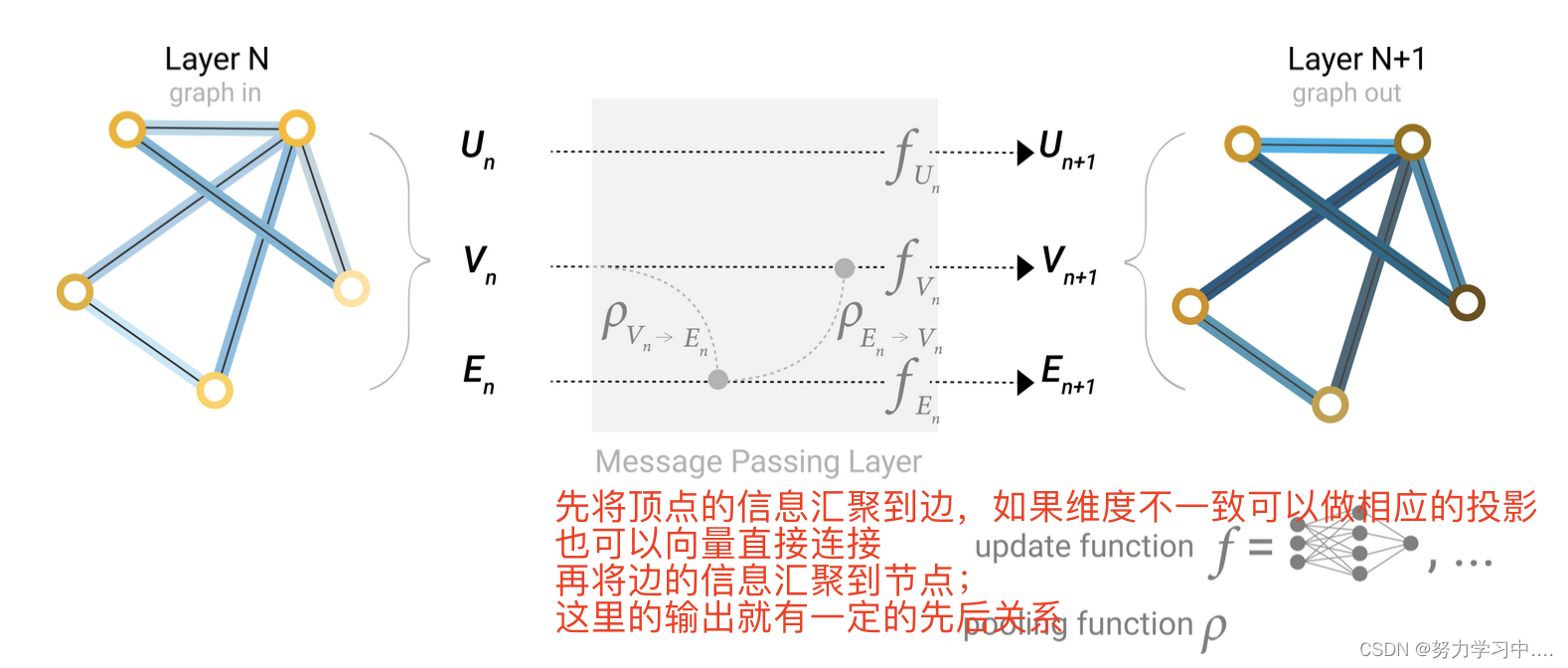
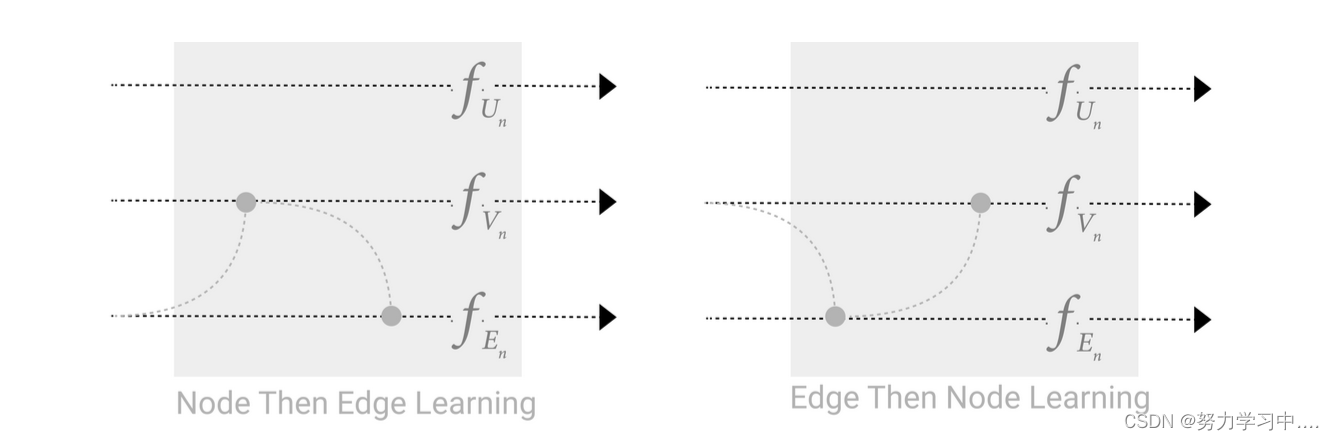
目前还没有结论,关于这个先后顺序会影响最后的结果;
4. 同时交替更新:(向量可能会宽一些,但不用考虑到底要先做哪一个):
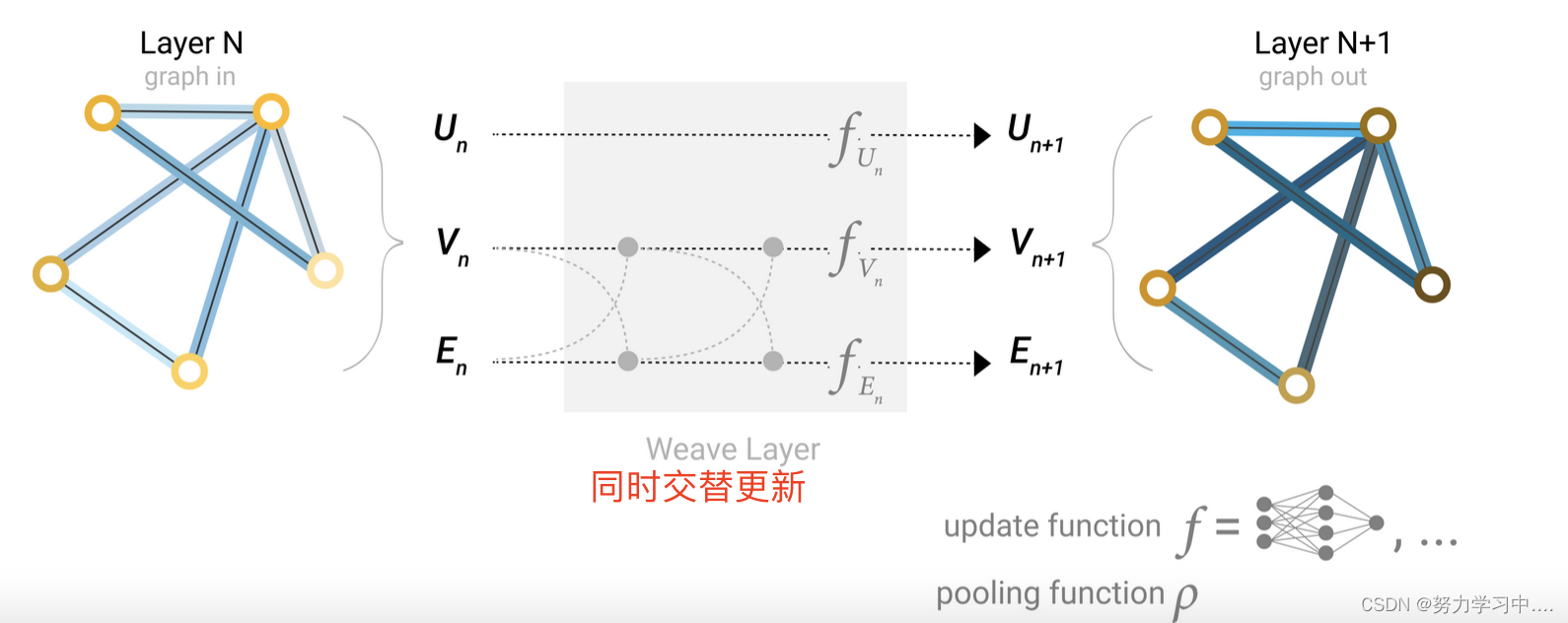
5. 全局信息该怎么做
每一次都只是看自己的邻接,但是图又很大,连接没有那么紧密,导致消息从一个点传递到很远的点,需要总很长的距离才可以;
解决方法: 加入master node或者context vector的东西,一个顶点与所有的顶点相连,一个顶点与所有的边相连(抽象的东西,就是全局信息)
如下图所示:
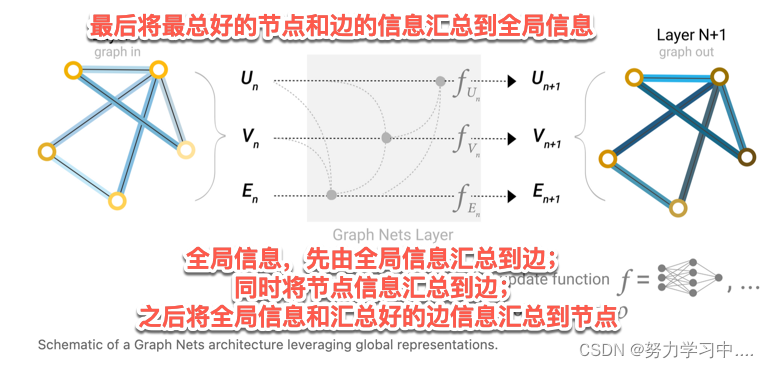
这样,我们就能学习到这三种向量;
而且这些向量在早期就开始进行消息传递;
8 GNN的playground
1. GNN程序嵌入到javascript中,调节参数,看到实际的训练效果;
可以在浏览器运行
2. 每个向量按元素做平均,或者按元素求Max(另外两种汇聚做法)
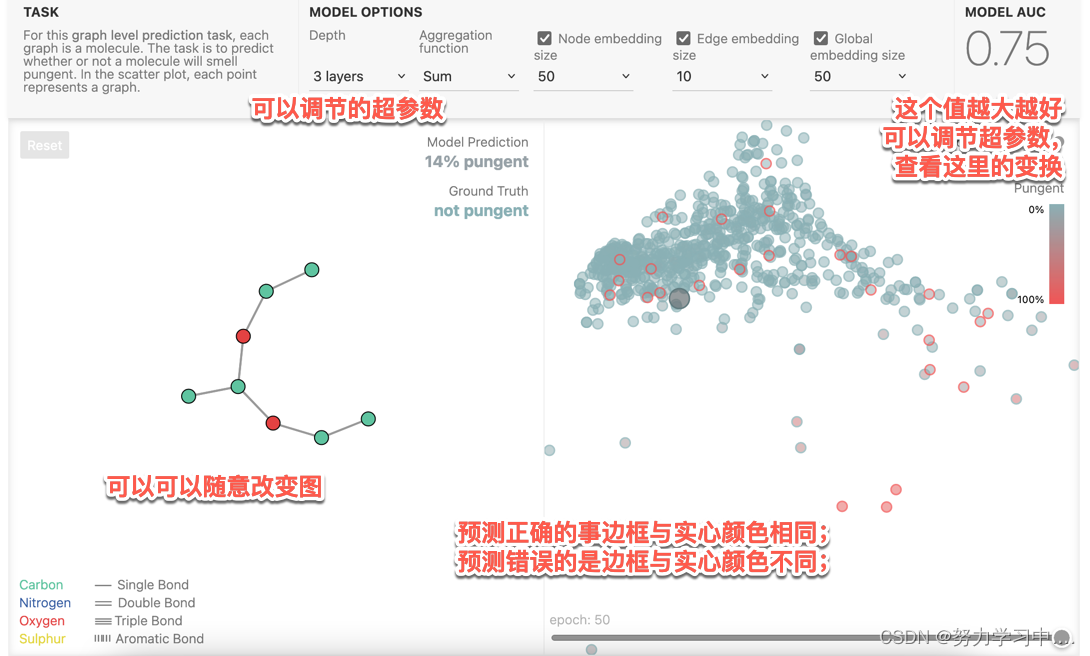
3. 不同超参数带来的模型性能展示:
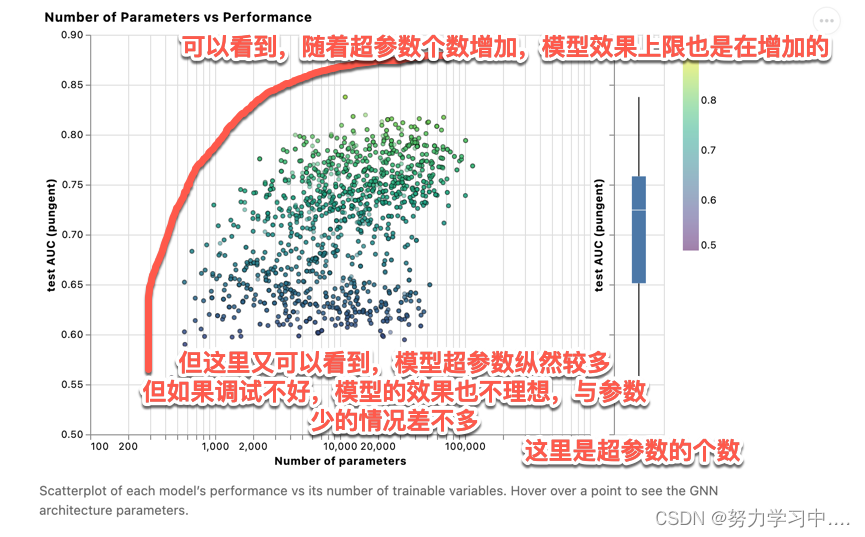
4. 来看具体的不同的超参数对模型效果的影响:
边、节点、全局的向量长度:
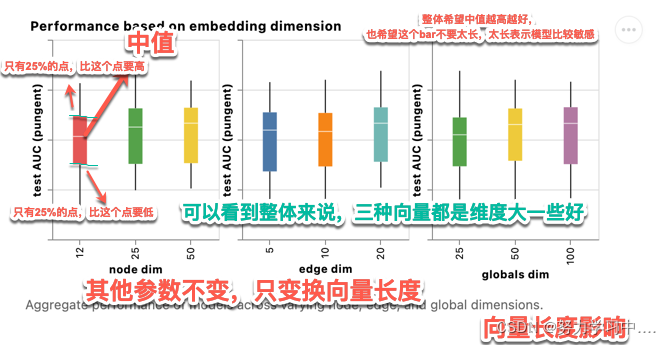
5. 层数改变对模型效果的影响:
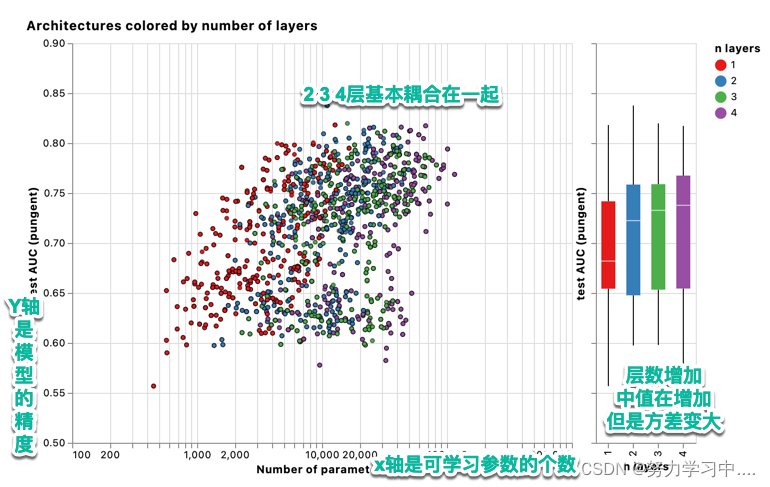
6. 聚合方法不同对模型效果的影响(求和/平均/最大):
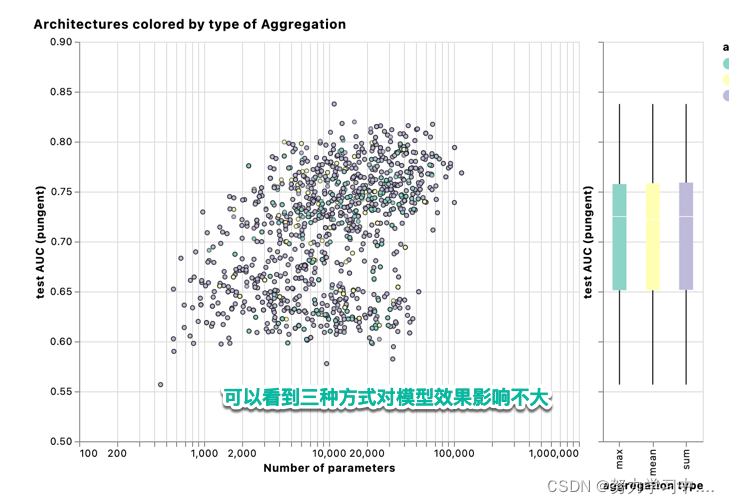
7. 在哪些属性之间传递信息对效果的影响:
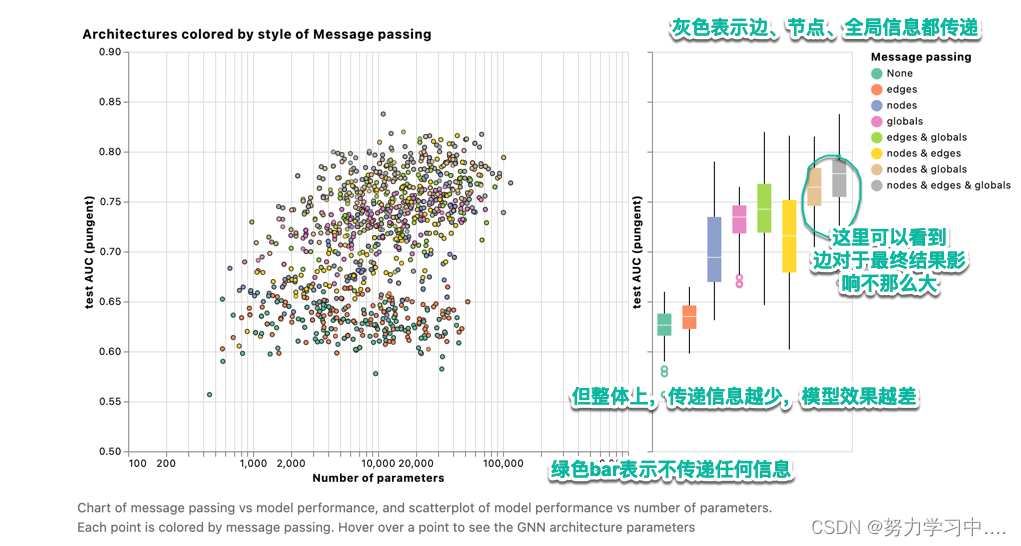
9 其他类型图
顶点之间有多种边
图可能是分层的,一个顶点下面可能有一个子图
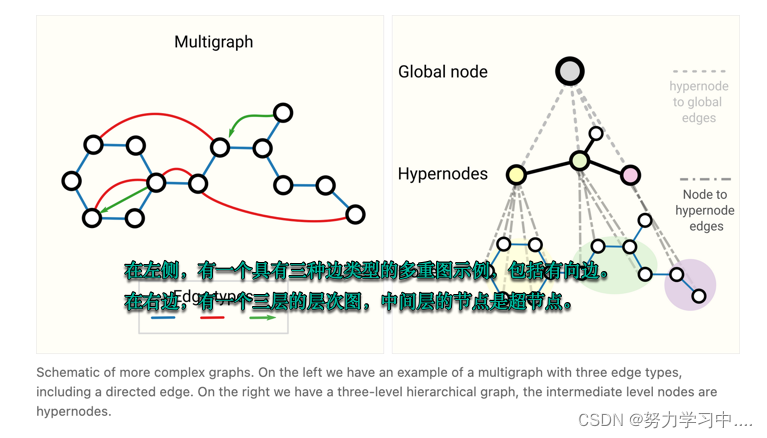
不同的图结构,在最后神经网络汇聚的时候会产生一定影响;
10 如何对图进行采样,或作batching
1. 对图进行采样,采样出小图出来再进行信息汇聚,算梯度时,把小图上中间结果记录下来就可;
做采样方法:
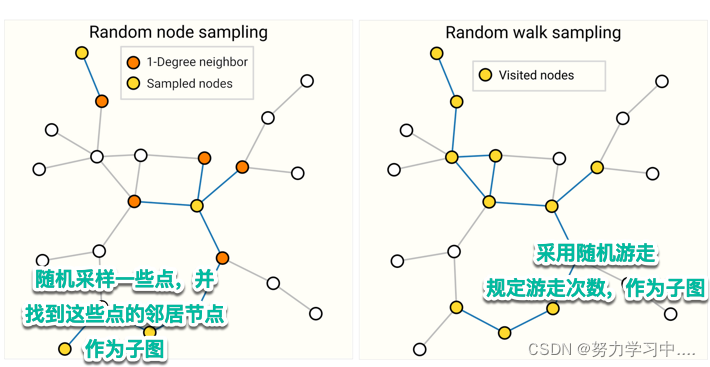
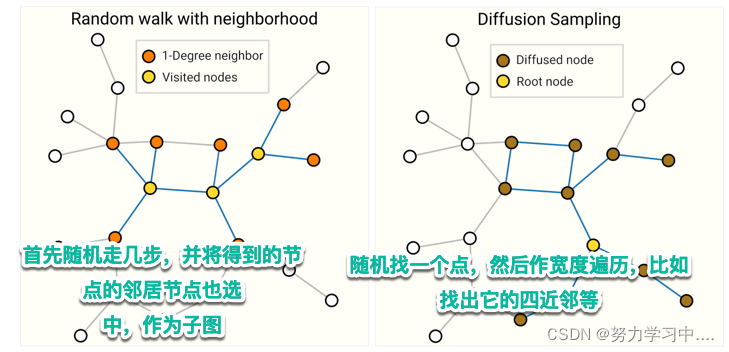
具体哪一种效果好,取决于图的结构;
不希望一个节点一个节点似得更新,希望作batch,多个节点更新,但是每个节点的邻居个数是不同的,如何将其合并为一个张量是一个挑战性的问题;
11 关于图的假设
1. CNN假设一种平移不变性,也就是说不够狗位于图像的哪个位置,他都是狗;
2. RNN假设的是网络按照顺序处理文字;
3. GNN的一个假设就是,在图的情况下,我们关心每个图组件(边、节点、全局)如何相互关联,因此我们寻找具有关系归纳偏差的模型,即模型应保留实体之间的显式关系(邻接矩阵)并保留图对称性(置换不变性)。
12 不同汇聚方法效果
没有特别理想的:
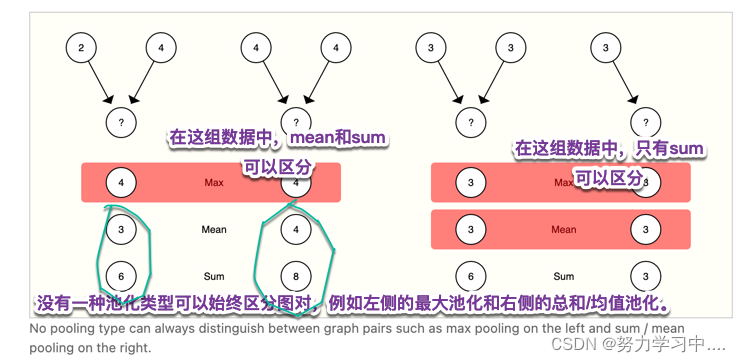
因此在实际应用中要根据图的实际情况选择聚合方法。
13 GCN
1. GCN--图卷积神经网络(带了汇聚信息的图神经网络),如果GCN有K个层,每一次都是看一个邻居;(后面这些部分作者都没有再详细介绍了)
等价于卷积神经网络中K层3*3的卷积,这样的话,每一个最后的顶点看到的是一个子图,子图大小是K,每过一层往前看了一步,最后那个点就是K步的信息的汇聚。
GCN就是用N这这样的子图,每个子图都往前走一步,然后将这些子图求一个embedding出来。
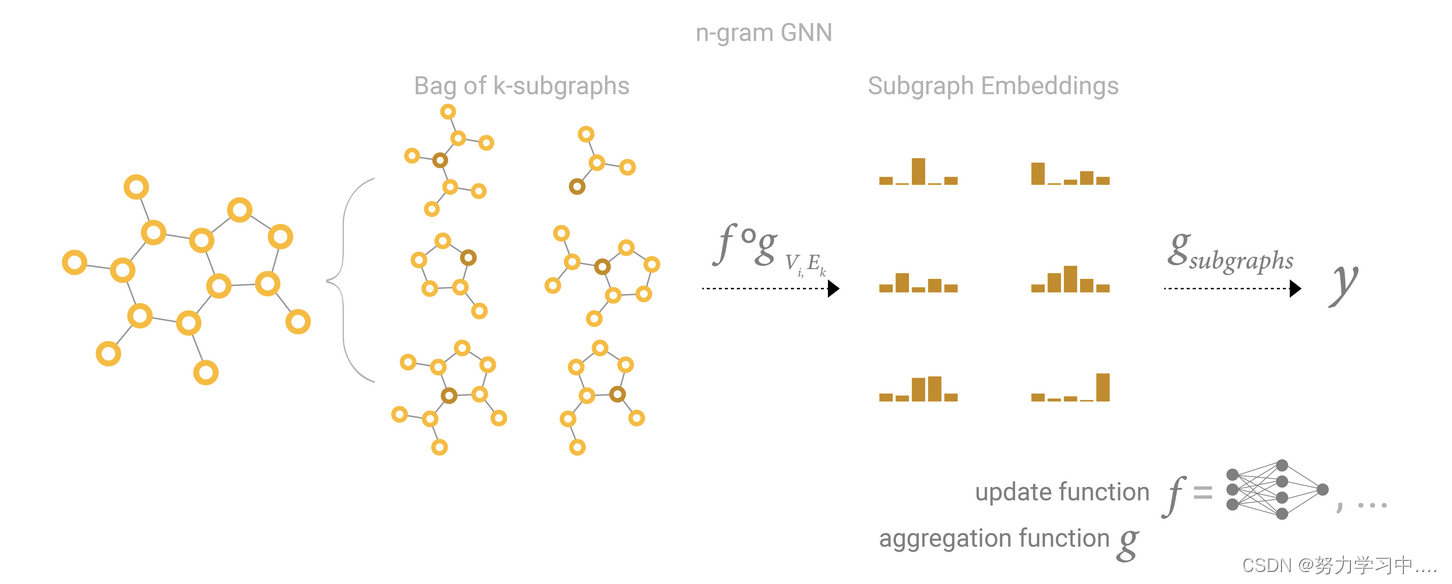
2. 可以将点和边做对偶(图论上,可以把点表示成边,边表示成点,然后邻接矩阵不变)
3. 在图上做卷积,或作random walk,相当于把图的邻接矩阵拿出来,作矩阵的乘法(类似于pagerank,邻接矩阵拿出来不断的做乘法)
图卷积作为矩阵乘法,矩阵乘法作为图上的游走;
4. 卷积和汇聚关系时,每个顶点和他邻接顶点权重加起来,
卷积是加权的和,卷积核的权重是与位置相关的;
在图上也可以做加权和,图上不用有位置信息,因为图上节点可以随意打乱顺序的,其连接的节点也不变,所以权重是对位置不敏感的,因此可以用类似attention的方法;
权重取决于两个节点向量的关系,不在是顶点的位置在什么地方,而是,两个顶点向量的关系,比如做点乘 ,再做softmax,作为attention后,每个顶点有一个权重,权重与顶点相乘,相加,得到一个GRaph Attention Neural Network;
5. 图的可解释性: 看看图到底学到什么信息,比如将子图提取出来,看其学到什么。
6. 图最后做完是不改变图的结构的,但想要生成图出来,怎样对图的结构进行有效建模;
14 总结
1. 先介绍什么是图,图应该用向量来表示;
2. 现实生活中数据如何表示成图,怎么用图做预测;
3. 机器学习算法用到图上,有什么挑战;
4. 定义GNN,就是对图上属性做变化,不改变图的属性;
5. 当属性有缺失如何做可以用聚合的操作;
6. 什么是真正意义上使用的GNN,顶点看邻接顶点,邻接边的信息;
7. 在整个层里面,如果能够把整个图的信息进行汇聚的话,可以对图的信息进行挖掘;
参考:A Gentle Introduction to Graph Neural Networks;
更多推荐
 已为社区贡献12条内容
已为社区贡献12条内容








所有评论(0)