KAN（Kolmogorov-Arnold Networks）模型详细说明

1. KAN 的背景

KAN 模型受 Kolmogorov-Arnold 表示定理的启发提出，作为多层感知机（MLP）的一种替代方案。与 MLP 固定激活函数的位置不同，KAN 将可学习的激活函数放置在网络的边缘（weights）上，完全摒弃了线性权重矩阵。通过这种设计，KAN 可以提高准确性和模型解释性。

2. 模型设计原理

1. Kolmogorov-Arnold 表示定理
   Kolmogorov 和 Arnold 证明了任意连续的多变量函数可以分解为若干单变量函数和加法运算的组合。具体表示为：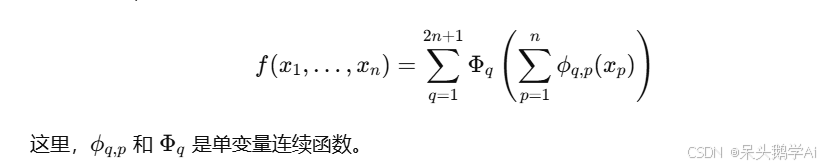

2. KAN 层的结构
   每一层 KAN 可以看作一个矩阵，其元素为单变量函数：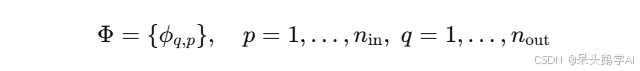

3. B样条（B-spline）激活函数
   KAN 使用 B样条函数作为单变量函数的参数化表示。这种方法可以通过调整控制点的密度，提高局部的精度。

4. KAN 的实现细节：1.残差激活函数: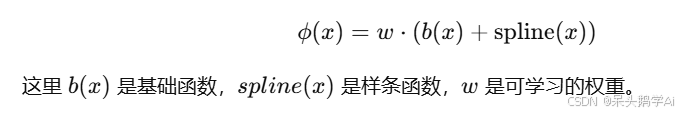2.初始化策略:激活函数初始时的样条部分趋近于 0，通过 Xavier 初始化确保稳定的学习过程。3.网格扩展：KAN 提供了动态调整样条网格密度的能力，可以通过加密网格点进一步提高拟合精度，而无需重新训练模型。

5.  KAN 的优势：1.准确性在数据拟合和偏微分方程求解任务中，KAN 显著优于 MLP。实验表明，具有较小参数的 KAN 可以达到与大型 MLP 相当甚至更高的准确性。2.泛化能力：KAN 能够很好地利用函数的组成结构，通过学习局部的单变量函数，解决了高维数据中的维度灾难问题。3.解释性：KAN 的激活函数可以直观地表示为样条函数，用户可以通过可视化的方法观察模型内部运行机制。

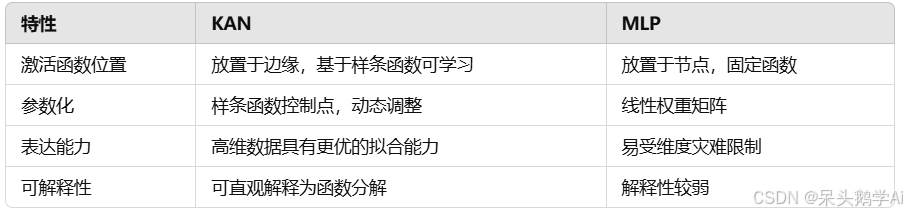
6. KAN 与 MLP 的对比

7. ---

   代码复现

8. 需要完整代码请私信或+q:3482637242