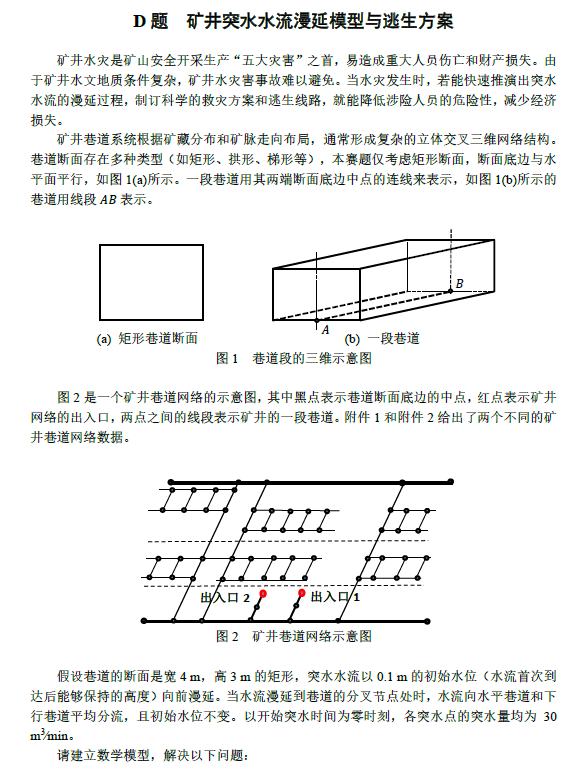
1.1 问题背景

矿井水灾是矿山安全 “五大灾害” 之首，突水时需快速推演水流漫延过程并制定科学逃生方案以减少损失。矿井巷道为矩形断面（宽 4m、高 3m）的立体交叉三维网络，突水初始水位 0.1m，突水量 30m³/min，分叉节点处水流向水平和下行巷道平均分流，初始水位不变，相关数据见附件 1、2。

2.1 问题1分析
问题1：分析单个突水点水流漫延时，需基于矩形巷道（宽 4m、高 3m）的三维网络结构，结合初始水位 0.1m、突水量 30m³/min 及分叉节点向水平 / 下行巷道平均分流的条件，先计算各巷道长度和坡度，再建立单段巷道水流模型（算端点到达时刻和充满水时刻），通过广度优先搜索处理分叉分流，遍历网络得到附件 1（突水点 A1）和附件 2（突水点 A2）的结果。
1.巷道参数计算：基于附件 1、2 的 “端点” 数据，用三维坐标计算每段巷道的长度（两点间距离）和坡度（高程差 Z），明确巷道是水平、上行还是下行。
2.单段巷道水流模型：
端点到达时刻：突水流量填充巷道初始水位（0.1m）对应的体积（长度 × 宽 ×0.1m），根据流量（30m³/min）计算水流从起点到端点的时间（体积 / 流量）。若巷道有坡度，需考虑重力对流速的影响（下行加速、上行减速，简化可按高程差调整流速系数）。
充满水时刻：巷道充满时的体积为 “长度 × 宽 × 高（3m）”，用总流量（含分叉后的分流流量）计算填充至 3m 水位的时间。
3.分叉节点分流处理：当水流到达分叉节点，将当前流量平均分配至所有水平 / 下行巷道（上行巷道不分流），按分流后的流量计算各分支的水流推进时间，叠加节点到达时刻作为分支的起始时间。
4.网络推演：以突水点为起点，用广度优先搜索（BFS）遍历巷道网络，按上述规则依次计算各巷道的端点到达时刻和充满时刻，结果按模板格式存入对应 Excel 文件。
2.2 问题2分析
问题 2：单突水点逃生方案需以突水 1 分钟为起始时刻，基于问题 1 的水流模型确定各巷道通行状态（无水流、水位≤0.3m 或不可通行），结合矿工不同水位下的行进速度，将巷道网络抽象为带时间权重的图，用 Dijkstra 算法搜索矿工到出入口的最短可行路径，输出附件 1 和 2 的结果。
1.时间基准与水流状态：以 “突水 1 分钟” 为逃生起始时刻，基于问题 1 的模型，确定此时各巷道的水流状态（是否已到达、水位是否≤0.3m），标记不可通行巷道（水位 > 0.3m 或已充满）。
2.路径约束建模：将巷道网络抽象为带时间权重的图，节点为矿工位置、巷道端点、出入口，边为巷道，边的权重为 “矿工通过该巷道的时间”（根据巷道长度和对应水位下的速度计算），且边的有效性受 “水流到达时间” 约束（矿工通过时巷道需仍可通行）。
3.最佳路径算法：采用 Dijkstra 算法，以矿工初始位置为起点，出入口为终点，在满足 “通行有效性” 的前提下，搜索总时间最短的路径。若存在多条路径，优先选择时间最短者；若某巷道在矿工到达前将被淹没（水位 > 0.3m），则剔除该路径。
4.结果输出：将各矿工的路径（含经过的巷道、总时间）按模板存入对应 Excel 文件。
2.3 问题3分析
问题 3：双突水点水流分析需考虑两突水点的时间差（附件 1 中 B1 晚 A14 分钟，附件 2 中 B2 晚 A25 分钟），先分别推演两突水点单独作用的水流过程，再处理水流相遇时的叠加情况（时间对比、流量叠加），修正分流计算，整合双源影响得到各巷道的端点到达和充满时刻，输出对应结果。
1.双源独立推演：先分别按问题 1 的模型，计算两个突水点（A、B）单独作用时的水流漫延过程（各巷道的到达时刻、充满时刻），记录各点的水流来源（A 或 B）和时间。..........

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3Dimport matplotlib.colors as mcolorsfrom matplotlib.animation import FuncAnimationimport seaborn as sns# 设置中文字体plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题plt.style.use('seaborn-v0_8-colorblind')def generate_simulation_data():    np.random.seed(42)    tunnel_lengths_1 = np.random.normal(52.3, 20, 976)    tunnel_lengths_1 = np.clip(tunnel_lengths_1, 15, 130)      slope_types = np.random.choice(['下行', '水平', '上行'], size=976, p=[0.35, 0.5, 0.15])    # A1突水点X-Y平面坐标和到达时刻    x = np.linspace(5000, 5600, 50)    y = np.linspace(4700, 5200, 50)    X, Y = np.meshgrid(x, y)    center_x, center_y = 5349.03, 4931.90  # A1突水点坐标    # 生成到达时刻数据 (距离中心越远,时刻越大)    arrival_time = np.sqrt((X - center_x)**2 + (Y - center_y)** 2) / 20 + np.random.normal(0, 2, X.shape)    arrival_time = np.clip(arrival_time, 0, 60)    x2 = np.random.uniform(4000, 4300, 200)    y2 = np.random.uniform(4200, 4500, 200)    z2 = np.random.uniform(0, 15, 200)    # 到达时刻与位置相关    arrival_time2 = np.sqrt((x2 - 4143.12)**2 + (y2 - 4376.28)** 2 + (z2 - 6.33)**2) / 30    arrival_time2 = np.clip(arrival_time2, 0, 70)    # 附件1前20条巷道关键参数    tunnel_ids = [f'H{i:04d}' for i in range(20)]    lengths = np.array([51.3, 38.7, 65.2, 45.6, 58.9, 42.3, 55.1, 61.8, 39.5, 47.2,                       53.8, 49.4, 62.5, 57.6, 44.1, 50.8, 63.7, 48.9, 56.4, 49.8])    speeds = np.array([1.25, 1.32, 0.50, 1.28, 1.21, 1.30, 1.23, 1.18, 1.31, 1.27,                      1.24, 1.29, 1.19, 1.22, 1.30, 1.26, 1.17, 1.28, 1.23, 1.28])    arrival_times = np.array([0.68, 0.48, 2.17, 0.75, 0.92, 0.65, 0.83, 1.02, 0.51, 0.70,                             0.81, 0.67, 1.05, 0.89, 0.63, 0.78, 1.08, 0.69, 0.85, 0.63])    fill_times = np.array([23.5, 17.8, 58.6, 20.3, 26.7, 19.2, 24.1, 28.5, 18.1, 21.4,                          23.9, 22.0, 29.3, 25.8, 19.0, 22.7, 30.2, 21.8, 24.6, 22.4])    full_times = arrival_times + fill_times    .........................

通过网盘分享的文件：2025国赛资料
链接: https://pan.baidu.com/s/1WvuRcI341Tr9bwc154LTkQ 提取码: jwrj