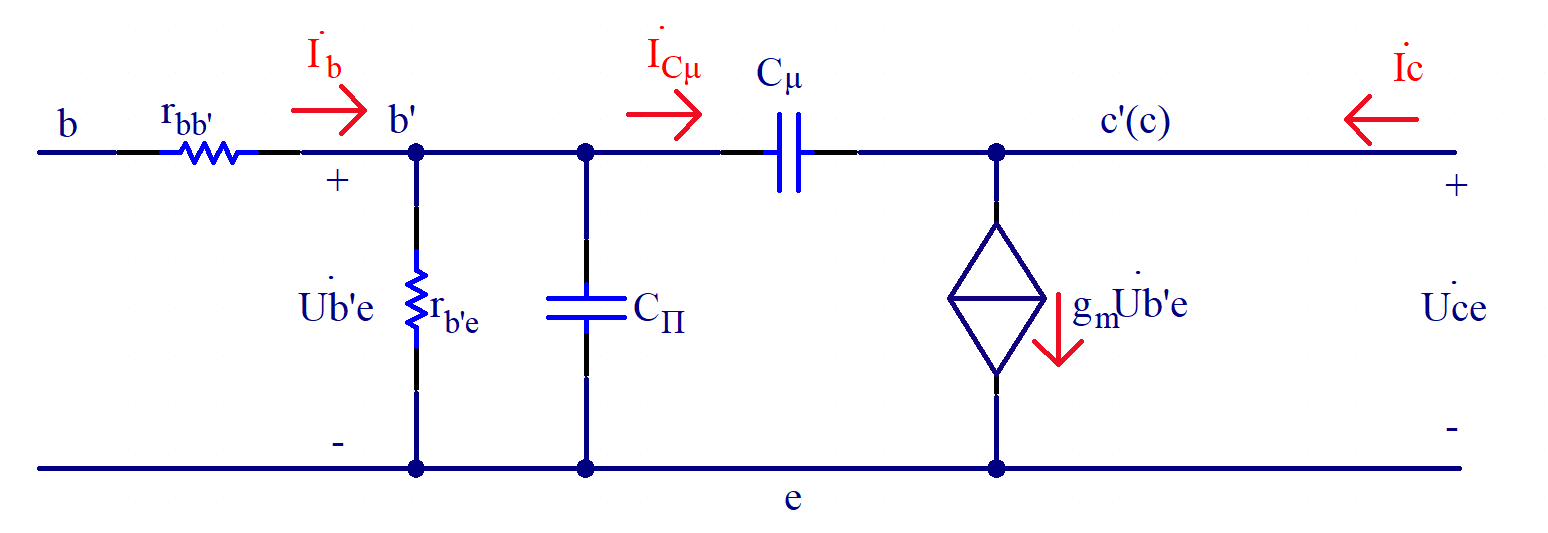
分析晶体三极管频率特性的等效模型
晶体三极管的H模型与Π模型BJT内部交流(动态)电阻电容示意图
晶体三极管的H模型与Π模型
- BJT内部交流(动态)电阻电容示意图

- 图中参数说明:
- 由于管子内集电区跟发射区的掺杂浓度高,rc,re非常小,可忽略不计,这样e’与e点可近似相等,c’与c也可近似相等。
- 基区体电阻rbb’
- 图中b’点是为分析方便而虚拟的基区内的等效基极。不同类型的BJT,rbb’的值相差很大,器件手册中常给出,在几十到几百欧之间。
- 电阻rb’e
- 发射结正偏电阻re折算到基极回路的等效电阻,即rb′e=(1+β)re=(1+β)VTIEQ r_{b^{'}e}=(1+\beta)r_{e}=(1+\beta) \frac{V_{T}}{I_{EQ}}rb′e=(1+β)re=(1+β)IEQVT
- 电容Cb’e’
- 发射结电容,由于BJT在放大区时发射结正偏,所以Cb’e主要是扩散电容,数值较大,对于小功率管,Cb’e在几十到几百皮法范围。
- 集电结电阻rb’c
- 在放大区内集电结处于反偏状态,因此rb’c的值很大,一般在100kΩ~10MΩ范围。
- 电容Cb’c’
- 主要是势垒电容,数值较小,在2~10pF范围内。
- 受控电流源
- 由于结电容影响,BJT中受控电流源不再受控于基极电流,因此不能βib表示。BJT工作在放大区,三个电极的电流实质上均受控于发射结上所加的电压,因此在高频小信号模型中,受控电流源该受vb’e控制的电流源。gm表明发射结电压对受控电流ic的控制能力,定义为:gm=∂ic∂vB′E∣VCE=ΔicΔvB′E∣VCEg_{m}=\frac{\partial i_{c} }{\partial v_{B'E}}\mid{_{V_{CE}}}=\frac{\Delta i_{c}}{\Delta v_{B'E}}\mid{_{V_{CE}}}gm=∂vB′E∂ic∣VCE=ΔvB′EΔic∣VCE
H参数等效模型
-
如下图,我们已知晶体管的H参数等效模型,注意rce相较于负载RL大,因此在进行H参数等效模型对交流态进行分析时,忽略不计。在H参数等效模型下,我们忽略的极间电容的影响,因此此模型适合中低频段的分析,无法分析高频。

-
由于rce相较于负载RL较大,我们分析时常常把rce等效为开路。

π参数等效模型
-
在此,对H参数等效模型进行分解,可得出如下的完整模型(接近物理模型,全频率段都适用):

-
现在,我们开始简化完整模型,去掉一些参数,rb’c 反偏电阻,锗管100kΩ,硅管500kΩ,较大,中可相当于断路,且rce如同H参数等效模型中一样,开路。
-
对Cμ进行戴维南等效,也称为Cμ的单向化等效,字面意思:从输入端看进去Cμ相当于等效电容Cμ’,从输出看进去相当于Cμ’’

-
求解Cμ’ ICμ˙=Ub′e˙−Uce˙XCμ=Ub′e˙−Uce˙1jwCμ\dot {I_{C_μ}}=\frac{\dot {U_{b'e}}-\dot {U_{ce}}}{X_{C_μ}}= \frac{\dot {U_{b'e}}-\dot {U_{ce}}}{\frac{1}{jwC_μ}}ICμ˙=XCμUb′e˙−Uce˙=jwCμ1Ub′e˙−Uce˙ XCμ′=1jwCμ′=Ub′eICμ X_{C'_μ}=\frac{1}{jwC'_{μ}}=\frac{U_{b'e}}{I_{C_μ}} XCμ′=jwCμ′1=ICμUb′e 令 K˙=Uce˙Ub′e˙\dot {K}=\frac{\dot{U_{ce}}}{\dot{U_{b'e}}}K˙=Ub′e˙Uce˙ 可得 Cμ′=(1−K˙)CμC'_{μ}=(1-\dot{K})C_{μ}Cμ′=(1−K˙)Cμ 可见,C’μ是变化的,且C’μ>Cμ,因为uce是负的,即k是负的。
-
求解C’'μ
- 推导公式
- C’'μ的容抗非常大。
-
Cπ与C’μ叠加的电路图下:C′Π=CΠ+Cμ′C^{'}{}_{Π}=C_{Π}+C^{'}_{μ}C′Π=CΠ+Cμ′

-
一般在数据手册中,我们可查到的参数有rbb’、Cob=Cμ、fT(特征频率),显然我们需要求解Cπ、gm、rb’e
求解gm、rb’e
- 首先求解rb’e,前面已经给出了等式,设中低频段放大倍数为β0:rb′e=(1+β0)re=(1+β0)UTIEQr_{b^{'}e}=(1+\beta _{0})r_{e}=(1+\beta _{0}) \frac{U_{T}}{I_{EQ}}rb′e=(1+β0)re=(1+β0)IEQUT
- 利用H参数与Π参数模型在中低频段等效这一特性,我们可知:IC˙IB˙=gmUb′e˙Ub′e/rb′e=gmrb′e=β0\frac{\dot{I_{C}}}{\dot{I_{B}}}=\frac{g_{m}\dot{U_{b'e}}}{U_{b'e}/r_{b'e}}=g_{m}r_{b'e}=\beta _{0}IB˙IC˙=Ub′e/rb′egmUb′e˙=gmrb′e=β0 得 gm=β0rb′e=β0(1+β0)UTIEQg_{m}=\frac{\beta _{0}}{r_{b'e}}=\frac{\beta _{0}}{(1+\beta _{0})\frac{U_{T}}{I_{EQ}}}gm=rb′eβ0=(1+β0)IEQUTβ0
求解Cπ且β的频响
- 定义:β˙=IC˙IB˙∣UCE\dot {\beta}=\frac{\dot{I_{C}}}{\dot{I_{B}}}\mid _{U_{CE}}β˙=IB˙IC˙∣UCE
- 在高频等效电路模型中,CE之间无电压变化,可以理解为很大的C’'μ短路了:

- 可得:β˙=IC˙IB˙=gmUb′e˙Ub′e˙rb′e+Ub′e˙XCπ′=gm(1rb′e+jwCπ′)=gmrb′e1+jwrb′eCπ′=β01+jwrb′eCπ′\dot {\beta}=\frac{\dot{I_{C}}}{\dot{I_{B}}}=\frac{g_{m}\dot{U_{b'e}}}{\frac{\dot{U_{b'e}}}{r_{b'e}}+\frac{\dot{U_{b'e}}}{X_{C^{'}_{π}}}}=\frac{g_{m}}{(\frac{1}{r_{b'e}}+jwC^{'}_{π})}=\frac{g_{m}r_{b'e}}{1+jwr_{b'e}C^{'}_{π}}=\frac{\beta _{0}}{1+jwr_{b'e}C^{'}_{π}}β˙=IB˙IC˙=rb′eUb′e˙+XCπ′Ub′e˙gmUb′e˙=(rb′e1+jwCπ′)gm=1+jwrb′eCπ′gmrb′e=1+jwrb′eCπ′β0
- 显然这是一个低通滤波器的等式,令fβ=12πrb′eCπ′f_{\beta }=\frac{1}{2πr_{b'e}C^{'}_{π}}fβ=2πrb′eCπ′1 原式等于: β˙=β01+j(ffβ)\dot{\beta}=\frac{\beta _{0}}{1+j(\frac{f}{f_{\beta}})}β˙=1+j(fβf)β0
- 波特图

- 当f=fT时,|β|=1,可得fTfβ≈β0\frac{f_{T}}{f_{\beta}}\approx \beta _{0}fβfT≈β0 即 fβ=fTβ0=12πrb′eCπ′f_{\beta}=\frac{f_{T}}{\beta _{0}}=\frac{1}{2πr_{b'e}C^{'}_{π}}fβ=β0fT=2πrb′eCπ′1 得 Cπ′=β02πrb′efTC^{'}_{π}=\frac{\beta _{0}}{2πr_{b'e}f_{T}}Cπ′=2πrb′efTβ0
- 前面已知:C′π=Cπ+Cμ′C^{'}{}_{π}=C_{π}+C^{'}_{μ}C′π=Cπ+Cμ′ 而 Cμ′=(1−K˙)CμC'_{μ}=(1-\dot{K})C_{μ}Cμ′=(1−K˙)Cμ K˙=Uce˙Ub′e˙\dot {K}=\frac{\dot{U_{ce}}}{\dot{U_{b'e}}}K˙=Ub′e˙Uce˙ 此时 Ub′e˙=0(短路)\dot{U_{b'e}}=0(短路)Ub′e˙=0(短路)因此C′π=Cπ+CμC^{'}{}_{π}=C_{π}+C_{μ}C′π=Cπ+Cμ
- C’π已知(上式求解),Cμ已知(手册给出),即可求出Cπ。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)