中国人口老龄化趋势的加剧，2022年首次出现人口负增长，说明中国未来将将出现人口下降的趋势。这一趋势必然会影响许多城市的高质量和可持续发展特别是次要城市和地下城市，其影响可能是多方面的。与此同时，全球极端气候事件的日益频繁和租金经济低迷将给城市发展的弹性带来前所未有的挑战 通过网络爬虫和实地研究的结合，我们获得了城市1和城市2在特定一天的待售属性的基本信息，如附录1和2所示。此外，附录3和附件4提供了城市1和城市2中一个特定年份的一些基本服务的POI数据。请使用这些数据对以下四个问题进行具体的优化和建模。

问题一： 考虑到上述数据和可以在互联网上收集的数据，你是否可以对城市1和城市2的未来房价进行具体预测，以及对现有住房总量进行具体估计?

为了解决问题一，我们将通过数学建模方法预测城市1和城市2的未来房价，并估计现有住房总量。下面详细说明模型的建立、数据的预处理、特征提取、预测算法和相应公式。

1. 数据预处理与特征提取 首先，我们对原始数据进行清洗和预处理，提取关键特征用于建模。具体来说，每个城市的待售属性数据包含多个特征，记作以下变量： P：房价（每平方米价格） H：总住户数量 G：绿化率 F：容积率（建筑面积与用地面积的比率） M：物业管理费（单位面积月管理费） A：地上停车费（月费） U：地下停车费（月费） 设数据样本为n条，每条数据对应一个待售物业的特征向量 (Pi,Hi,Gi,Fi,Mi,Ai,Ui)，其中 i=1,2,…,n。 数据清洗 在实际建模中，我们先移除缺失值，以确保模型在完整的数据上训练。假设我们保留的数据集记作 D⊂R7，表示清洗后的样本数据，其中包含 m≤nm \leq n条样本。 2. 房价预测模型 我们选择使用回归模型来预测未来房价。考虑到房价与其他特征的关系非线性，我们采用随机森林回归（Random Forest Regression）模型。模型设定如下： 随机森林回归模型的数学表达 随机森林回归由多棵回归树构成，每棵树对数据的不同子集进行训练。具体公式如下： 对每棵决策树 Tj，从数据集 D中有放回地采样，生成子集 Dj。 每棵决策树基于特征划分数据并构建节点，树的输出为叶节点上样本的平均房价预测。 令随机森林模型包含N 棵树，模型输出为：

 

其中，x=(H,G,F,M,A,U)是输入特征向量，P^是模型的预测房价。 3. 误差评估 模型的误差使用均方根误差（Root Mean Square Error, RMSE）进行衡量。RMSE定义如下：

 

其中，Pi是实际房价，P^i是模型的预测房价，m是测试集样本数量。 4. 现有住房总量估算 现有住房总量估算是通过总住户数量计算的。假设每个社区的总住户数量 HHH 代表社区内住房的实际分布情况，则总住房量可以表示为所有社区住户数量的总和。 设社区数为k，第j个社区的总住户数为 Hj，则城市的总住房量T表示为：

 

5. 空间分布建模 为展示城市的住房密度分布，我们采用住房密度图，通过各个社区的经纬度坐标可视化总住户数量。设每个社区的经度和纬度分别为 lonj 和 latj，其住房密度大小表示为总住户数量Hj​。 密度函数：对于空间分布，可使用高斯核函数K表示一个社区的住房密度。其密度函数为：

 

其中K为核函数，(x,y)为地图上的任意坐标点。此公式展示了每个社区的住房分布对整个城市的影响范围。 6. 模型预测与应用 特征对房价的影响 房价预测依赖于多种因素，具体地，房价与住户数量、绿化率、容积率、管理费用、停车费用等特征存在一定的关系。特征权重可以通过随机森林模型训练后计算特征重要性，以定量表示每个特征对房价的影响。 设特征权重为 wH,wG,wF,wM,wA,wU，则预测房价的线性组合可表示为：

 

在随机森林模型中，通过多树投票得到最终房价预测。 未来房价预测 在得到当前房价预测模型后，可以结合时间序列模型（如ARIMA或LSTM）进一步进行房价的时间序列预测。设当前预测房价为P^t​，未来的房价预测为：

 

其中 ΔP表示价格变化的增量，f是时间序列模型。 时间序列房价预测 在时间序列预测中，房价的变化趋势通常可以通过自回归积分滑动平均模型（ARIMA）建模。设房价增量序列为 ΔPt=Pt−Pt−1，则ARIMA模型为：

 

其中，c为常数，ϕ为自回归系数，θ为移动平均系数，ϵ为随机误差项。 问题一结果：

 

问题二请对城市1和城市2的不同部门的服务水平进行定量分析，提取这两个城市的共性和独特性，以及它们各自的优缺点。

为完成问题二的数学建模，我们将城市1和城市2的不同部门服务水平进行定量分析，以提取这两个城市的共性和独特性，并找出其优缺点。以下将详细说明分析过程、数学公式以及模型构建。

1. 问题描述与目标 城市1和城市2各包含多个服务部门，我们的目标是对不同部门的服务水平进行定量分析。通过计算各部门服务数量和占比，提取城市1和城市2的服务共性和差异。此外，分析这两个城市各自的优缺点。

2. 数据准备 设两个城市的部门数据文件为 D1,D2,…,Dn，其中n 为部门数量。每个文件包含某部门的服务点数量。我们记： Si,j：城市i 中部门j 的服务数量。 Ti：城市i 的总服务数量，计算公式为：

 

其中 i=1,2，表示城市1和城市2。

1. 各部门服务水平的定量分析 我们首先计算每个部门在城市中的服务数量，以确定其绝对水平。服务数量越高，通常表示该部门服务覆盖范围越广。 部门服务数量的计算 每个部门的服务数量 Si,j已知，我们计算各部门的服务数量向量 Si=[Si,1,Si,2,…,Si,n]。

2. 服务数量占比的计算 为了定量比较两个城市各部门的相对服务水平，我们将每个部门的服务数量标准化为总服务数量的百分比。这种标准化允许跨城市的服务水平比较。 对于城市i中部门j的服务占比，定义如下：

 

其中 Pi,j表示城市 i中部门 j的服务数量占比。 各部门服务占比向量 我们定义每个城市的服务占比向量 Pi=[Pi,1,Pi,2,…,Pi,n]，其中 i=1,2。这两个向量分别表示城市1和城市2各部门的相对服务水平。

1. 共性与差异分析 为分析两个城市的共性和差异，我们计算每个部门的服务占比差异。定义差异向量 D=[D1,D2,…,Dn]，其中 Dj表示城市1和城市2在部门j的服务占比差异，计算公式为：

 

其中： 若 Dj>0，则城市1在部门 j上的服务占比高于城市2，表示该部门可能为城市1的服务优势； 若 Dj<0，则城市2在部门 j上的服务占比高于城市1，表示该部门可能为城市2的服务优势。

1. 优缺点提取 基于服务占比差异，我们可以识别出每个城市的优缺点。具体步骤如下： 优势部门：对于城市1，我们选择 Dj>0且值较大的部门作为优势部门。同样，对于城市2，我们选择 Dj<0且值较小的部门作为其优势部门。即：

 

劣势部门：劣势部门则为服务占比相对较低的部门。对城市1，选择 Dj<0的部门；对城市2，选择 Dj>0的部门。 优缺点矩阵 为了方便提取优缺点，我们可以构建优缺点矩阵 A，其中每个元素 ai,j 表示城市 i在部门 j的优势（1）或劣势（-1），具体定义为：

 

通过矩阵 A，我们可以直接得到每个城市的优缺点分布。

 

1. 定量可视化

为了直观展示分析结果，我们构建以下两类图表：

服务数量柱状图：以各部门的绝对服务数量为依据，绘制城市1和城市2的服务水平对比图，用于展示绝对服务覆盖水平。

对于城市i和部门j，服务数量柱状图中的每根柱子高度为 Si,j。

 

服务占比柱状图：以各部门的服务占比为依据，绘制各部门相对服务水平对比图，用于观察各城市的服务优势与劣势。

对于城市i 和部门 j，服务占比柱状图中的每根柱子高度为 Pi,j。

 

问题三 利用附录3和附件4中的数据，评估这两个城市应对极端天气和紧急情况的弹性，并定量评估这两个城市的可持续发展能力。你的模型应该明确地确定这两个城市的特定弱点，需要未来发展的关键领域，以及在有限的财政资源的限制下的长期和长期终止投资计划。

 

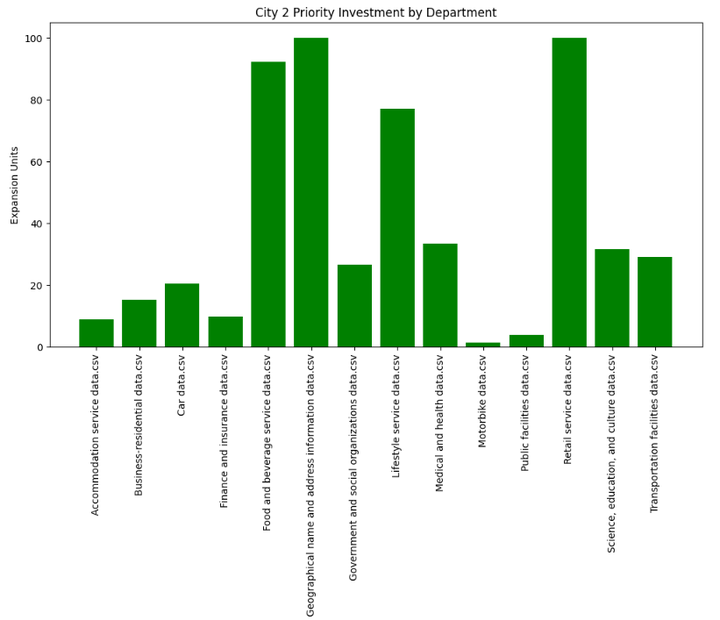
问题四：根据以上分析，起草两个城市未来发展规划，不超过两次。该计划应明确概述主要的投资项目、投资金额以及智慧城市发展水平的预期改善。

完整思路代码↓