腐蚀

定义
腐蚀目标是使目标区域ROI范围“变小”，其实质造成图像的边界收缩，可以用来消除小且无意义的目标物。作用是消除背景的小颗粒噪声。其公式表达式子为：
$$A\ominus B=\cap b\in B{A}_{-b}$$

伪代码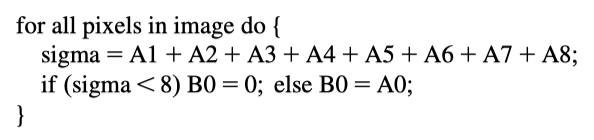

膨胀

定义
膨胀的目标是使目标区域ROI范围“变大”，将于目标区域接触的背景点合并到该目标物中，使目标边界向外部扩张。作用就是可以用来填补目标区域中某些空洞以及消除包含在目标区域中的小颗粒噪声。 其公式表达式子为：
$$A\oplus B={\cup }_{b\in B}{A}_b$$

伪代码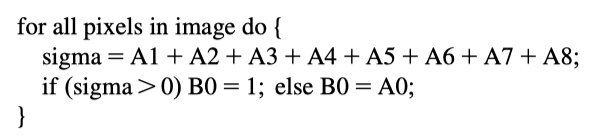

腐蚀和膨胀算子的运算法则

重要定理
$$\begin{array}{rl}& (A\ominus B{)}^{\mathrm{c}}=A^{\mathrm{c}}\oplus B^{\mathrm{r}}\\ & (A\oplus B{)}^{\mathrm{c}}=A^{\mathrm{c}}\ominus B^{\mathrm{r}}\end{array}$$
其中$A^{\mathrm{c}}$表示集合$A$的补集，$B^{\mathrm{r}}$表示集合$B$相对与其集合原点的反射（镜像）。

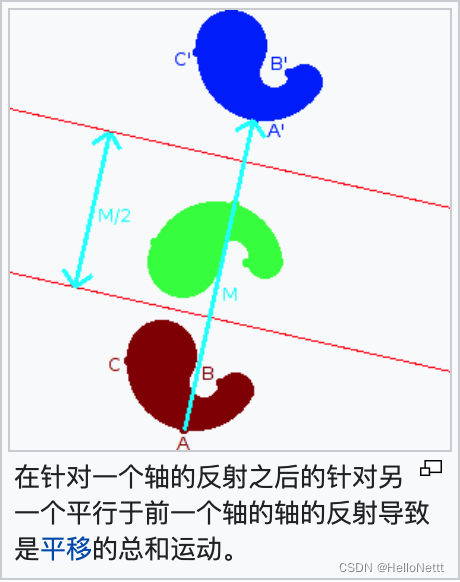
基本性质
$$\begin{gathered} (A\oplus B)\oplus C=A\oplus (B\oplus C) \\ (A\ominus B)\ominus C=A\ominus (B\oplus C) \end{gathered}$$
$$X\oplus Y=Y\oplus X$$
$$\begin{array}{rl}& (A\oplus B)\oplus C=(A\oplus C)\oplus B\\ & (A\ominus B)\ominus C=(A\ominus C)\ominus B\end{array}$$
$$\begin{array}{rl}& A\oplus (B\cup C)=(A\oplus B)\cup (A\oplus C)\\ & A\ominus (B\cup C)=(A\ominus B)\cap (A\ominus C)\\ & (A\cap B)\ominus C=(A\ominus C)\cap (B\ominus C)\\ & A\ominus (B\cap C)\supseteq (A\ominus B)\cup (A\ominus C)\end{array}$$

闭运算

闭运算就是先膨胀再腐蚀
$$A\cdot B=(A\oplus B)◯B$$

开运算

开运算就是先腐蚀再膨胀
$$A\circ B=(A\ominus B)\oplus B$$

闭运算和开运算的运算法则

重要定理
$$\begin{array}{rl}& (A\cdot B{)}^{\mathrm{c}}=A^{\mathrm{c}}\circ B^{\mathrm{r}}\\ & (A\circ B{)}^{\mathrm{c}}=A^{\mathrm{c}}\cdot B^{\mathrm{r}}\end{array}$$
其中$A^{\mathrm{c}}$表示集合$A$的补集，$B^{\mathrm{r}}$表示集合$B$相对与其集合原点的反射（镜像）。

基本性质
$$\begin{gathered} (A\cdot B)\cdot B=A\cdot B \\ (A\circ B)\circ B=A\circ B \end{gathered}$$
$$\begin{gathered} (A\oplus B)\circ B=(A\oplus B) \\ (A\ominus B)\cdot B=(A\ominus B) \end{gathered}$$
$$\begin{array}{rl}& A\oplus D\supseteq A\cdot D\supseteq A\\ & A\ominus D\subseteq A\circ D\subseteq A\end{array}$$