机器学习：关联与回归

本文深入探讨数据挖掘与机器学习中的两大核心技术：关联规则挖掘与回归分析，涵盖从基础理论到实际应用的完整知识体系。

燕双嘤

1963人浏览 · 2020-04-13 12:38:19

燕双嘤 · 2020-04-13 12:38:19 发布

1，Apriori算法

1.1，关联

关联规则：关联规则反映一个事物与其他事物之间的相互依存性和关联性。如果两个或者多个事物之间存在一定的关联关系，那么，其中一个事物就能够通过其他事物预测到。

$A\Rightarrow B$

关联规则可以看作是一种IF-THEN关系。假设商品A被客户购买，那么在相同的交易ID下，商品B也被客户挑选的机会就被发现了。

【例子】有没有发生过这样的事：你出去买东西，结果却买了比你计划的多得多的东西？这是一种被称为冲动购买的现象，大型零售商利用机器学习和Apriori算法，让我们倾向于购买更多的商品。购物车分析是大型超市用来揭示商品之间关联的关键技术之一。他们试图找出不同物品和产品之间的关联，这些物品和产品可以一起销售，这有助于正确的产品放置。买面包的人通常也买黄油。零售店的营销团队应该瞄准那些购买面包和黄油的顾客，向他们提供报价，以便他们购买第三种商品，比如鸡蛋。因此，如果顾客买了面包和黄油，看到鸡蛋有折扣或优惠，他们就会倾向于多花些钱买鸡蛋。这就是购物车分析的意义所在。

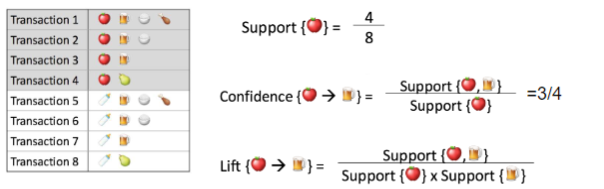
置信度：表示你购买了A商品后，你还会有多大的概率购买B商品。

$Confidence=\frac{freq(A,B)}{freq(A)}$

支持度：指某个商品组合出现的次数与总次数之间的比例，支持度越高表示该组合出现的几率越大。

$Support=\frac{freq(A,B)}{N}$

提升度：提升度代表商品A的出现，对商品B的出现概率提升了多少，即“商品 A 的出现，对商品 B 的出现概率提升的”程度。

$Lift=\frac{Support}{Support(A)\times Support(B)}$

1.2，Apriori算法思想

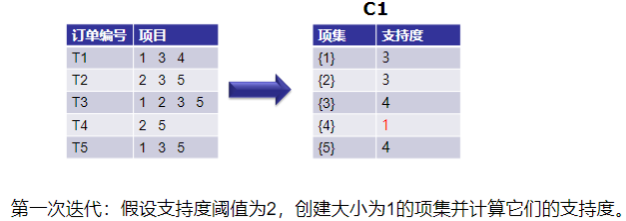
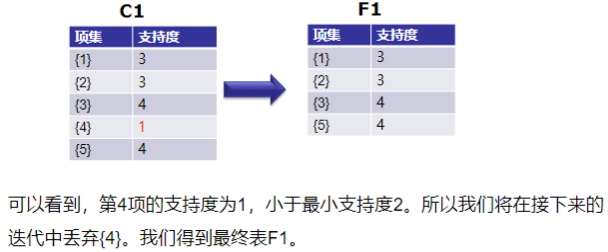
Apriori算法利用频繁项集生成关联规则。它基于频繁项集的子集也必须是频繁项集的概念。频繁项集是支持值大于阈值（support）的项集。

Apriori算法就是基于一个先验：如果某个项集是频繁的，那么它的所有子集也是频繁的。

算法流程：
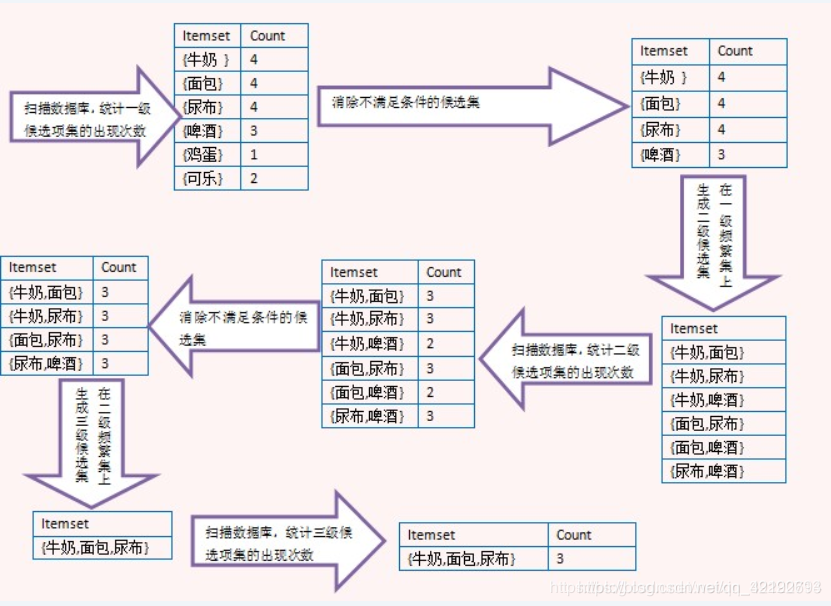
输入：数据集合D，支持度阈值𝛼
输出：最大的频繁k项集
    1）扫描整个数据集，得到所有出现过的数据，作为候选频繁1项集。k=1，频繁0项集为空集。
    2）挖掘频繁k项集
        a) 扫描数据计算候选频繁k项集的支持度
        b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集
        为空，则直接返回频繁k-1项集的集合作为算法结果，算法结束。如果得到的频繁k项集
        只有一项，则直接返回频繁k项集的集合作为算法结果，算法结束。
        c) 基于频繁k项集，连接生成候选频繁k+1项集。
    3） 令k=k+1，转入步骤2。
算法优缺点

优点：算法思路比较简单，它以递归统计为基础，生成频繁项集，易于实现。Apriori算法作为经典的频繁项目集生成算法，在数据挖掘技术中占有很重要的地位。

缺点：可能产生大量的候选集。因为采用排列组合的方式，把可能的项集都组合出来了；每次计算都需要重新扫描数据集，来计算每个项集的支持度。

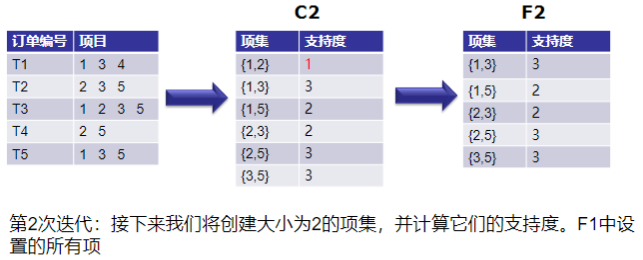
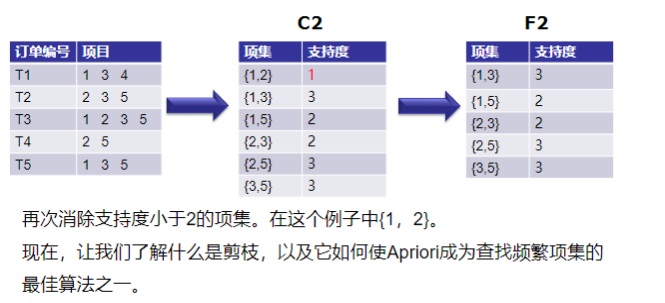
1.3，算法案例

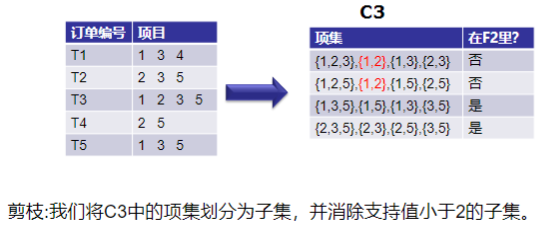
1.4，剪枝操作

2，FP-Growth算法

2.1，算法概述

FP-growth(频繁模式增长)算法是韩家炜老师在2000年提出的关联分析算法，它采取如下分治策略：将提供频繁项集的数据库压缩到一棵频繁模式树（FP-Tree），但仍保留项集关联信息。

该算法是对Apriori方法的改进。生成一个频繁模式而不需要生成候选模式。FP-growth与Apriori算法不同：第一，不产生候选集。第二，只需要两次遍历数据库，大大提高了效率。（第一次是统计每个商品的频次，用于剔除不满足最低支持度的商品，然后排序得到FreqItems。第二次，扫描数据库构建FP树）

FP-growth算法以树的形式表示数据库，称为频繁模式树或FP-tree。此树结构将保持项集之间的关联。数据库使用一个频繁项进行分段。这个片段被称为“模式片段”。分析了这些碎片模式的项集。因此，该方法相对减少了频繁项集的搜索。

FP树(FP-Tree)是由数据库的初始项集组成的树状结构。 FP树的目的是挖掘最频繁的模式。FP树的每个节点表示项集的一个项。根节点表示null，而较低的节点表示项集。在形成树的同时，保持节点与较低节点（即项集与其他项集）的关联。

2.2，算法步骤

频繁模式增长方法可以在不产生候选集的情况下找到频繁模式。

算法步骤

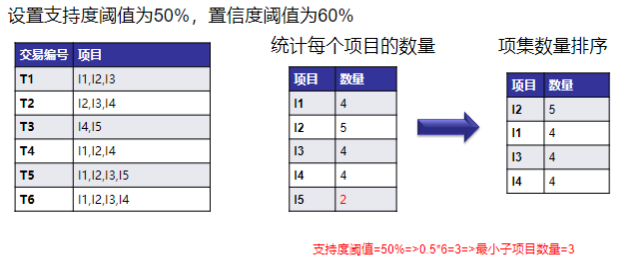
扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。

扫描数据，将读到的原始数据（每条事务）剔除非频繁1项集，并按照支持度降序排列。

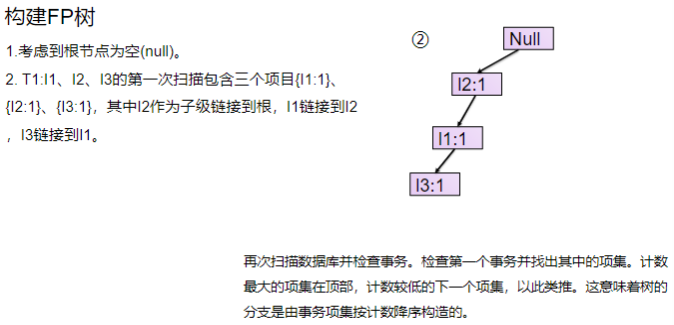
读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。

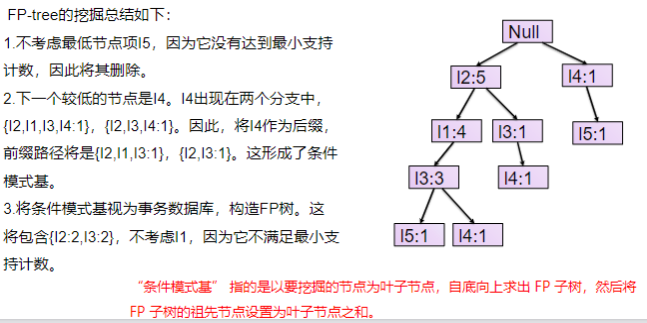
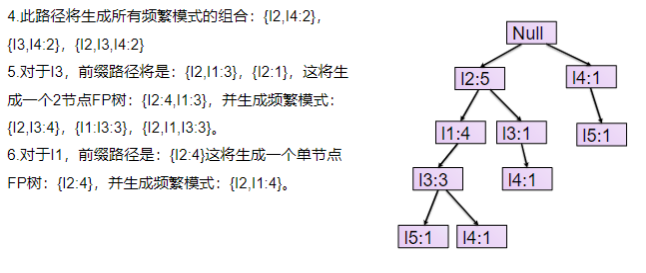
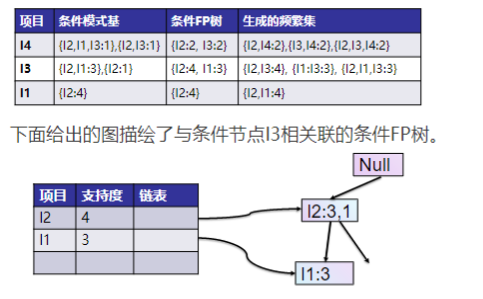
从项目表的底部项依次向上找到项头表项对应的条件模式基。从条件模式基递归挖掘得到项头表项项的频繁项集。

如果不限制频繁项集的项数，则返回步骤4所有的频繁项集，否则只返回满足项数要求的频繁项集。

2.3，算法优缺点

优点：

一个大数据库能够被有效地压缩成比原数据库小很多的高密度结构，避免了重复扫描数据库的开销

该算法基于FP-Tree的挖掘采取模式增长的递归策略，创造性地提出了无候选项目集的挖掘方法，在进行长频繁项集的挖掘时效率较好。

挖掘过程中采取了分治策略，将这种压缩后的数据库DB分成一组条件数据库Dn，每个条件数据库关联一个频繁项，并分别挖掘每一个条件数据库。而这些条件数据库Dn要远远小于数据库DB。

数据库存储在内存中的压缩版本中。

缺点：

该算法采取增长模式的递归策略，虽然避免了候选项目集的产生。但在挖掘过程，如果一项大项集的数量很多，并且由原数据库得到的FP-Tree的分枝很多，而且分枝长度又很长时，该算法需要构造出数量巨大的conditional FP-Tree，不仅费时而且要占用大量的空间，挖掘效率不好，而且采用递归算法本身效率也较低。

由于海量的事物集合存放在大型数据库中，经典的FP-Growth算法在生成新的FP-Tree时每次都要遍历调减模式基两次，导致系统需要反复申请本地以及数据库服务器的资源查询相同内容的海量数据，一方面降低了算法的效率，另一方面给数据库服务器产生高负荷，不利于数据库服务器正常运作。

当数据库较大时，算法可能不适合共享内存。

3，线性回归

3.1，概念

线性回归：是一种通过属性的线性组合来进行预测的线性模型，其目的是找到一条直线或者一个平面或者更高维的超平面，使得预测值与真实值之间的误差最小化。回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

特点：

建模速度快，不需要很复杂的计算，在数据量大的情况下依然运行速度很快。

可以根据系数给出每个变量的理解和解释。

对异常值很敏感。
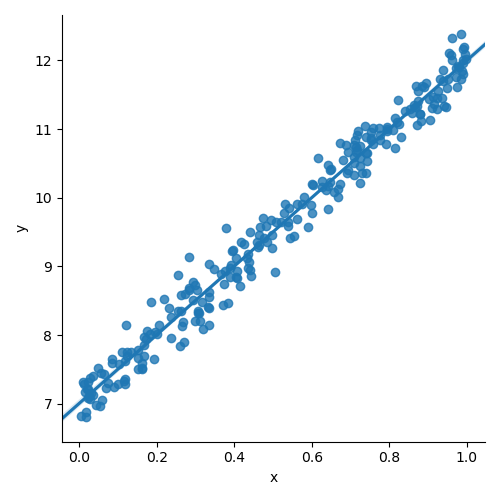
from torch.nn import Linear, Module, MSELoss
from torch.optim import SGD
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
x = np.random.rand(256)
noise = np.random.randn(256) / 4
y = x * 5 + 7 + noise
df = pd.DataFrame()
df['x'] = x
df['y'] = y
sns.lmplot(x='x', y='y', data=df);
plt.show()
假设有训练数据集数为 $m$ 个，特征的数量为 $n$ 个， $(x^{(i)},y^{(i)}),i=1,2,...,m$ 为一个训练数据，其中 $x^{(i)}=(1,x_1^{(i)},x_2^{(i)},...,x_n^{(i)})$ 和 $y^{(i)}$ 分别是第 $i$ 个训练数据对应的自变量与因变量，则回归函数如下：

$h(x)=w_0x^{(0)}_i+w_1x^{(1)}_i+...+w_nx^{(n)}_i=w_0+w_1x^{(1)}_i+...+w_nx^{(n)}_i=W^Tx_i$

其中 $W=[w_0,w_1,...,w_n]^T$ ， $x_i=[x_i^{(0)},x_i^{(1)},...,x_i^{(n)}]^T$

损失函数采用均方误差： $J(w)=\frac{1}{2m}\sum_{i=0}^{m}[h(x^{(i)})-y^{(i)}]^2$ ，其中 $\frac{1}{2}$  的作用在于求导时，消掉常数系数。梯度下降法、最小二乘法等便是求代价函数最小值的方法。

3.2，最小二乘法（LSM）

最小二乘法是比较直接使用矩阵运算来取得 $W$  的一种算法，算法步骤是对代价函数 $J(w)$  求偏导并令其等于 0 ，所得到的 $W$  即为模型参数，即 $min\frac{1}{2m}\sum_{i=0}^{m}[h(x^{(i)})-y^{(i)}]^2$ 。

$J(w)=\frac{1}{2m}\sum_{i=1}^{m}[h(x^{(i)})-y^{(i)}]^2=\frac{1}{2m}(W^TX-Y)^2$

其中 $Y=[y_0,y_1,...,y_m]^T$ ， $X=[x_0,x_1,...,x_m]=\begin{bmatrix} x_0^{(0)} & ... &x_m^{(0)} \\ x_0^{(1)} & ... &x_m^{(1)} \\ ...& ... &... \\ x_0^{(n)} & ... & x_m^{(n)} \end{bmatrix}=\begin{bmatrix} 1 & ... &1 \\ x_0^{(1)} & ... &x_m^{(1)} \\ ...& ... &... \\ x_0^{(n)} & ... & x_m^{(n)} \end{bmatrix}$

对 $W$  求偏导等于0， $\frac{\partial J(w)}{\partial W^T}=\frac{1}{2m}\frac{\partial }{\partial W^T}[(Y-WX)(Y^T-X^TW^T)]$ 

$=\frac{1}{2m}\frac{\partial }{\partial W^T}[YY^T-WXY^T-YX^TW^T+WXX^TW^T]$

$=\frac{1}{2m}[\frac{\partial }{\partial W^T}YY^T-\frac{\partial }{\partial W^T}WXY^T-\frac{\partial }{\partial W^T}YX^TW^T+\frac{\partial }{\partial W^T}WXX^TW^T]$

矩阵分析：矩阵序列，矩阵级数，矩阵函数，微积分，函数应用_燕双嘤-CSDN博客1，矩阵序列1.1，矩阵序列设中的矩阵序列，其中。若：则称矩阵序列收敛于，或称为矩阵序列的极限，记为：或（1）不收敛的矩阵序列称为发散。（2）矩阵序列收敛的本质是矩阵的所有元素都收敛。（3）上一个矩阵序列的收敛相当于个数列同时收敛。（4）用初等分析法太繁琐。（5）与向量序列一样，可以利用矩阵范数来研究矩阵序列的收敛问题。设，则：其中是上的任一矩阵范数。证明：当矩阵序列收敛时，矩阵序列的任意范数也收敛，反之不成...https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11https://blog.csdn.net/qq_42192693/article/details/122251621?spm=1001.2014.3001.5501#t11

$\frac{dX^TX}{dX}=2X$

$\frac{dAX}{dX}=A^T$

$\frac{dX^TAX}{dX}=(A+A^T)X=2AX$ （A为对阵矩阵）

其中第一项与 $W$  无关， $\frac{\partial }{\partial W^T}WXY^T=\frac{\partial }{\partial W^T}YX^TW^T=XY^T$ 

$=\frac{1}{2m}[0-XY^T-XY^T+2XX^TW^T]$

$=\frac{1}{m}[XX^TW^T-XY^T]=0$

$\Rightarrow XX^TW^T=XY^T$

$XX^T$  可逆，要求X是列满秩的，而且求矩阵的逆比较慢。

$\Rightarrow W^T=(XX^T)^{-1}XY^T$

3.3，梯度下降

机器学习：梯度下降_燕双嘤-CSDN博客_机器学习梯度下降1，概述1.1，梯度下降法假定给定函数：，求解该函数的极小值时，k的取值是多少？通常做法：对求导，然后令导数=0，求解 k 值即为所求：1.2，迭代与梯度下降求解求导解法在复杂实际问题中很难计算。迭代法通过从一个初始估计出发寻找一系列近似解来解决优化问题。其基本形式如下：其中被称为学习效率。假设初始化，为了通过迭代让趋近最优解2，要满足两个条件：要能使向最优解逼近。当达到最优解时，要等于0。当达到最优解的时候，要等于...https://shao12138.blog.csdn.net/article/details/121306952https://shao12138.blog.csdn.net/article/details/121306952https://shao12138.blog.csdn.net/article/details/121306952https://shao12138.blog.csdn.net/article/details/121306952https://shao12138.blog.csdn.net/article/details/121306952https://shao12138.blog.csdn.net/article/details/121306952https://shao12138.blog.csdn.net/article/details/121306952https://shao12138.blog.csdn.net/article/details/121306952批量梯度下降：梯度下降的每一步中，都用到了所有的训练样本。

$w_j=w_j-\alpha \frac{1}{m}\sum_{i=1}^{m}[(h(x^{(i)})-y^{(i)})x_j^{(i)}]$

随机梯度下降：梯度下降的每一步中，用到一个样本，在每一次计算之后便更新参数，而不需要首先将所有的训练集求和。

$w=w-\alpha \frac{\partial J(w)}{\partial w},h(x)=W^TX=w_0x_0+w_1x_1+w_2x_2+...+w_nx_n$

$J(w)=\frac{1}{2m}[h(x^{(i)})-y^{(i)}]^2$

$\frac{\partial }{\partial w_j}J(w)=\frac{\partial }{\partial w_j}\frac{1}{2m}[h(x^{(i)})-y^{(i)}]^2=\frac{1}{2m}\frac{\partial }{\partial w_j}[h(x^{(i)})-y^{(i)}]^2$

$=2\frac{1}{2m}[h(x^{(i)})-y^{(i)}]\frac{\partial }{\partial w_j}[h(x^{(i)})-y^{(i)}]$

$=\frac{1}{m}[h(x^{(i)})-y^{(i)}]\frac{\partial }{\partial w_j}[\sum_{i=0}^{n}[w_ix_i^{(i)}-y^{(i)}]]$

$=\frac{1}{m}[h(x^{(i)})-y^{(i)}]x_j^{(i)}$

参数更新： $w_j=w_j-\frac{1}{m}\alpha [h(x^{(i)})-y^{(i)}]x_j^{(i)}$

小批量梯度下降：梯度下降的每一步中，用到了一定批量的训练样本。

$w_j=w_j-\alpha \frac{1}{b}\sum_{k=i}^{i+b-1}[(h(x^{(k)})-y^{(k)})x_j^{(k)}]$

$b=1$ ，随机梯度下降，SGD。

$b=m$ ，批量梯度下降，BSD。

$b=batch\_size$ ，通常为2的倍数，小批量梯度下降，MBGD。

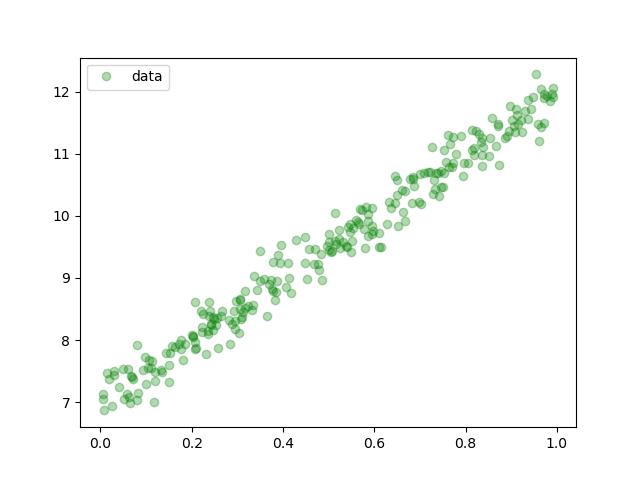
随机生成了一些点，下面将使用PyTorch建立一个线性的模型来对其进行拟合，这就是所说的训练的过程，由于只有一层线性模型，所以就直接使用了。

import torch
from torch.nn import Linear, Module, MSELoss
from torch.optim import SGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#使用随机数来拟合直线
x = np.random.rand(256)
noise = np.random.randn(256) / 4
y = x * 5 + 7 + noise
df = pd.DataFrame()
df['x'] = x
df['y'] = y
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')
#模型
model=Linear(1, 1)
#损失函数
criterion = MSELoss()
#优化器，随机梯度下降
optim = SGD(model.parameters(), lr = 0.01)
#迭代次数
epochs = 3000
for i in range(epochs):
    # 整理输入和输出的数据，这里输入和输出一定要是torch的Tensor类型
    inputs = torch.from_numpy(x_train)
    labels = torch.from_numpy(y_train)
    #使用模型进行预测
    outputs = model(inputs)
    #梯度置0，否则会累加
    optim.zero_grad()
    # 计算损失
    loss = criterion(outputs, labels)
    # 反向传播
    loss.backward()
    # 使用优化器默认方法优化
    optim.step()
    if (i%100==0):
        #每 100次打印一下损失函数，看看效果
        print('epoch {}, loss {:1.4f}'.format(i,loss.data.item()))
[w, b] = model.parameters()
print (w.item(),b.item())
predicted = model.forward(torch.from_numpy(x_train)).data.numpy()
plt.plot(x_train, y_train, 'go', label = 'data', alpha = 0.3)
#拟合直接
plt.plot(x_train, predicted, label = 'predicted', alpha = 1)
plt.legend()
plt.show()

3.4，梯度下降与最小二乘

梯度下降：需要选择学习率 $\alpha$ ，需要多次迭代，当特征数量 $n$  大时也能较好适用，适用于各种类型的模型。

最小二乘法：不需要选择学习率 $\alpha$ ，一次计算得出，需要计算 $(X^TX)^{-1}$ ，如果特征数量 $n$ 较大则运算代价大，因为矩阵逆的计算时间复杂度为 $O(n^3)$ ，通常来说当 $n$ 小于10000 时还是可以接受的，只适用于线性模型，不适合逻辑回归模型等其他模型。

3.5，其他线性回归模型

在机器学习中，有时为了防止模型太复杂容易过拟合，通常会在模型上加入正则项，抑制模型复杂度，防止过拟合。在线性回归中有两种常用的正则，一个是L1正则，一个是L2正则，加入L1正则的称为Lasso回归，加入L2正则的成为Ridge回归也叫岭回归。

Lasso回归： $J(w)=\frac{1}{2m}\sum_{i=0}^{m}[h(x^{(i)})-y^{(i)}]^2+\lambda \sum_{j=1}^{n}|w_j|$ 

岭回归： $J(w)=\frac{1}{2m}\sum_{i=0}^{m}[h(x^{(i)})-y^{(i)}]^2+\lambda \sum_{j=1}^{n}w_j^2$ 

4，逻辑回归

4.1，概念

logistic回归是一种广义线性回归，与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 $wx + b$ ，其中 $w$ 和 $b$ 是待求参数，其区别在于他们的因变量不同，多重线性回归直接将 $wx + b$ 作为因变量，即 $y =wx+b$ ，而logistic回归则通过函数 $L$ 将 $wx + b$ 对应一个隐状态 $p$ ， $p =L(wx+b)$ ，然后根据 $p$ 与 $1-p$ 的大小决定因变量的值。如果 $L$ 是logistic函数，就是logistic回归，如果 $L$ 是多项式函数就是多项式回归。

logistic回归主要是进行二分类预测，而Sigmod函数是最常见的logistic函数，因为Sigmod函数的输出的是是对于0~1之间的概率值，当概率大于0.5预测为1，小于0.5预测为0。说的更通俗一点，就是logistic回归会在线性回归后再加一层logistic函数的调用。

sigmoid函数有一个非常好的性质，即当 $x$  趋近于无穷时， $g(x)$  趋近于1，而当 $x$  趋近于负无穷时， $g(x)$  趋近于0，这非常适合于分类概率模型，可以将 $\left ( -\infty ,+\infty \right )$  的结果映射到 $\left ( 0,1 \right )$  之间并作为概率。

它还有个很好的导数性质： $g'(x)=g(x)(1-g(x))$ 。

二分类中，事件发生与不发生的概率之比为： $\small \frac{p}{1-p}$ ，称为事件的发生比。

其中 $\small p$ 为随机事件发生的概率， $\small p$ 的范围为 $\small [0,1 ]$ 。

取对数得到： $\small log\frac{p}{1-p}$ ，而 $\small log\frac{p}{1-p}=w^Tx=z$

进一步： $\small g(z)=p=\frac{1}{1+e^{-w^Tx}}=\frac{1}{1+e^{-z}}$

当 $\small z>0.5$ 为正样本， $\small z<0.5$ 时为负样本。

假设一个二分类模型：

 ${p(y=1|x;w)=h(x)}$

 $p(y=0|w;w)=1-h(x)$

则： $p(y|x;w)=(h(x))^y(1-h(x))^{1-y}$ 

逻辑回归模型的假设： $h(x)=g(w^Tx)=g(z)$ 

其中， $z=w^Tx$ ，逻辑函数公式为：

$g(z)=\frac{1}{1+e^{-z}}\, \, ,\, \, g'(z)=g(z)(1-g(z))$

4.2，函数优化

损失函数（交叉熵损失）： $L(\hat y,y)=-ylog(\hat y)-(1-y)log(1-\hat y)$ 

$\hat y$  表示预测值 $h(x)$ ， $y$  表示真实值。

概率由逻辑回归的公式求解，那么带进去得到极大似然函数：

$L(w)=\prod_{i=1}^{m}P(y^{(i)}|x(i);w)=\prod_{i=1}^{m}[h(x^{(i)})]^{y^{(i)}}[1-h(x^{(i)})]^{1-y^{(i)}}$ 

两边取对数后，连乘变成连加：

$l(w)=logL(w)=\sum_{i=1}^{m}\left [ y^{(i)}log(h(x^{(i)})) +(1-y^{(i)})log(1-h(x^{(i)}))\right ]$ 

代价函数为（损失函数求和）：

$J(w)=-\frac{1}{m}l(w)=-\frac{1}{m}\sum_{i=1}^{m}\left [ y^{(i)}log(h(x^{(i)})) +(1-y^{(i)})log(1-h(x^{(i)}))\right ]$

$J(w)=-\frac{1}{m}l(w)=-\frac{1}{m}\sum_{i=1}^{m}\left [ y^{(i)}log(h(x^{(i)})) +(1-y^{(i)})log(1-h(x^{(i)}))\right ]$

$=-\frac{1}{m}\sum_{i=1}^{m}\left [ y^{(i)}log(\frac{1}{1+e^{-w^Tx^{(i)}}}) +(1-y^{(i)})log(1-\frac{1}{1+e^{-w^Tx^{(i)}}})\right ]$

$=-\frac{1}{m}\sum_{i=1}^{m}\left [ -y^{(i)}log(1+e^{-w^Tx^{(i)}}) +(1-y^{(i)})log(\frac{e^{-w^Tx^{(i)}}}{1+e^{-w^Tx^{(i)}}})\right ]$

$=-\frac{1}{m}\sum_{i=1}^{m}\left [ -y^{(i)}log(1+e^{-w^Tx^{(i)}}) +(1-y^{(i)})log(\frac{1}{e^{w^Tx^{(i)}}+1})\right ]$

$=-\frac{1}{m}\sum_{i=1}^{m}\left [ -y^{(i)}log(1+e^{-w^Tx^{(i)}}) -(1-y^{(i)})log(1+e^{w^Tx^{(i)}})\right ]$

$\frac{\partial }{\partial w_j}J(w)=\frac{\partial }{\partial w_j}\left [ -\frac{1}{m}\sum_{i=1}^{m}\left [ -y^{(i)}log(1+e^{-w^Tx^{(i)}}) -(1-y^{(i)})log(1+e^{w^Tx^{(i)}})\right ] \right ]$

$=-\frac{1}{m}\sum_{i=1}^{m}\left [ -y^{(i)}\frac{\partial }{\partial w_j}\left [ log(1+e^{-w^Tx^{(i)}}) \right ] -(1-y^{(i)})\frac{\partial }{\partial w_j}\left [ log(1+e^{w^Tx^{(i)}}) \right ] \right ]$

$=-\frac{1}{m}\sum_{i=1}^{m}\left [ -y^{(i)}\frac{-x_j^{(i)}e^{-w^Tx^{(i)}}}{1+e^{-w^Tx^{(i)}}} -(1-y^{(i)}) \frac{x_j^{(i)}e^{-w^Tx^{(i)}}}{1+e^{-w^Tx^{(i)}}}\right ]$

$=-\frac{1}{m}\sum_{i=1}^{m}\left [y^{(i)}-h(x^{(i)})\right ]x_j^{(i)}$

$=\frac{1}{m}\sum_{i=1}^{m}\left [h(x^{(i)}-y^{(i)})\right ]x_j^{(i)}$

故， $w$  更新策略： $w_j=w_j-\alpha \frac{\partial J(w)}{\partial w}=w_j-\alpha\frac{1}{m}\sum_{i=1}^{m}\left [h(x^{(i)}-y^{(i)})\right ]x_j^{(i)}$ 

4.3，引入正则化

机器学习：概念_燕双嘤-CSDN博客1，机器学习概述1.1，机器学习概念机器学习即Machine Learning，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。目的是让计算机模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断完善自身的性能。简单来讲，机器学习就是人们通过提供大量的相关数据来训练机器。DataAnalysis：基本概念，环境介绍，环境搭建，大数据问题_燕双嘤-CSDN博客1，概述1.1，数据的性质所谓数据就是描述事物的符号，是对客观事物的性质、状态和相互关系等进行记载的https://shao12138.blog.csdn.net/article/details/120507206#t6https://shao12138.blog.csdn.net/article/details/120507206#t6https://shao12138.blog.csdn.net/article/details/120507206#t6https://shao12138.blog.csdn.net/article/details/120507206#t6https://shao12138.blog.csdn.net/article/details/120507206#t6https://shao12138.blog.csdn.net/article/details/120507206#t6https://shao12138.blog.csdn.net/article/details/120507206#t6https://shao12138.blog.csdn.net/article/details/120507206#t6 $J(w)=-\frac{1}{m}\sum_{i=1}^{m}\left [ y^{(i)}log(h(x^{(i)})) +(1-y^{(i)})log(1-h(x^{(i)}))\right ]+\frac{\lambda }{2m}\sum_{j=1}^{n}w_j^2$

引入正则化项： $\frac{\lambda }{2m}\sum_{j=1}^{n}w_j^2$ ，当 λ 的值开始上升时，降低了方差。

4.4，逻辑回归实现

UCI German Credit是UCI的德国信用数据集，里面有原数据和数值化后的数据。German Credit数据是根据个人的银行贷款信息和申请客户贷款逾期发生情况来预测贷款违约倾向的数据集，数据集包含24个维度的，1000条数据。

data=np.loadtxt("german.data-numeric")
n,l=data.shape
#数据读取完成后我们要对数据做一下归一化的处理
for j in range(l-1):
    meanVal=np.mean(data[:,j])
    stdVal=np.std(data[:,j])
    data[:,j]=(data[:,j]-meanVal)/stdVal
np.random.shuffle(data)    #打乱数据

区分训练集和测试集，由于这里没有验证集，所以我们直接使用测试集的准确度作为评判好坏的标准。

区分规则：900条用于训练，100条作为测试。

german.data-numeric的格式为，前24列为24个维度，最后一个为要打的标签（0，1），所以我们将数据和标签一起区分出来。

train_data=data[:900,:l-1]
train_lab=data[:900,l-1]-1
test_data=data[900:,:l-1]
test_lab=data[900:,l-1]-1

定义模型：

class LR(nn.Module):
    def __init__(self):
        super(LR,self).__init__()
        self.fc=nn.Linear(24,2) # 由于24个维度已经固定了，所以这里写24
    def forward(self,x):
        out=self.fc(x)
        out=torch.sigmoid(out)
        return out
#测试集上的准确率
def test(pred,lab):
    t=pred.max(-1)[1]==lab
    return torch.mean(t.float())
net=LR() 
criterion=nn.CrossEntropyLoss() # 使用CrossEntropyLoss损失
optm=torch.optim.Adam(net.parameters()) # Adam优化
epochs=1000 # 训练1000次
for i in range(epochs):
    # 指定模型为训练模式，计算梯度
    net.train()
    # 输入值都需要转化成torch的Tensor
    x=torch.from_numpy(train_data).float()
    y=torch.from_numpy(train_lab).long()
    y_hat=net(x)
    loss=criterion(y_hat,y) # 计算损失
    optm.zero_grad() # 前一步的损失清零
    loss.backward() # 反向传播
    optm.step() # 优化
    if (i+1)%100 ==0 : # 这里我们每100次输出相关的信息
        # 指定模型为计算模式
        net.eval()
        test_in=torch.from_numpy(test_data).float()
        test_l=torch.from_numpy(test_lab).long()
        test_out=net(test_in)
        # 使用我们的测试函数计算准确率
        accu=test(test_out,test_l)
        print("Epoch:{},Loss:{:.4f},Accuracy：{:.2f}".format(i+1,loss.item(),accu))
===============================================================
Epoch:100,Loss:0.6313,Accuracy：0.76
Epoch:200,Loss:0.6065,Accuracy：0.79
Epoch:300,Loss:0.5909,Accuracy：0.80
Epoch:400,Loss:0.5801,Accuracy：0.81
Epoch:500,Loss:0.5720,Accuracy：0.82
Epoch:600,Loss:0.5657,Accuracy：0.81
Epoch:700,Loss:0.5606,Accuracy：0.81
Epoch:800,Loss:0.5563,Accuracy：0.81
Epoch:900,Loss:0.5527,Accuracy：0.81
Epoch:1000,Loss:0.5496,Accuracy：0.80