“百钱买百鸡”是一个经典的数学趣题，也是一道著名的整数方程问题，该问题导致三元不定方程组，其重要之处在于开创“一问多答”的先例‌，最早见于《张丘建算经》（约公元5世纪），这是一部中国古代数学著作，主要讲述了算术和代数问题。该问题是其中一个经典的整数方程问题，后来在《算经十书》（中国古代数学教材）中被广泛传播。本文将详细介绍该问题的背景、数学解法，并提供 Python、Java 和 C++ 三种编程语言的实现代码。

原文出处

《张丘建算经·卷上·杂术》中的原文如下：

今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。凡百钱，买鸡百只，问鸡翁、母、雏几何？

现代汉语翻译：
现在有 100 文钱，要买 100 只鸡。已知：

• 公鸡 5 文钱 1 只
• 母鸡 3 文钱 1 只
• 小鸡 1 文钱可以买 3 只

问：如何合理分配公鸡、母鸡、小鸡的数量，使得花费正好 100 文，且总数正好 100 只？

---

一、问题描述

题目：

用 100 文钱买 100 只鸡，已知：

• 公鸡：5 文钱 1 只
• 母鸡：3 文钱 1 只
• 小鸡：1 文钱买 3 只（即 1 只小鸡 ​ 文钱）

求公鸡、母鸡和小鸡的合理购买方案，使得总花费正好为 100 文，且鸡的总数正好是 100 只。

---

二、数学解法

设：

• x 为公鸡的数量
• y 为母鸡的数量
• z 为小鸡的数量

根据题目条件，可以列出以下两个方程：

1. 总数量方程： x + y + z = 100
2. 总价格方程（注意小鸡的价格）：

为了消去分数，方程两边乘以 3：

然后，我们用数量方程 (1) 代入 (2)：

化简后得到：

解整数方程：
由于 x、y 和 z 必须是非负整数，我们枚举 x 的值，并检查 y 是否为整数，最终求得所有解：

• 若 x = 0，则 4y = 100，y = 25，此时 z = 100 - 0 - 25 = 75（可行）。
• 若 x = 4，则 7(4) + 4y = 100，即 28 + 4y = 100，解得 y = 18，此时 z = 100 - 4 - 18 = 78（可行）。
• 若 x = 8，则 7(8) + 4y = 100，即 56 + 4y = 100，解得 y = 11，此时 z = 100 - 8 - 11 = 81（可行）。
• 若 x = 12，则 (12) + 4y = 100，即 84 + 4y = 100，解得 y = 4，此时 z = 100 - 12 - 4 = 84（可行）。

所以，所有整数解为：

即，百钱买百鸡的可行方案如下：

1. 公鸡 0 只，母鸡 25 只，小鸡 75 只
2. 公鸡 4 只，母鸡 18 只，小鸡 78 只
3. 公鸡 8 只，母鸡 11 只，小鸡 81 只
4. 公鸡 12 只，母鸡 4 只，小鸡 84 只

---

三、编程实现

Python 实现

def hundred_chicken():
    for x in range(0, 101):  # 遍历公鸡数量
        if (100 - 7 * x) % 4 == 0:
            y = (100 - 7 * x) // 4
            z = 100 - x - y  # 计算小鸡数量
            if y >= 0 and z >= 0 and (15 * x + 9 * y + z == 300):
                print("公鸡: %d, 母鸡: %d, 小鸡: %d" % (x, y, z))


if __name__ == '__main__':
    hundred_chicken()

运行结果 

公鸡: 0, 母鸡: 25, 小鸡: 75
公鸡: 4, 母鸡: 18, 小鸡: 78
公鸡: 8, 母鸡: 11, 小鸡: 81
公鸡: 12, 母鸡: 4, 小鸡: 84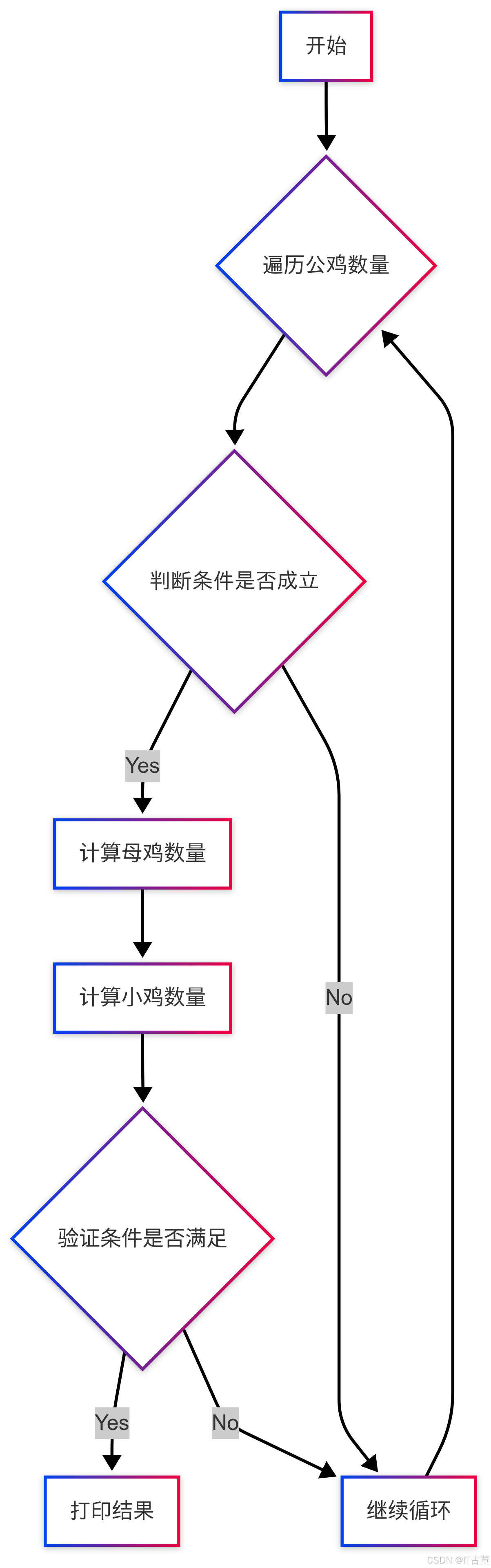

---

Java 实现

public class HundredChicken {
    public static void main(String[] args) {
        for (int x = 0; x <= 100; x++) {
            if ((100 - 7 * x) % 4 == 0) {
                int y = (100 - 7 * x) / 4;
                int z = 100 - x - y;
                if (y >= 0 && z >= 0 && (15 * x + 9 * y + z == 300)) {
                    System.out.println("公鸡: " + x + ", 母鸡: " + y + ", 小鸡: " + z);
                }
            }
        }
    }
}

---

C++ 实现

#include <iostream>
using namespace std;

int main(){
    for (int x = 0; x <= 100; x++){
        if ((100 - 7 * x) % 4 == 0){
            int y = (100 - 7 * x) / 4;
            int z = 100 - x - y;
            if (y >= 0 && z >= 0 && (15 * x + 9 * y + z == 300)) {
                cout << "公鸡: " << x << ", 母鸡: " << y << ", 小鸡: " << z << endl;
            }
        }
    }
    return 0;
}

---

四、总结

数学方法总结：

1. 列方程：用数量和价格方程表示约束条件。
2. 化简方程：消去分数，转化为整数方程 7x + 4y = 100。
3. 穷举法求解：遍历 x 的值，求出所有符合条件的整数解。

代码实现总结：

• Python 代码简洁，使用 range() 遍历 x，检查 y 是否为整数，再计算 z 并验证结果。
• Java 和 C++ 逻辑相同，使用 for 循环遍历 x，同样检查 y 并计算 z。
• 时间复杂度：由于 x 的取值范围是 0 到 100，所以算法复杂度接近 O(100)，即 O(1) 级别，运行速度非常快。

---

通过数学分析和编程求解，我们成功找到了“百钱买百鸡”问题的所有解，并使用 Python、Java 和 C++ 三种语言实现了该问题的自动求解。