NIST SP800-22测试平台源代码Windows系统简化构建方法
在github上下载NIST SP800-22后,直接在linux平台运行较为方便,直接虚拟机里安装linux系统,在文件夹内直接“make”就行。但如果在windows端安装,则有一些麻烦,需要安装一堆零零碎碎的软件。以下采用更简单的方法让windows平台编译源代码。下载链接:通过网盘分享的文件:NIST SP800-22链接: https://pan.baidu.com/s/1BueKoLz
在github上下载NIST SP800-22后,直接在linux平台运行较为方便,直接虚拟机里安装linux系统,在文件夹内直接“make”就行。
但如果在windows端安装,则有一些麻烦,需要安装一堆零零碎碎的软件。
以下采用更简单的方法让windows平台编译源代码。
下载链接:通过网盘分享的文件:NIST SP800-22
链接: https://pan.baidu.com/s/1BueKoLzY4tfpFVyIKfFz3g?pwd=i8v6 提取码: i8v6
1. 安装Dev C++软件
软件版本:Dev-Cpp 5.11 TDM-GCC 4.9.2.exe
1、双击安装。
2、选择语言为英文。
3、点击“I Agree”。
4、直接点击“Next >”。
5、选择安装位置后点击“Install”。
6、安装完成后,打开软件。
2. 解压NIST SP800-22文件夹
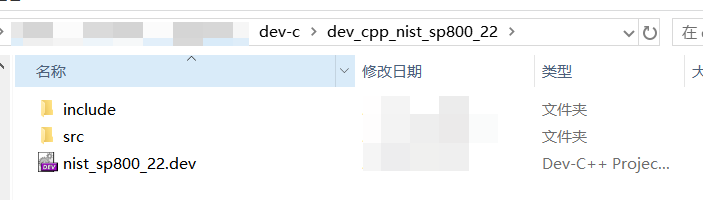
在sts文件夹下,include文件夹内为.h文件,src文件夹内为.c文件,Dev C++需要导入这两个文件夹内的c语言源文件。
3. 构建项目
1、点击“文件->新建->项目”。
2、选择Basic->Empty Project,C项目,修改名称后点击确定。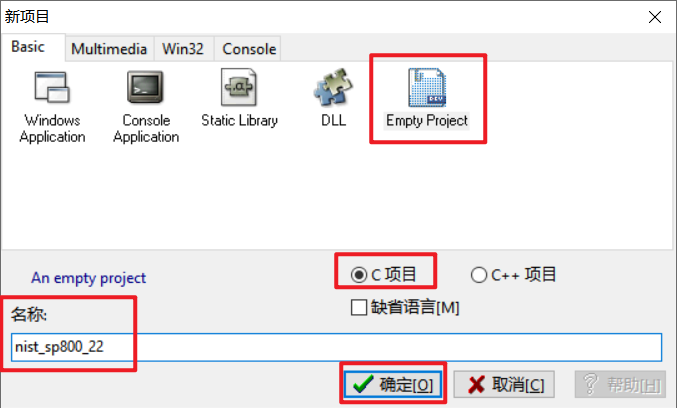
3、选择保存路径。
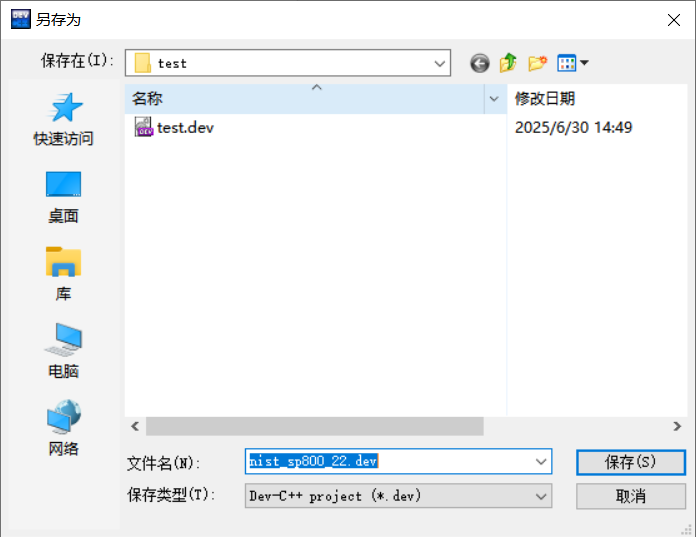
4、复制“sts”文件夹下的“/include”和“/src”文件夹到本地文件夹下。
5、右键点击项目管理的顶层文件目录,“添加”源文件。
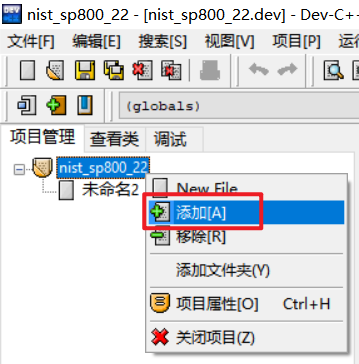
6、把“/include”和“/src”文件夹中的.c和.h文件都加入项目内。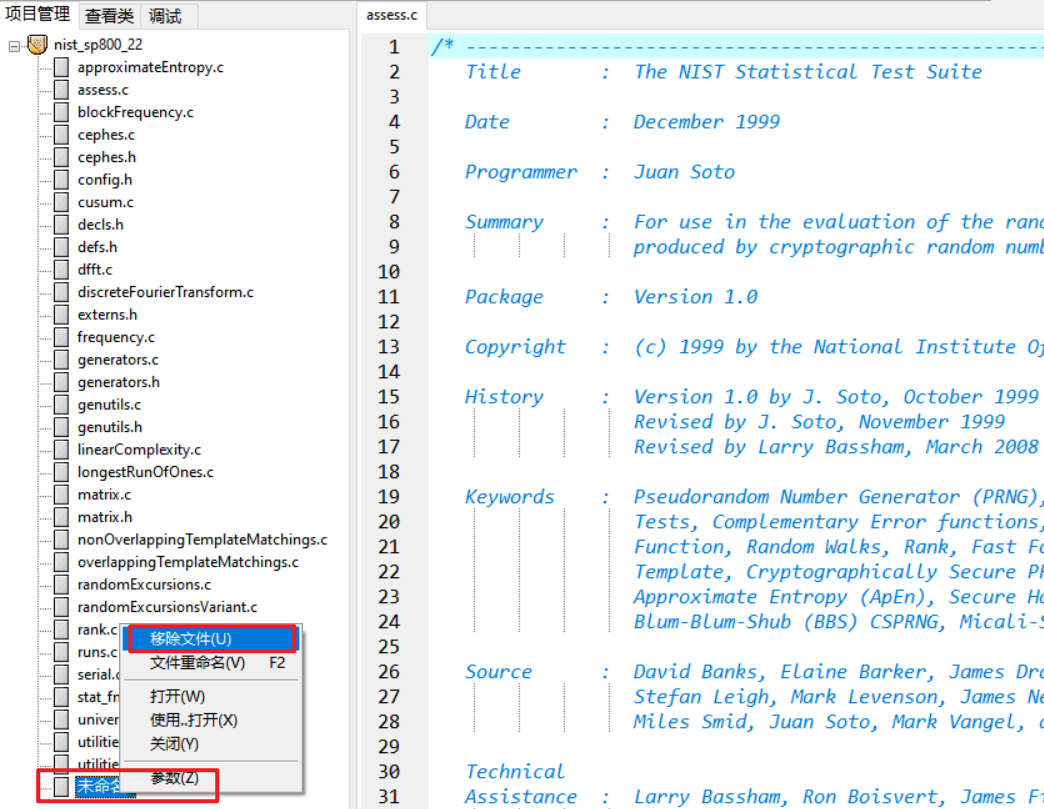
右键自动生产的未命名文件,移除文件。
7、access.c为顶层文件,其中有main函数。
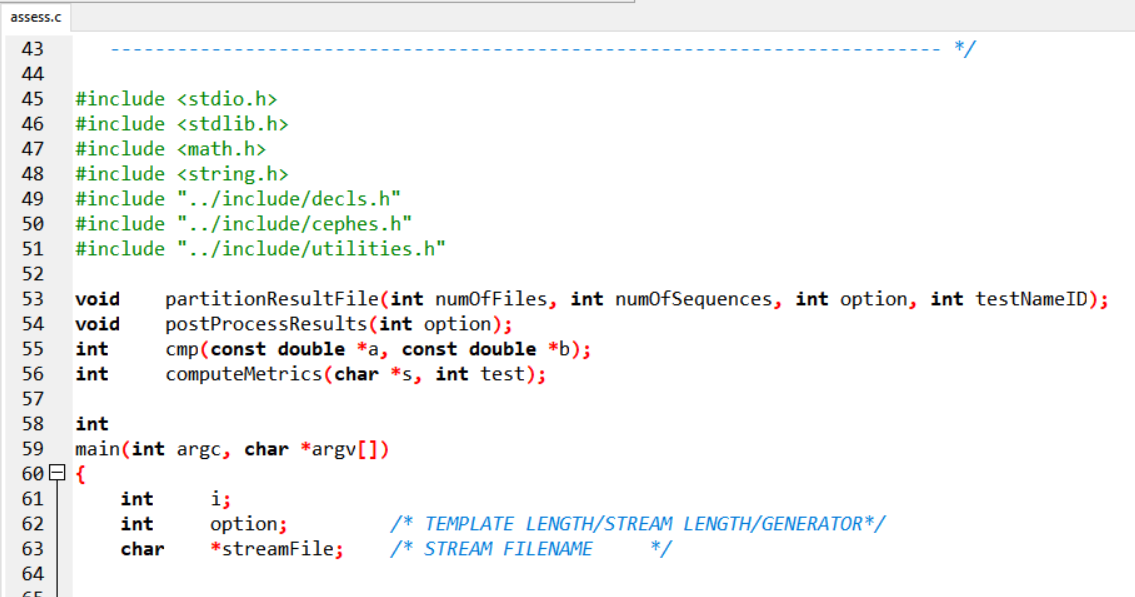
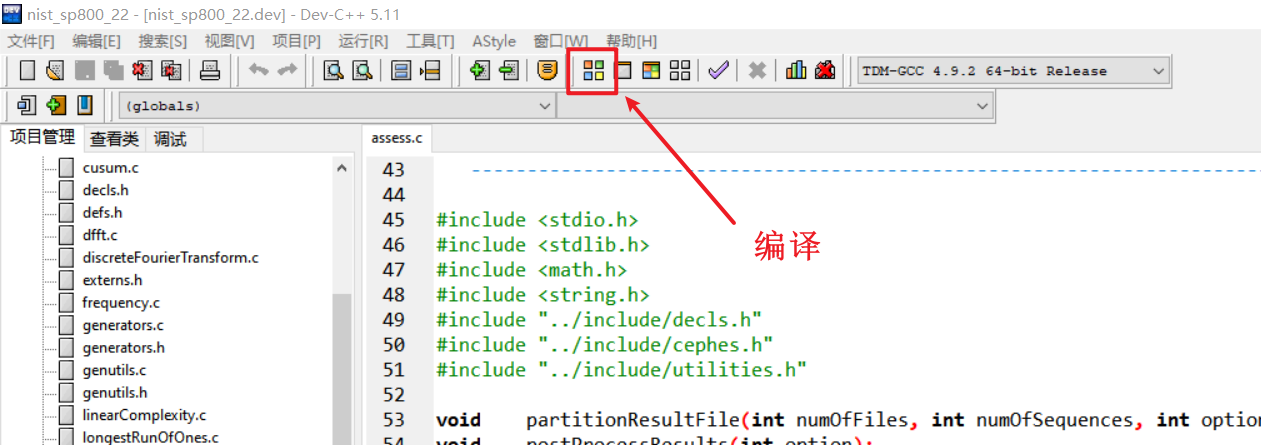
8、点击编译,等待一段时间自动生成makefile和编译。
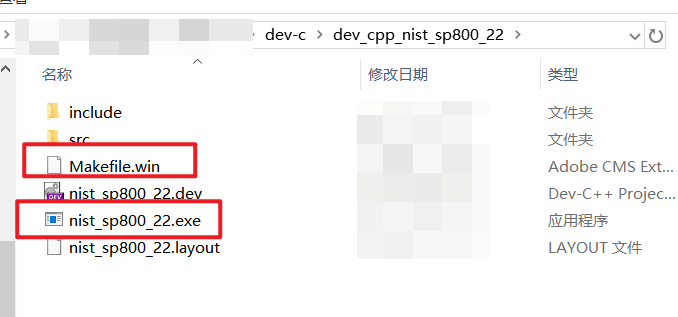
9、查看文件夹内,可以看到“Makefile.win”和“nist_sp800_22.exe”可执行文件。
4. 运行程序
1、复制/sts/data中的测试数据到dev中exe的文件夹下。
2、在.exe所在的文件夹下创建createFolder.bat,以创建实验文件夹experiments和其内部文件夹。createFolder.bat内部代码如下:
setlocal enabledelayedexpansion
set folders=AlgorithmTesting BBS CCG G-SHA1 LCG MODEXP MS QCG1 QCG2 XOR
for %%d in (%folders%) do (
mkdir "experiments\%%d\Frequency"
mkdir "experiments\%%d\BlockFrequency"
mkdir "experiments\%%d\Runs"
mkdir "experiments\%%d\LongestRun"
mkdir "experiments\%%d\Rank"
mkdir "experiments\%%d\FFT"
mkdir "experiments\%%d\NonOverlappingTemplate"
mkdir "experiments\%%d\OverlappingTemplate"
mkdir "experiments\%%d\Universal"
mkdir "experiments\%%d\LinearComplexity"
mkdir "experiments\%%d\Serial"
mkdir "experiments\%%d\ApproximateEntropy"
mkdir "experiments\%%d\CumulativeSums"
mkdir "experiments\%%d\RandomExcursions"
mkdir "experiments\%%d\RandomExcursionsVariant"
)
endlocal
所有新添加的文件如下:
3、在路径处输入cmd,打开终端。
4、双击createFolder.bat即可生成文件夹。
5、输入nist_sp800_22.exe 100000,即可打开测试程序。
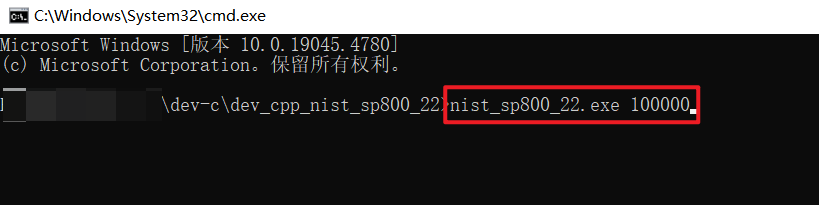
6、以下步骤可以查看源文件中的“README.md”。
部分操作如下:
G E N E R A T O R S E L E C T I O N
______________________________________
[0] Input File [1] Linear Congruential
[2] Quadratic Congruential I [3] Quadratic Congruential II
[4] Cubic Congruential [5] XOR
[6] Modular Exponentiation [7] Blum-Blum-Shub
[8] Micali-Schnorr [9] G Using SHA-1
Enter Choice: 0
User Prescribed Input File: data/data.pi
S T A T I S T I C A L T E S T S
_________________________________
[01] Frequency [02] Block Frequency
[03] Cumulative Sums [04] Runs
[05] Longest Run of Ones [06] Rank
[07] Discrete Fourier Transform [08] Nonperiodic Template Matchings
[09] Overlapping Template Matchings [10] Universal Statistical
[11] Approximate Entropy [12] Random Excursions
[13] Random Excursions Variant [14] Serial
[15] Linear Complexity
INSTRUCTIONS
Enter 0 if you DO NOT want to apply all of the
statistical tests to each sequence and 1 if you DO.
Enter Choice: 1
P a r a m e t e r A d j u s t m e n t s
-----------------------------------------
[1] Block Frequency Test - block length(M): 128
[2] NonOverlapping Template Test - block length(m): 9
[3] Overlapping Template Test - block length(m): 9
[4] Approximate Entropy Test - block length(m): 10
[5] Serial Test - block length(m): 16
[6] Linear Complexity Test - block length(M): 500
Select Test (0 to continue): 0
How many bitstreams? 10
Input File Format:
[0] ASCII - A sequence of ASCII 0's and 1's
[1] Binary - Each byte in data file contains 8 bits of data
Select input mode: 0
Statistical Testing In Progress.........
Statistical Testing Complete!!!!!!!!!!!!
7、在experiments/AlgorithmTesting中查看finalAnalysisReport.txt。
8、测试结果如下:
------------------------------------------------------------------------------
RESULTS FOR THE UNIFORMITY OF P-VALUES AND THE PROPORTION OF PASSING SEQUENCES
------------------------------------------------------------------------------
generator is <data/data.pi>
------------------------------------------------------------------------------
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST
------------------------------------------------------------------------------
1 1 3 0 0 2 1 0 1 1 0.534146 10/10 Frequency
1 2 1 0 2 2 1 0 1 0 0.739918 10/10 BlockFrequency
1 1 1 2 1 0 0 2 1 1 0.911413 10/10 CumulativeSums
1 2 0 1 1 1 1 2 1 0 0.911413 10/10 CumulativeSums
0 4 1 1 0 2 0 1 0 1 0.122325 10/10 Runs
0 1 0 4 1 0 1 1 1 1 0.213309 10/10 LongestRun
1 1 0 1 1 1 2 1 0 2 0.911413 10/10 Rank
2 1 0 0 2 1 1 1 2 0 0.739918 10/10 FFT
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
0 0 0 0 0 0 0 0 10 0 0.000000 * 10/10 NonOverlappingTemplate
4 0 1 2 0 1 0 0 0 2 0.066882 9/10 OverlappingTemplate
10 0 0 0 0 0 0 0 0 0 0.000000 * 0/10 * Universal
0 1 1 2 0 1 3 1 1 0 0.534146 10/10 ApproximateEntropy
0 2 0 0 0 0 0 0 0 0 ---- 2/2 RandomExcursions
0 0 0 0 1 0 1 0 0 0 ---- 2/2 RandomExcursions
0 0 0 0 1 0 0 1 0 0 ---- 2/2 RandomExcursions
0 0 0 0 0 0 1 1 0 0 ---- 2/2 RandomExcursions
0 0 1 0 0 0 0 1 0 0 ---- 2/2 RandomExcursions
0 0 1 0 0 0 0 0 0 1 ---- 2/2 RandomExcursions
0 0 0 1 0 0 1 0 0 0 ---- 2/2 RandomExcursions
0 1 0 0 1 0 0 0 0 0 ---- 2/2 RandomExcursions
0 0 0 1 0 0 0 1 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 1 0 0 0 1 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 1 0 0 0 0 0 1 ---- 2/2 RandomExcursionsVariant
0 0 0 1 0 1 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 0 1 1 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 0 2 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 1 1 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 0 0 1 1 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 0 0 0 2 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 0 0 0 0 0 0 0 1 ---- 2/2 RandomExcursionsVariant
0 1 0 0 0 0 0 0 1 0 ---- 2/2 RandomExcursionsVariant
0 1 0 1 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 1 0 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 0 1 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 2 0 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 1 1 0 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 0 1 0 1 0 0 0 0 0 ---- 2/2 RandomExcursionsVariant
0 1 0 0 0 0 1 0 0 0 ---- 2/2 RandomExcursionsVariant
3 0 2 1 0 0 1 0 1 2 0.350485 9/10 Serial
2 2 1 1 0 2 0 0 0 2 0.534146 9/10 Serial
2 2 1 0 0 1 1 0 2 1 0.739918 10/10 LinearComplexity
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The minimum pass rate for each statistical test with the exception of the
random excursion (variant) test is approximately = 8 for a
sample size = 10 binary sequences.
The minimum pass rate for the random excursion (variant) test
is approximately = 1 for a sample size = 2 binary sequences.
For further guidelines construct a probability table using the MAPLE program
provided in the addendum section of the documentation.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容









所有评论(0)