数字IC前端学习笔记：优化的基4布斯编码华莱士树乘法器

在Design Compiler中使用report_area命令，报告所设计电路的面积占用情况，如图4所示，设计使用的面积也低于普通的基4布斯华莱士树编码乘法器器，从RTL代码中也可以看到这一点，上节的乘法器使用了22个全加器和5个半加器，而优化后只使用了14个全加器和8个半加器，使用的资源大大减少。前文提到的基4布斯编码华莱士树乘法器的一部分的电路面积是由补位逻辑所带来的——为了保证求和正确，所

日晨难再

1055人浏览 · 2023-11-01 00:03:45

日晨难再 · 2023-11-01 00:03:45 发布

本文是对前文设计的乘法器，即基4布斯编码华莱士树乘法器的补充和优化，具体关于基4布斯编码和华莱士树的内容可以从以往的文章中获得。

数字IC前端学习笔记：数字乘法器的优化设计（基4布斯编码华莱士树乘法器）https://blog.csdn.net/weixin_45791458/article/details/134145641和
数字IC前端学习笔记：数字乘法器的优化设计(Wallace Tree乘法器）https://blog.csdn.net/weixin_45791458/article/details/133611299

前文提到的基4布斯编码华莱士树乘法器的一部分的电路面积是由补位逻辑所带来的——为了保证求和正确，所有的部分积都会需要被符号拓展至乘积结果的位宽以保证在最差情况下都不会溢出。这对于位宽较大的乘法器而言是一笔不小的面积开销，如表1的八位数相乘产生的部分积左侧的S就是因为要补位至十六位所引入的。

表1 补位逻辑

可以发现，这种符号拓展要么全是0要么全是1，根据这点特性可以对它进行简化，首先考虑所有部分积都为负的情况，部分积的符号位拓展后的分布如表2所示。

表2 负部分积的累加

如果其中某个部分积为正，那么就需要将符号位都变为0，这只需要在这些拓展的全为1的符号位的最低位再加上1即可表示正确的符号位，即全为0。换句话说，只需要在拓展符号位的最低位加上取反的符号位，如表3所示。将所有的符号位中的1相加，可以得到如表4形式的部分积。

表3 符号位修正

表4 等效补位逻辑

可以将第一行的1与第一个部分积合并，即合并为!SSS的形式，总结出规律，所有部分积对符号位取反，并在高位补一个1，最后在第一个部分积的符号位加一个1即可完成补位逻辑的优化。注意，这里的部分积（包括符号位）为九位，因为基4布斯编码可能会出现乘2的操作，当编码没有乘2操作时，设计也需要将部分积符号拓展至9位再进行等效的转换。

具体的Verilog代码实现见附录，Modelsim软件仿真截图如图1所示。使用Synopsis的综合工具Design Compiler综合的结果如图2所示，综合使用了0.13μm工艺库。

图1 优化的基4布斯编码华莱士树乘法器仿真结果

图2 优化的基4布斯编码华莱士树乘法器综合结果

在Design Compiler中使用report_timing命令，可以得到关键路径的延迟，如图3所示，可以看到，改良后的逻辑延迟相比于改良前有较大的降低，这是由于部分积数量的减少和补位逻辑的简化共同决定的。

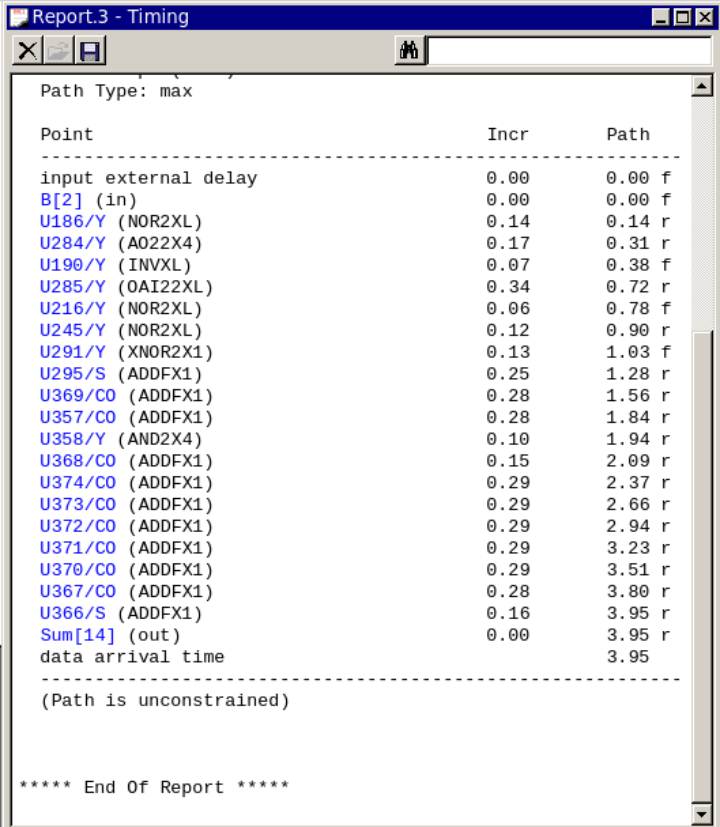
图3 优化的基4布斯编码华莱士树乘法器关键路径报告

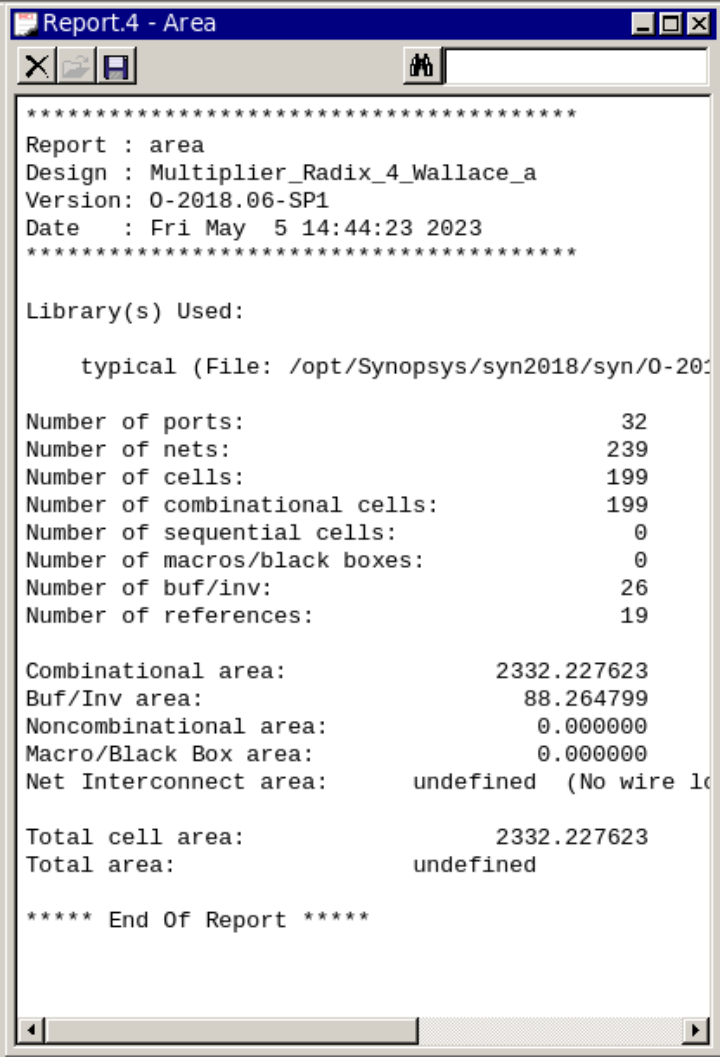
图4 优化的基4布斯编码华莱士树乘法器面积报告

优化的基4布斯编码华莱士树乘法器的Verilog代码如下所示。

// 布斯编码器
module Booth_Encoder(
    input    [2:0]    Code,
    output            Neg,
    output            Zero,
    output            One,
    output            Two
);
 
    assign Neg = Code[2];
    assign Zero = (Code == 3'b000) || (Code == 3'b111);
    assign Two = (Code == 3'b100) || (Code == 3'b011);
    assign One = (!Zero) & (!Two);
 
endmodule

module Partial_Generater(
    input    [7:0]    Multiplicand,
    input             Neg,
    input             Zero,
    input             One,
    input             Two,
    output   [9:0]    Partial_Product
);

    reg [8:0]Partial_Product_t;

    always@(*) begin
        if(Zero) Partial_Product_t = 9'b0;
        else if(One)begin
            if(Neg)	Partial_Product_t = ~{Multiplicand[7], Multiplicand}+1'b1;
            else Partial_Product_t = {Multiplicand[7], Multiplicand};
        end
        else if(Two)begin
            if(Neg)	Partial_Product_t = ~{Multiplicand, 1'b0}+1;
            else Partial_Product_t = {Multiplicand, 1'b0};
        end   
    end
    assign Partial_Product = {1'b1,!Partial_Product_t[8], Partial_Product_t[7:0]};

endmodule

// 半加器
module Adder_half(
    input  Add1,
    input  Add2,
    output Res,
    output Carry
);
 
    assign Res = Add1 ^ Add2;
    assign Carry = Add1 & Add2;
 
endmodule
 
// 全加器
module Adder(
    input  Add1,
    input  Add2,
    input  I_carry,
    output Res,
    output Carry
);
 
    assign Res = Add1 ^ Add2 ^ I_carry;
    assign Carry = (Add1 & Add2) | ((Add1 ^ Add2) & I_carry);
 
endmodule

module Multiplier_Radix_4_Wallace_a(
    input      [7:0]    A,
    input      [7:0]    B,
    output     [15:0]   Sum
);
    //A 被乘数
    //B 乘数
    wire Neg [3:0];
    wire Zero [3:0];
    wire One [3:0];
    wire Two [3:0];
    wire [9:0] Partial_Product_t;
    wire [9:0] Partial_Product[3:1];
    wire [10:0] Partial_Product_0;
    wire [9:0] Result_0;
    wire [9:0] Carry_0;
    wire [10:0] Result_1;
    wire [10:0] Carry_1;

    // 布斯编码器
    Booth_Encoder Booth_Encoder_0({B[1:0], 1'b0}, Neg[0], Zero[0], One[0], Two[0]);
    Booth_Encoder Booth_Encoder_1({B[3:1]}, Neg[1], Zero[1], One[1], Two[1]);
    Booth_Encoder Booth_Encoder_2({B[5:3]}, Neg[2], Zero[2], One[2], Two[2]);
    Booth_Encoder Booth_Encoder_3({B[7:5]}, Neg[3], Zero[3], One[3], Two[3]);

    // 部分积生成器
    Partial_Generater Partial_Generater_0(A, Neg[0], Zero[0], One[0], Two[0], Partial_Product_t);
    Partial_Generater Partial_Generater_1(A, Neg[1], Zero[1], One[1], Two[1], Partial_Product[1]);
    Partial_Generater Partial_Generater_2(A, Neg[2], Zero[2], One[2], Two[2], Partial_Product[2]);
    Partial_Generater Partial_Generater_3(A, Neg[3], Zero[3], One[3], Two[3], Partial_Product[3]);

    assign Partial_Product_0 = {Partial_Product_t[8], !Partial_Product_t[8], !Partial_Product_t[8], Partial_Product_t[7:0]};

    // 华莱士树结构
    // 阶段1
    // ********************************************************************************************
    assign Sum[0] = Partial_Product_0[0];
    assign Sum[1] = Partial_Product_0[1];
    assign Sum[2] = Result_0[0];
    Adder_half Adder_half_0(Partial_Product_0[2], Partial_Product[1][0], Result_0[0], Carry_0[0]);
    Adder_half Adder_half_1(Partial_Product_0[3], Partial_Product[1][1], Result_0[1], Carry_0[1]);
    Adder Adder_0(Partial_Product_0[4], Partial_Product[1][2], Partial_Product[2][0], Result_0[2], Carry_0[2]);
    Adder Adder_1(Partial_Product_0[5], Partial_Product[1][3], Partial_Product[2][1], Result_0[3], Carry_0[3]);
    Adder Adder_2(Partial_Product_0[6], Partial_Product[1][4], Partial_Product[2][2], Result_0[4], Carry_0[4]);
    Adder Adder_3(Partial_Product_0[7], Partial_Product[1][5], Partial_Product[2][3], Result_0[5], Carry_0[5]);
    Adder Adder_4(Partial_Product_0[8], Partial_Product[1][6], Partial_Product[2][4], Result_0[6], Carry_0[6]);
    Adder Adder_5(Partial_Product_0[9], Partial_Product[1][7], Partial_Product[2][5], Result_0[7], Carry_0[7]);
    Adder Adder_6(Partial_Product_0[10], Partial_Product[1][8], Partial_Product[2][6], Result_0[8], Carry_0[8]);
    Adder_half Adder_half_3(Partial_Product[1][9], Partial_Product[2][7], Result_0[9], Carry_0[9]);
    // ********************************************************************************************

    // 阶段2
    // ********************************************************************************************
    assign Sum[3] = Result_1[0];
    Adder_half Adder_half_4(Result_0[1], Carry_0[0], Result_1[0], Carry_1[0]);
    Adder_half Adder_half_5(Result_0[2], Carry_0[1], Result_1[1], Carry_1[1]);
    Adder_half Adder_half_6(Result_0[3], Carry_0[2], Result_1[2], Carry_1[2]);
    Adder Adder_7(Result_0[4], Carry_0[3], Partial_Product[3][0], Result_1[3], Carry_1[3]);
    Adder Adder_8(Result_0[5], Carry_0[4], Partial_Product[3][1], Result_1[4], Carry_1[4]);
    Adder Adder_9(Result_0[6], Carry_0[5], Partial_Product[3][2], Result_1[5], Carry_1[5]);
    Adder Adder_10(Result_0[7], Carry_0[6], Partial_Product[3][3], Result_1[6], Carry_1[6]);
    Adder Adder_11(Result_0[8], Carry_0[7], Partial_Product[3][4], Result_1[7], Carry_1[7]);
    Adder Adder_12(Result_0[9], Carry_0[8], Partial_Product[3][5], Result_1[8], Carry_1[8]);
    Adder Adder_13(Partial_Product[2][8], Carry_0[9], Partial_Product[3][6], Result_1[9], Carry_1[9]);
    Adder_half Adder_half_7(Partial_Product[2][9], Partial_Product[3][7], Result_1[10], Carry_1[10]);
    // ********************************************************************************************

    // 向量合并
    // ********************************************************************************************
    assign Sum[15:4] = {1'b0, Partial_Product[3][8], Result_1[10:1]}+{Partial_Product[3][9], Carry_1[10:0]};
    // ********************************************************************************************

endmodule

技术共进，成长同行——讯飞AI开发者社区

更多推荐

论文笔记：AlphaEdit: Null-Space Constrained Knowledge Editing for Language Models（AlphaEdit）

论文发表于人工智能顶会ICLR（基于定位和修改的模型编辑方法（针对和等）会破坏LLM中最初保存的知识，特别是在顺序编辑场景。为此，本文提出AlphaEdit：1、在将保留知识应用于参数之前，将扰动投影到保留知识的零空间上。2、从理论上证明，这种预测确保了在查询保留的知识时，编辑后的LLM的输出保持不变，从而减轻中断问题。3、对各种LLM（包括LLaMA3、GPT2XL和GPT-J）的广泛实验表明，