TOPSIS （Technique for Order Preference by Similarity to an Ideal Solution ）法是C.L.Hwang和K.Yoon于1981年首次提出，TOPSIS法根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价。

        TOPSIS方法是一种基于对数据样本进行排序的方法，旨在通过通过构造一个理想化的目标，来评估各个样本的综合性能，从而选择最佳的方案。具体而言，该方法会根据所提供的数据特征维度，构造一个肯定的理想目标（positive ideal solution）和一个否定的理想目标（negative ideal solution），然后计算每个样本与这两个目标之间的距离。其公式如下：

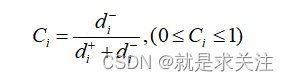
         其中，d-表示负理想值，d+表示正理想值，则表示理想解的贴近度，根据的值按从小到大的顺序对各评价目标进行排列，该值越大，越符合消费者的需求策略。其python的实现代码如下：

import numpy as np

data=np.array([[0.18,	0.37,	0.2,	0.1,	0.37,	0.21],
[0.16,	0.12,	0.13,	0.12,	0.19,	0.025],
[0.14,	0.19,	0.21,	0.20,	0.13,	0.12],
[0.22,	0.18,	0.21,	0.17,	0.16,	0.14],
[0.21,	0.19,	0.20,	0.09,	0.23,	0.18]])  ##方案7


def jisuan(data): #确定最优、最劣理想解分别为maxl,minl
    maxl=[]
    minl=[]
    for i in range(0,2):   ###第
        maxl.append(np.min(data[:,i]))
        minl.append(np.max(data[:,i]))
    for i in range(2,5):
        maxl.append(np.max(data[:,i]))
        minl.append(np.min(data[:,i]))
    # for i in range(5,7):
    #     maxl.append(np.min(data[:,i]))
    #     minl.append(np.max(data[:,i]))
    return maxl,minl


def D(maxl,minl,data): #计算到每个方案到最优、最劣理想解的距离，分别为D_jia,D_jian
    D_jia=[]
    D_jian=[]
    for i in range(0,5):
        a=np.square(data[i,0]-maxl[0])+np.square(data[i,1]-maxl[1])+np.square(data[i,2]-maxl[2])+np.square(data[i,3]-maxl[3])+np.square(data[i,4]-maxl[4])
        a=np.sqrt(a)
        D_jia.append(a)
        b=np.square(data[i,0]-minl[0])+np.square(data[i,1]-minl[1])+np.square(data[i,2]-minl[2])+np.square(data[i,3]-minl[3])+np.square(data[i,4]-minl[4])
        b=np.sqrt(b)
        D_jian.append(b)
    return D_jia,D_jian

def biaozhunhua(data): #标准化处理
    data_biaozhun=np.zeros([5,6])
    print(data_biaozhun)
    for i in range(0,6):     #列
        for j in range(0,5): #行
           data_biaozhun[j,i]=(data[j,i]-np.min(data[:,i]))/(np.max(data[:,i])-np.min(data[:,i]))
    return data_biaozhun

#print(data_600s.dtype)
data_xin=biaozhunhua(data) #先无量纲化
print("标准化后",data_xin)
#print("标准化后",biaozhun_75)
maxl,minl=jisuan(data_xin)##计算最优、最劣理想解
print(maxl)
print(minl)
D_jia,D_jian=D(maxl,minl,data_xin) #计算每个方案到最优、最劣理想解的距离
print('正理想解',D_jia)
print('负理想解',D_jian)
a=0
for i in range(0,7):
    a=a+(D_jian[i]/(D_jian[i]+D_jia[i]))
    print(D_jian[i]/(D_jian[i]+D_jia[i])) ##输出的是最后每个方案综合得分
print('归一化得分为：')
for i in range(0,7):
    print((D_jian[i]/(D_jian[i]+D_jia[i]))/a)##输出的是每个方案综合得分归一化后的数值。

输出结果如下： 

标准化后 [[0.5        1.         0.875      0.09090909 1.         1.        ]
 [0.25       0.         0.         0.27272727 0.25       0.        ]
 [0.         0.28       1.         1.         0.         0.51351351]
 [1.         0.24       1.         0.72727273 0.125      0.62162162]
 [0.875      0.28       0.875      0.         0.41666667 0.83783784]]
[0.0, 0.0, 1.0, 1.0, 1.0]
[1.0, 1.0, 0.0, 0.0, 0.0]
正理想解 [1.4463994195905001, 1.4676258446329946, 1.0384603988597736, 1.3775359034483479, 1.4832153511131745]
负理想解 [1.4226346905688467, 1.3036027636090897, 1.8757398540309367, 1.4567603165362208, 1.2137796798064762]
0.49585840946653414
0.4704060717805681
0.6436550996007623
0.5139760291336635