图的搜索算法

前言

在很多情况下，我们需要遍历图，得到图的一些性质，例如，找出图中与指定的顶点相连的所有顶点，或者判定某个顶点与指定顶点是否相通，是非常常见的需求。本文讲解图的深度优先搜索和广度优先搜索两种搜索的思想以及代码实现。

一、深度优先搜索

1. 搜索思路

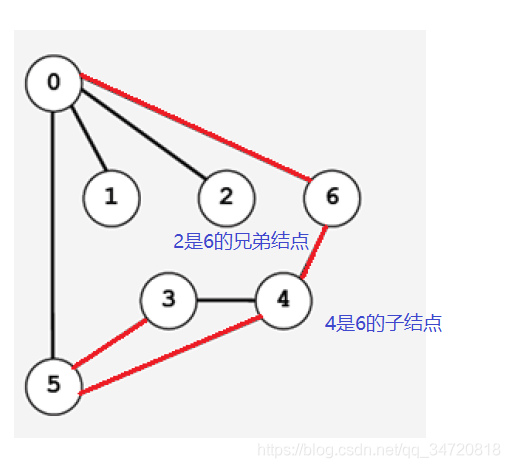
• 在搜索时如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，再找兄弟结点。下图以结点6为例，说明什么是子结点，什么是兄弟结点。
  
• 下图是一个顶点的深度优先搜索顺序
  

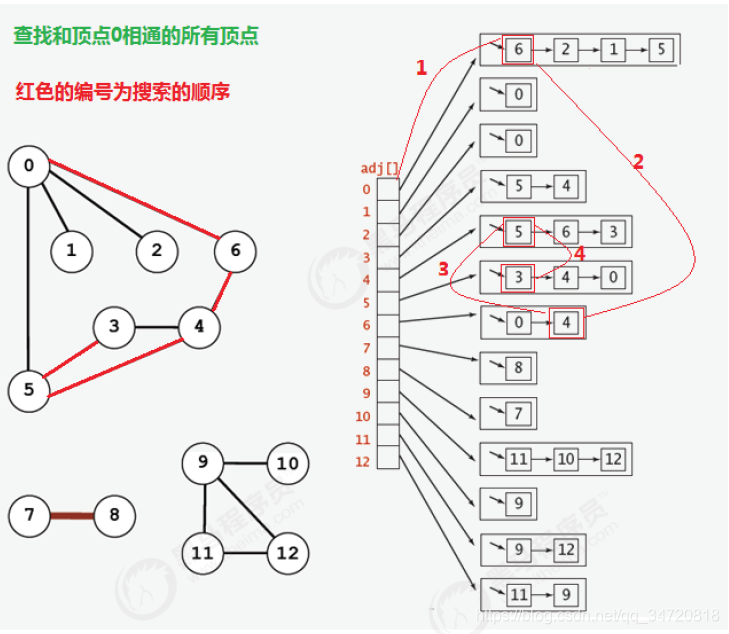
2. 代码实现

public class DepthFirstSearch {
    private boolean[] marked;//索引代表顶点，值表示当前顶点是否已经被搜索
    private int count;//记录有多少个顶点与s顶点相通

    //构造深度优先搜索对象，使用深度优先搜索找出G图中s顶点的所有相通顶点
    public DepthFirstSearch(Graph G,int s)
    {
        //1.初始化代表顶点是否被搜索过的marked数组
        marked=new boolean[G.V()];
        //2.初始化G图中多少个顶点与顶点s相通，初始情况下count为0
        count=0;
        //3.调用深度优先搜索方法，更新count的值和marked的值
        dfs(G,s);
    }
    //使用深度优先搜索找出G图中v顶点的所有相通顶点
    private void dfs(Graph G, int v)
    {
        //1.将当前顶点标记为已搜索
        marked[v]=true;
        //2.搜索当前顶点的邻接表，若邻接表中的顶点不为0，如果邻接表中的顶点未被搜索，这递归深度优先搜索该顶点
        for (Integer w : G.adj(v)) {
            if (!marked[w])
                dfs(G,w);
        }
        //3.每次深度优先搜索后，count+1
        count++;
    }
    //判断w顶点与s顶点是否相通
    public boolean marked(int w)
    {
        //如果相通，则一定被搜索过
        return marked[w];
    }
    //获取与顶点s相通的所有顶点的总数
    public int count()
    {
        return count;
    }

二、广度优先搜索

1. 搜索思路

• 如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，然后找子结点。
• 下图是一个顶点的广度优先搜索顺序
  

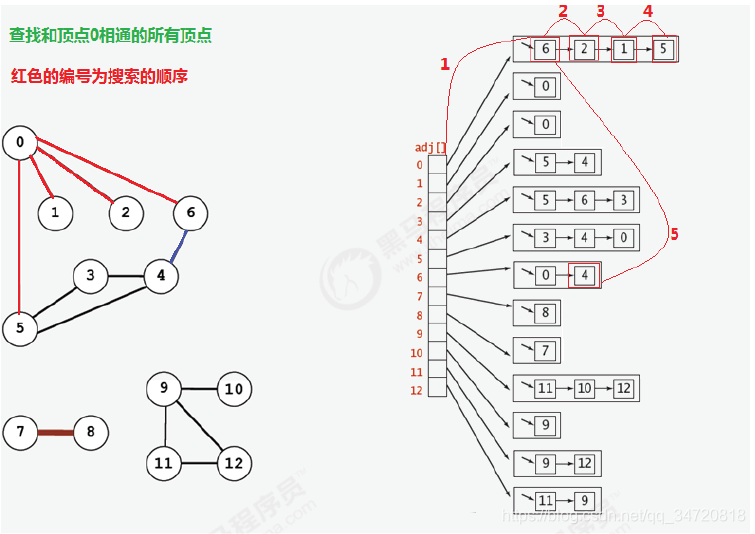
2. 代码实现

public class BreadthFirstSearch {
    private boolean[] marked;//标识顶点是否被搜索过
    private int count;//与顶点相通的所有顶点个数
    private Queue<Integer> waitSearch;//辅助队列，用来存储待搜索的顶点

    //构造广度优先搜索对象，使用广度优先搜索找出G图中s顶点的所有相邻顶点
    public BreadthFirstSearch(Graph G,int s)
    {
        this.marked=new boolean[G.V()];
        this.count=0;
        this.waitSearch=new Queue<Integer>();
        BFS(G,s);
    }

    //广度优先搜索图G中与顶点V相通的所有顶点
    public void BFS(Graph G,int V)
    {
        //1.将顶点V标记为已搜索
        marked[V]=true;
        //2.将顶点V入队
        waitSearch.enqueue(V);
        //3.通过循环，如果队列不为空，则从队列中弹出一个待搜索的顶点，然后递归调用待搜索顶点邻接表中的所有顶点
        while (!waitSearch.isempty())
        {
            Integer wait = waitSearch.dequeue();
            for (Integer w : G.adj(wait)) {
                if(!marked(w))
                    BFS(G,w);
            }
        }

        //4.每次搜素都会找到一个相通的顶点，因此将相通的顶点+1
        count++;
    }

    //获取图G中与顶点V相通的所有顶点的个数
    public int count()
    {
        return count;
    }

    //判断w顶点与s顶点是否相通
    public boolean marked(int w)
    {
        return marked[w];
    }
}

由上面实现图的深度优先搜索和广度优先搜索，可以明显得到图的深度优先搜索更容易理解和编写。