实验1基于MATLAB建立控制系统数学模型

一、实验目的：

 1、掌握MATLAB语法基础

2、能够使用MATLAB建立控制系统数学模型

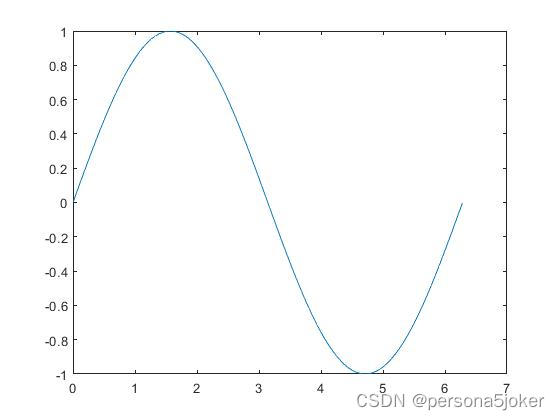
二、实验步骤：

1）→建立矩阵A=［7 8 9］，B＝[  7  ]

[  8  ]

[  9  ]

输入A=[7 8 9],B=[7;8;9]

结果：（注意分号）

A =

     7     8     9

B =

     7

     8

     9

2）→建立矩阵·B＝[1  1  2 ]

                 [ 3  5  8]

                 [ 10 12 15]

输入 B=[1 1 2; 3 5 8;10 12 15]

结果

B =

     1     1     2

     3     5     8

    10    12    15

(3)MATLAB 常用图形编辑：

编写M文件，绘制一个周期（0，2π）的正弦和余弦曲线

输入：图形编辑 >> x=linspace(0,2*pi);

>> y=sin(x);

结果

（4）、控制系统数学模型建立：

传递函数模型：在MATLAB中输入以下传递函数

1)G(S)=s+3/(s^3+2s^2+2s+1)

传递函数模型

输入 num=[1 3];

den1=[1,2,2,1];

Gtf=tf(num1,den1)

结果

Gtf =

            s+3

  ---------------------

  s^3 + 2 s^2 + 2 s + 1

2)G(5)=(s^2+4s+2)/(s^3(s^2+4)(s^2+4s))

输入num=[1,4,2];

den=conv([1,0,0,0],conv([1,0,4],[1,4,0]));

Gtf=tf(num,den)

结果

Gtf =

         s^2 + 4 s + 2

  ----------------------------

  s^7 + 4 s^6 + 4 s^5 + 16 s^4

 (5)零极点模型：在MATLAB中输入以下传递函数         

1)G(s)=10*(s+5)/(s+0.5)(s+2)(s+3)

输入：z=[-5];

p= [-0.5 -2 -3];

k=10;

G=zpk(z,p,k)

结果

G =

          10 （s + 5）

  -------------------------

  （s+0.5） (s+2) (s+3)

2)G(s)=8(s+1-j)(s+1+j)/s^2(s+5)(s+6)(s^2-1)

输入

z= [-1+i,-1-i];

p= [0,0,-5,-6,1,-1];

k=8;

G=zpk(z,p,k)

结果

G =

          8（ s+1-i） （s+1+i）

  ---------------------------------------

  s^2 ( s+5 )（s+6 ）（s+1）(s-1)

(6)控制系统模型间的相互转换

1）将系统传递函数 G(s)=(s^2+5s+6)/(s^3+2s^2+s)转换成等效的零极点模型。

输入：num=[1,5,6];

den=[1,2,1,0];

sys=tf(num,den);

[z,p,k]=tf2zp(num,den);

sys=zpk(z,p,k)

结果：

sys =

  (s+3) (s+2)

  -----------

   s (s+1)^2

2）将系统零极点模型G(s)+8(s+1)(s+2)/s(s+5)(s+6)(s+3)转换成等效的传递函数模型

输入：z= [-1,-2];

 p= [0,-5,-6,-3];

k=8;

G=zpk(z,p,k);

 G=tf(num,den)

结果

G =

       8 s^2 + 24 s + 16

  ----------------------------

  s^4 + 14 s^3 + 63 s^2 + 90 s

(7)引入反馈环节后求取传递函数

已知系统G(s)=( 2s^2+5s+1)/(s^2+2s+3),H(s)= 5(s+2)/(s+10)。求负反馈闭环传递函数。

输入num=[2 5 1];

den=[1 2 3 ];

G=tf(num ,den );

z=[-2];

p=[-10];

k=5;

H=zpk(z,p,k);

Sys=feedback(G,H,-1)

我的其他专栏：

单片机原理

模式识别原理

数字电子技术实验

自动控制原理

模拟电子技术

数据结构

关注我了解更多