本文仅作笔记学习交流，不做任何商业用途

        本文内容结合unity官方手册，唐老狮教程知识点讲解说明，如有不足还请斧正

目录

1.平时书写的向量

2.unity中的向量

2.1 一端为原点的向量

2.2 两点相减表示向量

3.向量模长和单位向量

3.1向量模长

3.2 归一化向量 = 单位向量

4.向量的乘积

4.1 点乘（内积）

正推导应用结果

逆推导求两向量夹角

4.2 叉乘（外积）

---

1.平时书写的向量

   众所周知，向量就是一个有方向的量，在纸面上我们一般在该量上画一个箭头表示，并遵从三角形法则和平行四边形法则，这里我们大概说明一下向量加减法，更多内容请参考up主一数的视频要学向量别害怕！20分钟过完基础！|神奇小猪_哔哩哔哩_bilibili：

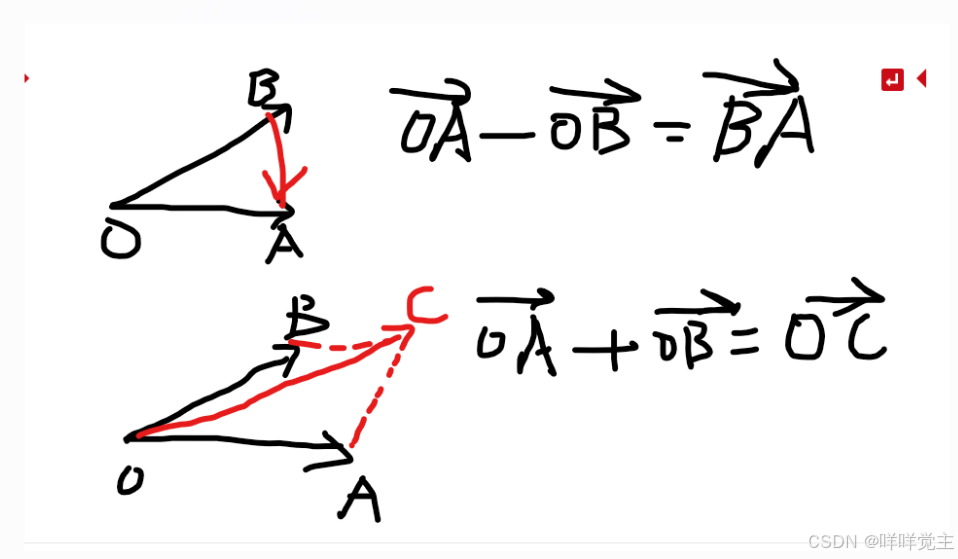
2.unity中的向量

2.1 一端为原点的向量

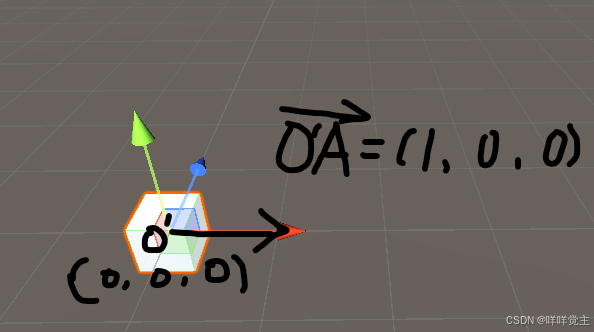
在U3d中，一个Vector3可表示一个向量，表示从(0，0，0)到该vector3的方向向量

该正方形在（0，0，0）位置

2.2 两点相减表示向量

在U3d中，一个Vector3也可表示一个点，两点相减也表示一个向量

3.向量模长和单位向量

3.1向量模长

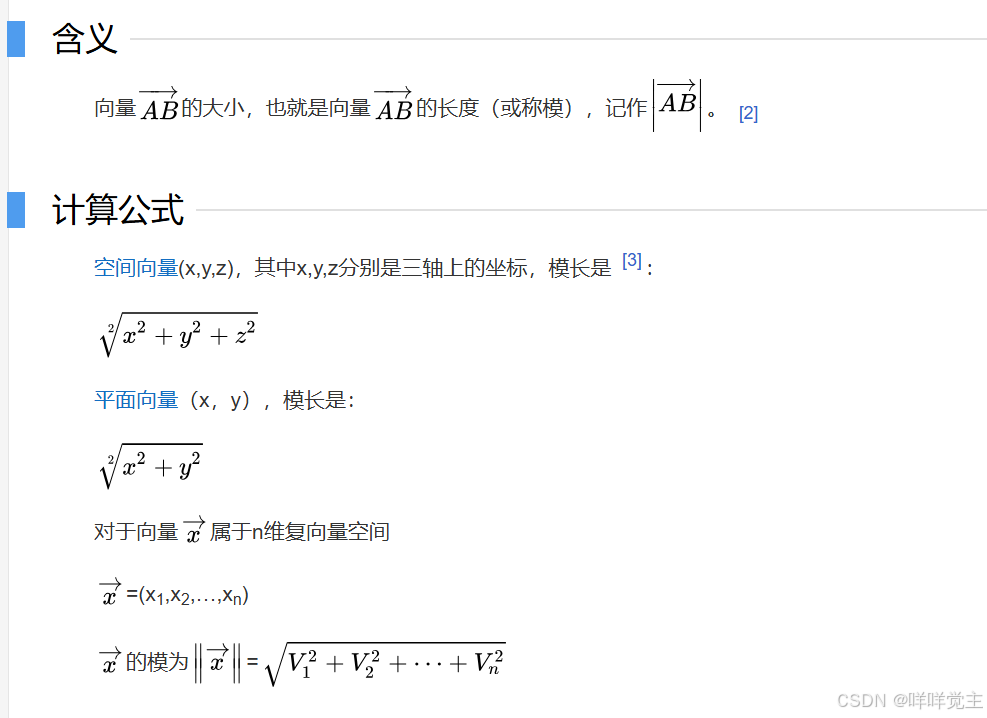
unity的api：return float

3.2 归一化向量 = 单位向量

        单位向量指的是模长（长度）为 1 的向量

比如: 

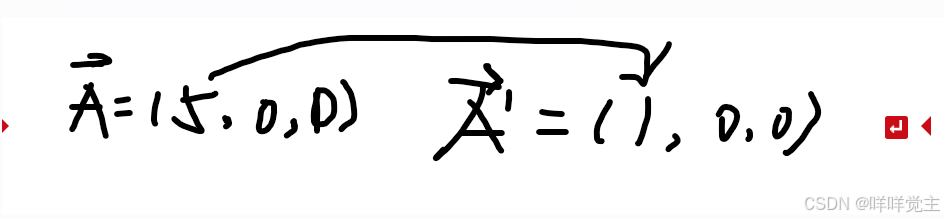
 注意 单位向量并不是说每一个数字都是1 其重点是模长=1

下图 0.71是 近似数 其平方约为0.5

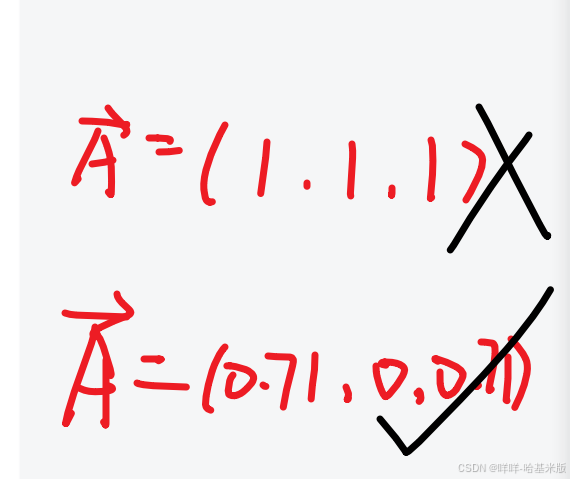
归一化公式是这样子的:

 

如果为负数做归一化 哪怕是很小的一个数字 也会改变其数字将其化作 单位向量

unity的api：return float

4.向量的乘积

4.1 点乘（内积）

正推导应用结果

向量点乘结果是一个数，下为代数和几何定义：

在unity之中我们可以利用其几何定义来判断两个向量是否大致指向同一方向

 因为两向量的夹角影响了运算结果：下红色字迹图来自唐老狮课程笔记

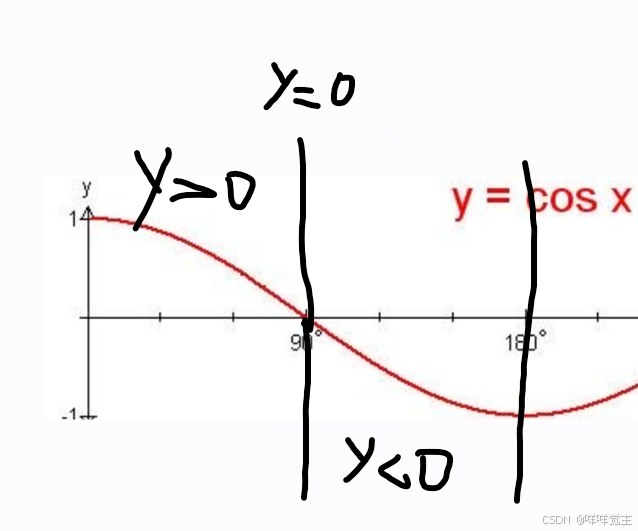
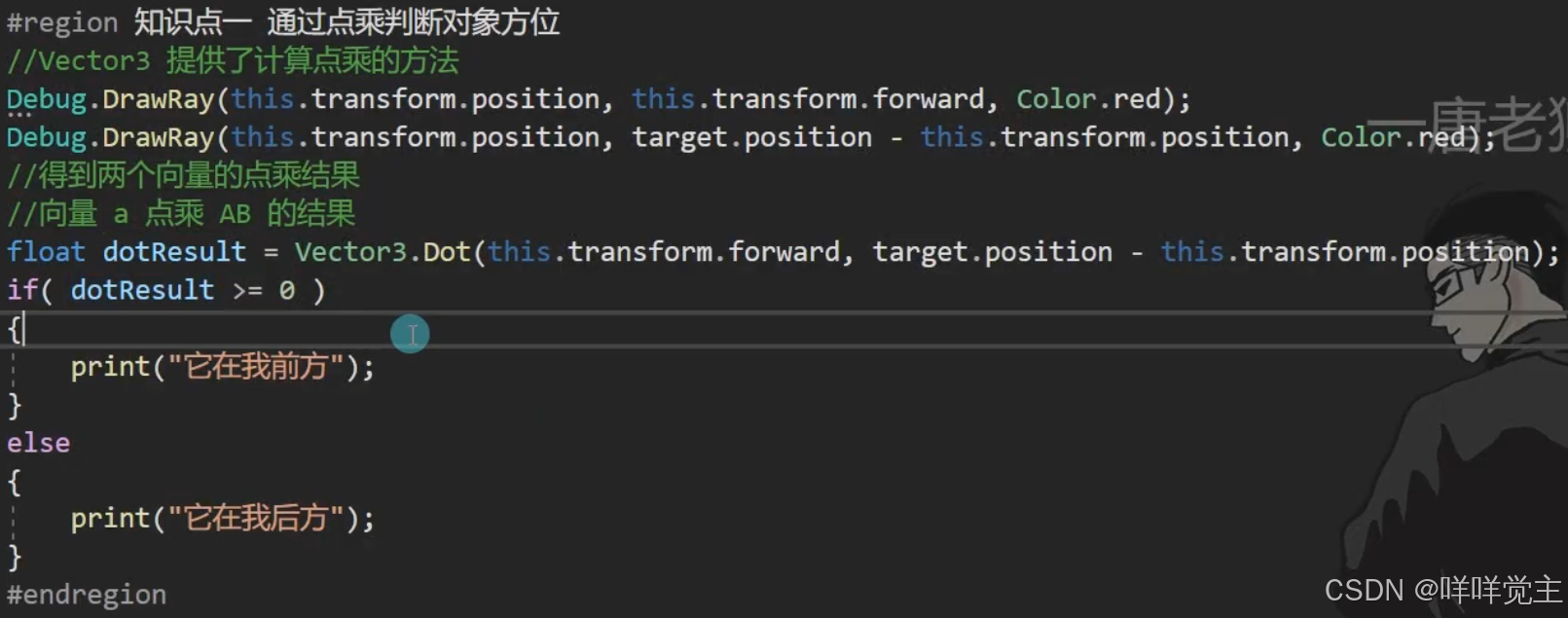
unity中可以在vector3中直接调用该静态方法：return float

 唐老狮通过画线的方法，更清晰地说明了点乘的一种应用，就不再赘述

逆推导求两向量夹角

你需要知道：向量÷该向量模长=该向量的单位向量

所以可以逆推公式得到两向量夹角：

4.2 叉乘（外积）

向量叉乘结果是一个向量，结果向量垂直于原来的两个向量,即为平面法向量

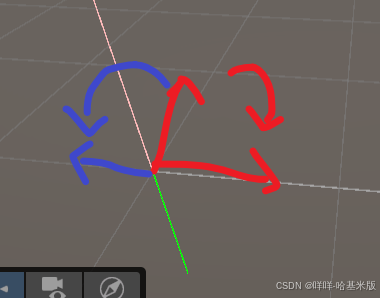
这里我要说一点，unity的空间坐标是左手坐标系 所以是左手定则

证明如下:

using UnityEngine;

namespace MieMieFrameWork
{
    public class Test : MonoBehaviour
    {
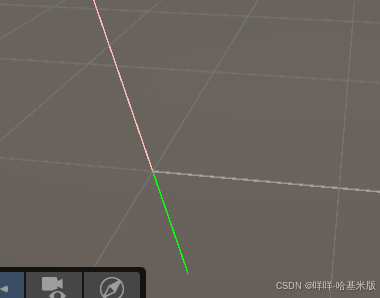
        private Vector3 vector1; // 第一个叉乘结果（红色）
        private Vector3 vector2; // 第二个叉乘结果（绿色）

        void Start()
        {
            // 计算叉乘
            vector1 = Vector3.Cross(transform.forward, transform.right).normalized;
            vector2 = Vector3.Cross(transform.forward, -transform.right).normalized;

            // 打印结果（辅助调试）
            Debug.Log($"Vector1 (红色): {vector1}"); // 预期结果：(0, 1, 0)
            Debug.Log($"Vector2 (绿色): {vector2}"); // 预期结果：(0, -1, 0)
        }

        void Update()
        {
            // 绘制红色向量（从物体位置出发，沿 vector1 方向，长度 1）
            Debug.DrawLine(transform.position, transform.position + vector1, Color.red);

            // 绘制绿色向量（从物体位置出发，沿 vector2 方向，长度 1）
            Debug.DrawLine(transform.position, transform.position + vector2, Color.green);
        }
    }
}

 

 

定义太长了啊，有需要自己看吧，注意两向量角度区间为【0，180】

向量积_百度百科 (baidu.com)

最后关于向量叉乘得到法向量的事情我们单开一篇文章说道说道