【DL学习笔记12】《深度学习进阶——自然语言处理》—— ch05: RNN

1.概率和语言模型：概率视角下的word2vec、语言模型将CBOW模型用作语言模型？；2. RNN：循环的神经网络、展开循环、Backpropagation Through Time、Truncated BPTT、Truncated BPTT的mini-batch学习；3. RNN的实现：RNN层的实现、Time RNN层的实现；4. 处理时序数据的层的实现：RNNLM的全貌图、Time层的实现

yierrrr

1124人浏览 · 2022-07-14 20:55:06

yierrrr · 2022-07-14 20:55:06 发布

Backpropagation Through Time

Truncated BPTT

Truncated BPTT的mini-batch学习

目前为止我们看到的神经网络都是前馈型神经网络。前馈(feedforward)是指网络的传播方向是单向的。但是，单纯的前馈网络无法充分学习时序数据的性质，于是RNN（Recurrent Neural Network，循环神经网络）应运而生。

1. 概率和语言模型

概率视角下的word2vec

我们先复习一下CBOW模型
- 从上下文预测目标词
- 用后验概率进行建模： $P(w_t|w_{t-1},w_{t+1})$ ，这里考虑的窗口是左右对称的
- 在仅将左侧2个单词作为上下文时： $P(w_t|w_{t-2},w_{t-1})$
- 损失函数可以写成： $L = -logP(w_t|w_{t-2},w_{t-1})$
- CBOW模型的学习旨在找到使损失函数值最小的权重参数，从而可以准确地从上下文预测目标词
- 像这样随着学习的推进，作为副产品获得了编码了单词含义信息的单词的分布式表示
那么作为CBOW模型本来的目的“从上下文预测目标词”可以发挥什么作用？

语言模型

语言模型给出了单词序列发生的概率，具体来说，就是使用概率来评估一个单词序列发生的可能性，即在多大程度上是自然的单词序列

应用：机器翻译、语音识别、生成文章
数学式表示：
- 联合概率：单词按w1，w2，…，wm的顺序出现的概率记为P(w1，w2，…，wm)
- 用后验概率分解： $\prod_{t=1}^mP(w_t|w_1,...,w_{t-1})$
- 需要注意的是，这个后验概率是以目标词左侧的全部单词为上下文时的概率
- 由 $P(w_t|w_1,...,w_{t-1})$ 表示的模型称为条件语言模型

将CBOW模型用作语言模型？

我们通过将上下文的大小限制在某个值来近似实现
CBOW模型的上下文大小可以任意设定，但是CBOW模型还存在忽视了上下文中单词顺序的问题，因为CBOW模型的中间层是单词向量的和
为此，我们想要考虑顺序时，应该在中间层拼接上下文的单词向量，但是这会是参数的数量增加
这时RNN出场，无论上下文有多长，都可以将上下文信息记住，因此RNN可以处理任意长度的时序数据

2. RNN

循环的神经网络

RNN的特征就在于拥有一个环路，可以使数据不断循环，通过数据的循环，RNN可以一边记住过去的数据，一边更新到最新的数据

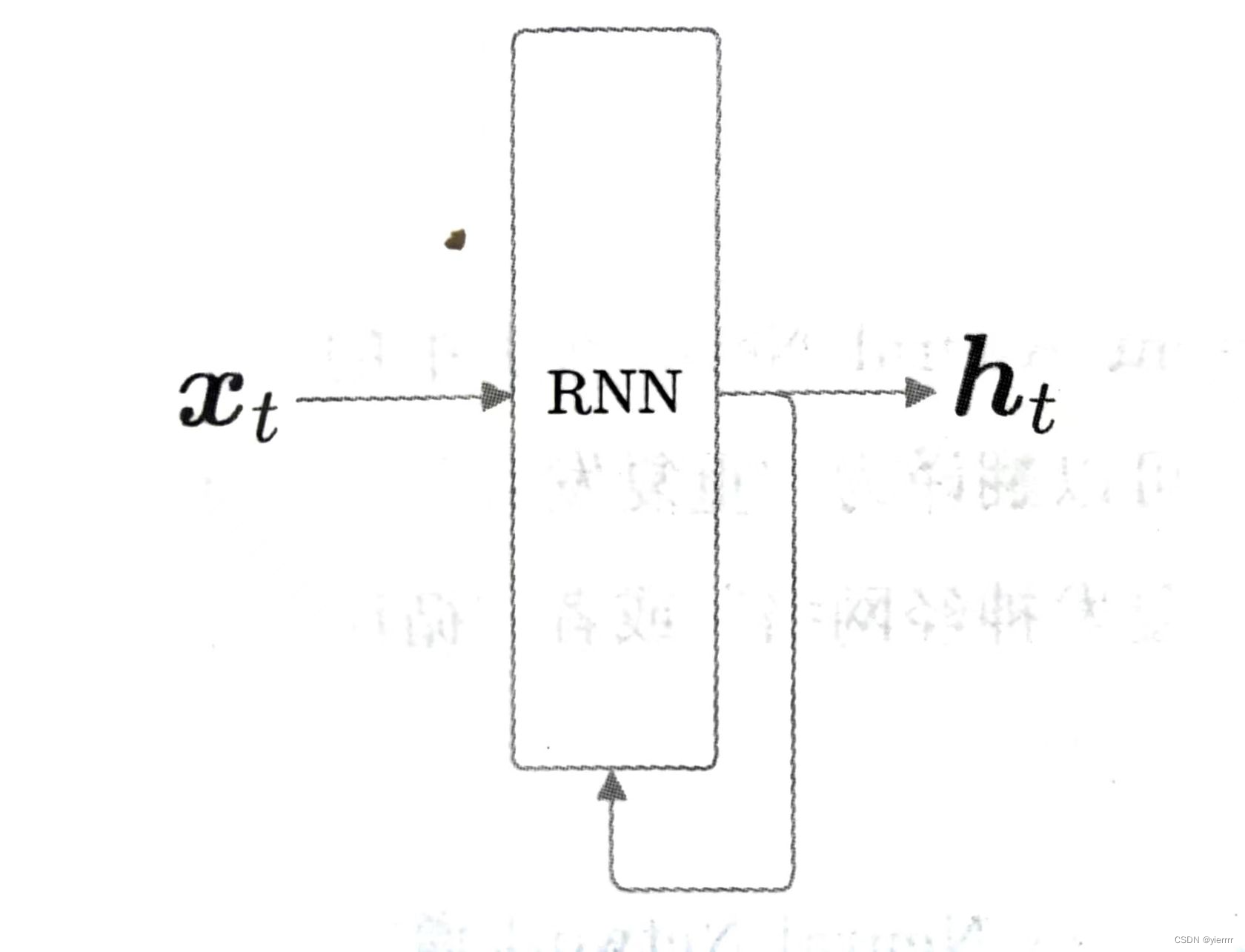
时刻t的输入使x_t，暗示着时许数据（x1，x2，…，xt）会被输入到层，然后以与输入对应的形式，输出（h1，h2，…，ht）。比如在处理句子时，将各个单词的分布式表示作为xt输入到RNN层
输出有两个分叉，意味着同一个东西被复制了，其中一个分叉成为其自身的输入

展开循环

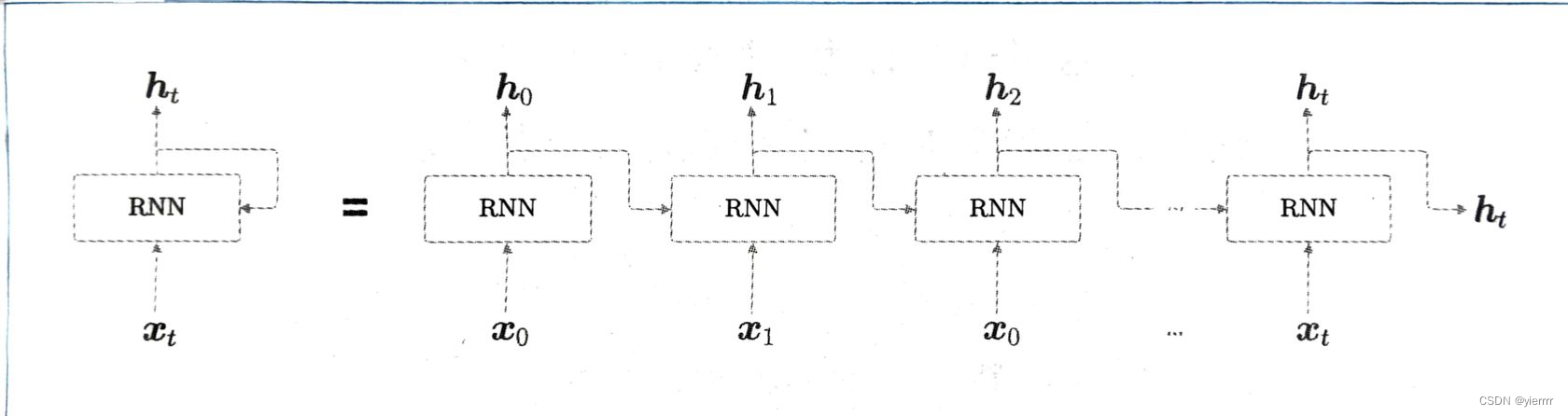
展开后，可以看到和前馈神经网络相同的结构，不过这里的RNN层都是在同一层中
时序数据按时间顺序排序，因此我们用“时刻”指代时序数据的索引
各个时刻的RNN层接收传给该层的输入和前一个RNN层的输出
- 公式： $h_t=tanh(h_{t-1}W_h+x_tW_x+b)$
- RNN有两个权重，分别是输入x转化为输出h的权重Wx和将前一个RNN层的输出转化为当前时刻的输出的权重Wh
- 首先执行矩阵的乘积计算，然后使用tanh函数（双曲正切函数）变换它们的和，其结果就是时刻t的输出ht（隐藏状态）
- ht一方面向上输出到另一个层，另一方面向右输出到下一个RNN层（自身）
可以说，RNN具有状态h，并以公式的形式被更新，这就是说RNN是具有状态的层或具有存储的层的原因
时刻t的输出ht被称为隐藏状态或隐藏状态向量

Backpropagation Through Time

将循环展开后的RNN可以通过先进行正向传播，再进行反向传播的方式求目标梯度。因为是“按时间顺序展开的神经网络的误差反向传播法”，所以称为Backpropagation Through Time（基于时间的反向传播，BPTT）

存在问题：随着时序数据的时间跨度的增大，BPTT消耗的计算机资源也会成比例增大，反向传播的梯度也会变得不稳定。因为要保存各个时刻的RNN层的中间数据

Truncated BPTT

在处理长时序数据时，通常的做法是将网络连接截成适当的长度。具体来说，就是将时间轴方向上过长的网络在合适的位置进行截断，从而创建多个小型网络，然后对截出来的小型网络执行误差反向传播法

将反向传播的连接中的某一段RNN层称为“块”
严格来说，只是反向传播的连接被截断，正向传播的连接依然被维持
因此进行RNN学习时，必须考虑正向传播之间是有关联的，这意味着必须按顺序输入数据。之前的神经网络在进行mini-batch学习时，数据都是随机选择的
按顺序学习的重点：正向传播的计算需要前一个块最后的隐藏状态

Truncated BPTT的mini-batch学习

在输入数据的开始位置，需要在各个批次中进行“偏移”
例如，对长度为1000的时序数据，以时间长度10为单位进行阶段，批大小设为2进行学习。此时第1笔样本数据从头开始按顺序输入，第2笔数据从第500个数据开始按顺序输入，也就是说，将开始位置平移500

3. RNN的实现

RNN层的实现

公式： $h_t=tanh(h_{t-1}W_h+x_tW_x+b)$
实现：

class RNN:
    def __init__(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None  # 反向传播时要用到的中间数据

    def forward(self, x, h_prev):
        Wx, Wh, b = self.params
        t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
        h_next = np.tanh(t)

        self.cache = (x, h_prev, h_next)
        return h_next

    def backward(self, dh_next):
        Wx, Wh, b = self.params
        x, h_prev, h_next = self.cache

        dt = dh_next * (1 - h_next ** 2)
        db = np.sum(dt, axis=0)
        dWh = np.dot(h_prev.T, dt)
        dh_prev = np.dot(dt, Wh.T)
        dWx = np.dot(x.T, dt)
        dx = np.dot(dt, Wx.T)

        self.grads[0][...] = dWx
        self.grads[1][...] = dWh
        self.grads[2][...] = db

        return dx, dh_prev

Time RNN层的实现

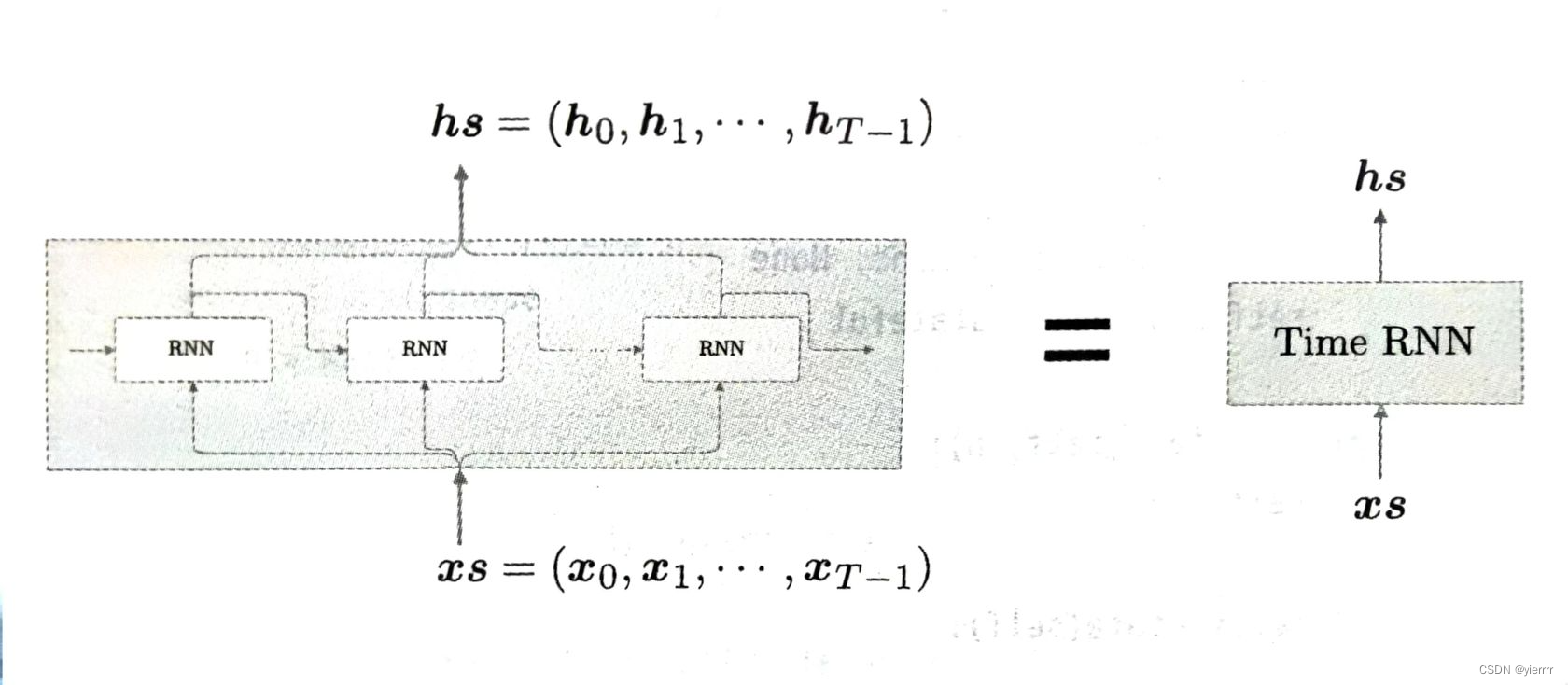
T目标神经网络接受长度为T的时序数据，输出各个时刻的隐藏状态T个，这里考虑到模块化，将输入和输出分别捆绑在一起，就可以将水平排列的展开循环后的层视为一个层
这里我们将进行Time RNN层中的单步处理的层称为“RNN层”，将一次处理T步的层称为“Time RNN层”

class TimeRNN:
    def __init__(self, Wx, Wh, b, stateful=False):
        """

        @param Wx: 输入x转化为输出h的权重
        @param Wh: 前一个RNN层的输出转化为当前时刻的输出的权重
        @param b: 偏置
        @param stateful: 控制是否继承隐藏状态，长时序数据需要维持RNN的隐藏状态
        """
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.layers = None  # 保存多个RNN层
        self.h = None  # 保存调用forward()方法时的最后一个RNN层的隐藏状态
        self.dh = None  # 保存传给前一个块的隐藏状态的梯度
        self.stateful = stateful

    def forward(self, xs):  # xs包括了T个时序数据
        Wx, Wh, b = self.params
        N, T, D = xs.shape  # N是批大小，D是输入向量的维数
        D, H = Wx.shape

        self.layers = []
        hs = np.empty((N, T, H), dtype='f')  # 为输出准备一个“容器”

        # 在首次调用时(h为None时)，RNN层的隐藏状态h由所有元素均为0的矩阵初始化
        # 在stateful为False的情况下，h将总是被重置为零矩阵，即不继承隐藏状态
        if not self.stateful or self.h is None:
            self.h = np.zeros((N, H), dtype='f')

        # T次for循环，生成RNN层
        for t in range(T):
            layer = RNN(*self.params)
            self.h = layer.forward(xs[:, t, :], self.h)
            hs[:, t, :] = self.h  # 存放各个时刻的隐藏状态
            self.layers.append(layer)

        return hs

    def backward(self, dhs):
        Wx, Wh, b = self.params
        N, T, H = dhs.shape
        D, H = Wx.shape

        dxs = np.empty((N, T, D), dtype='f')
        dh = 0
        grads = [0, 0, 0]
        for t in reversed(range(T)):
            layer = self.layers[t]
            # backward的输入是从输出侧传来的梯度dhs和下一时刻的隐藏状态的梯度dh求和
            # 输出有流向输入侧的梯度dx和流向上一时刻的隐藏状态的梯度dh
            dx, dh = layer.backward(dhs[:, t, :] + dh)
            dxs[:, t, :] = dx

            # 每个RNN层使用相同的权重，因此最终的权重梯度是各个RNN层的权重梯度之和
            for i, grad in enumerate(layer.grads):
                grads[i] += grad
        # 用最终结果覆盖成员变量
        for i, grad in enumerate(grads):
            self.grads[i][...] = grad
        self.dh = dh

        return dxs

    # 考虑拓展性，可以设定隐藏状态
    def set_state(self, h):
        self.h = h

    # 重设隐藏状态
    def reset_state(self):
        self.h = None

4. 处理时序数据的层的实现

本章我们的目标是使用RNN实现语言模型（RNNLM），目前我们已经实现了RNN层和整体处理时序数据的Time RNN层

RNNLM的全貌图

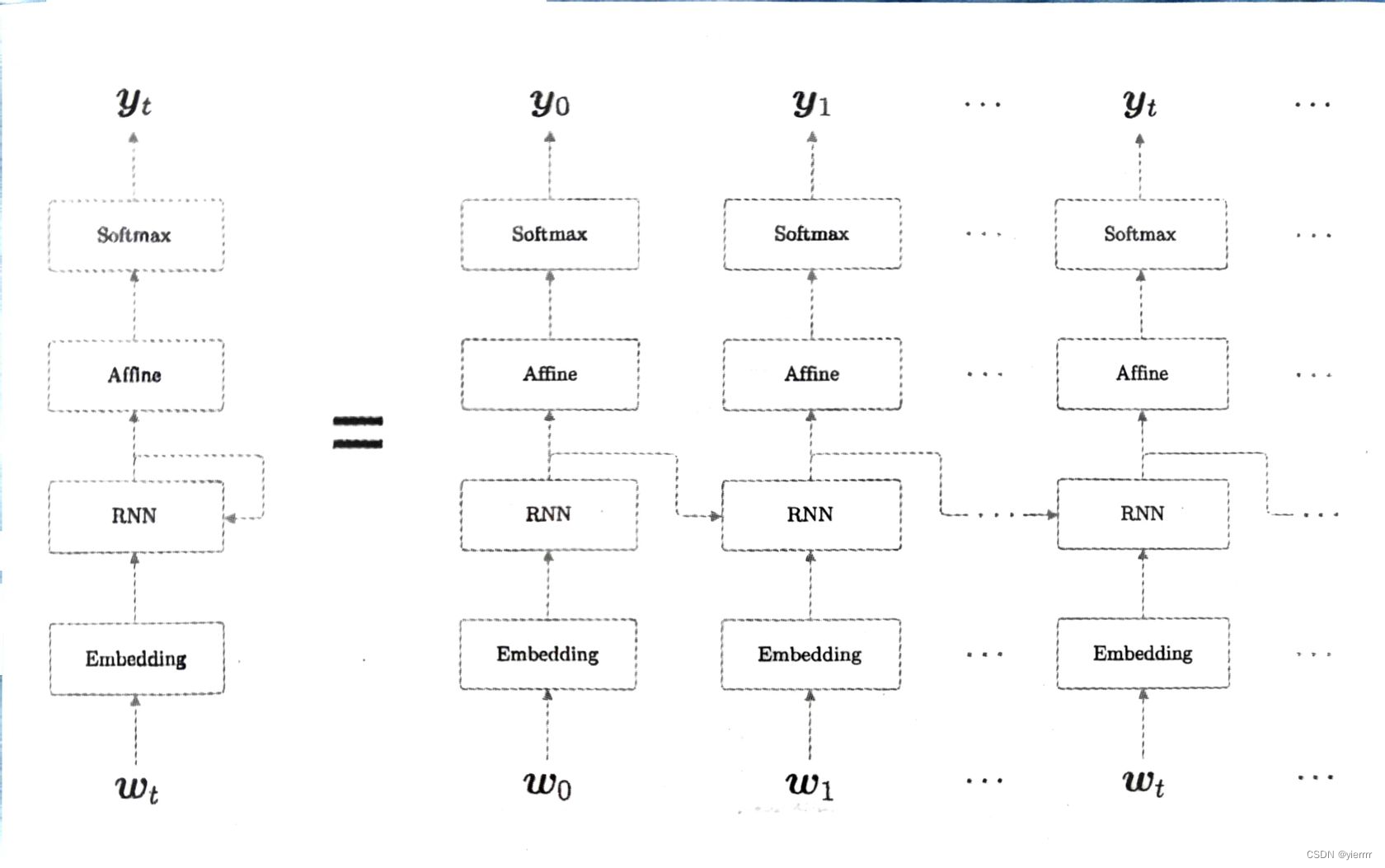
第1层Embedding层，将单词ID转化为单词的分布式表示（向量）然后输入到RNN层
第2层RNN层向下一层输出隐藏状态，同时向下一时刻的RNN层输出隐藏状态
RNN层向上方输出的隐藏状态经过Affine层，传给Softmax层

当我们仅考虑正向传播，传入”you say goodbye and i say hello.“时，RNNLM进行的处理如图所示

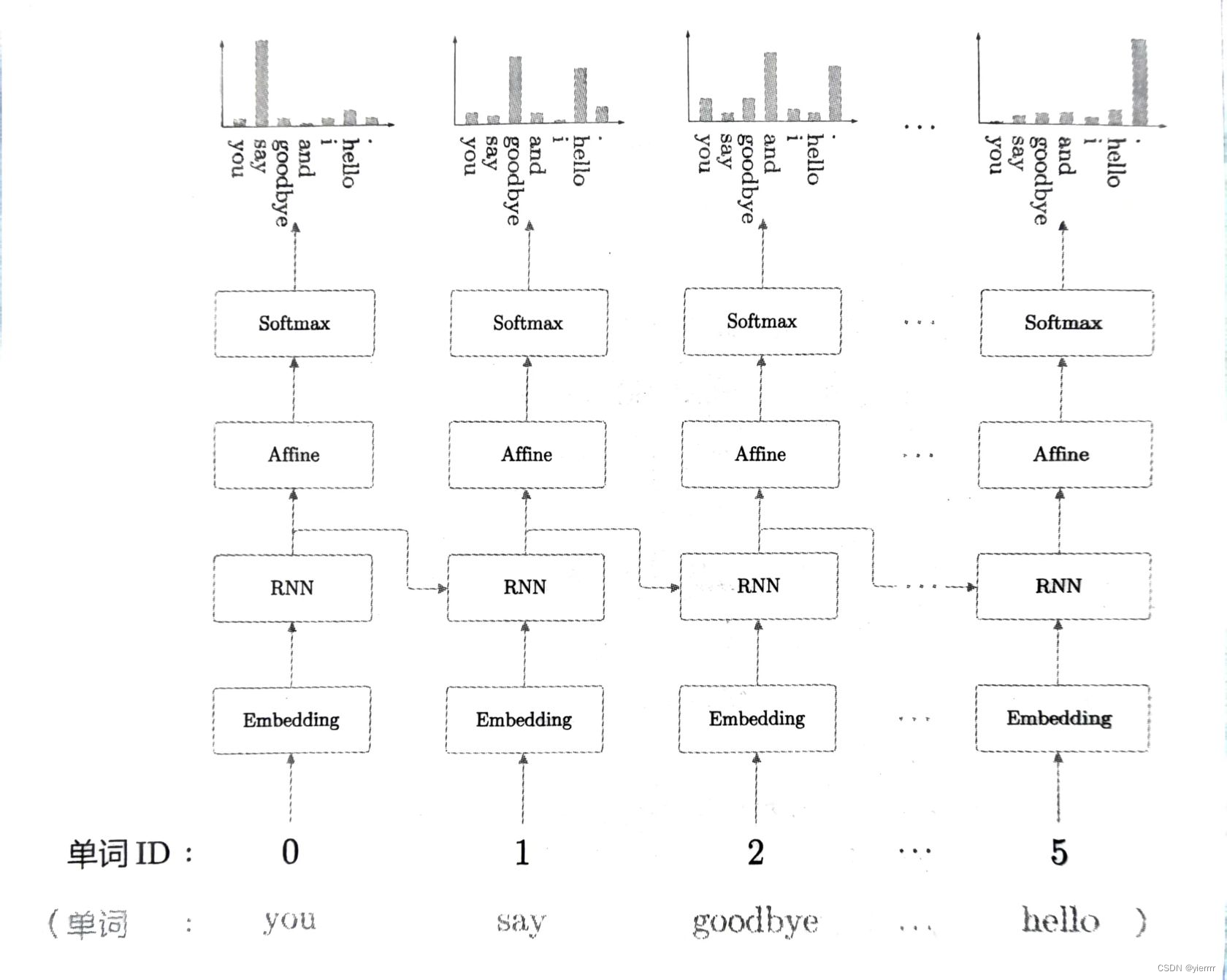
RNNLM可以”记忆“目前为止输入的单词，并以此为基础预测接下来会出现的单词
RNN层通过从过去到现在继承并传递数据，使得编码和存储过去的信息成为可能

Time层的实现

将整体处理时序数据的层实现为Time XX层

Time Affine层

class TimeAffine:
    def __init__(self, W, b):
        self.params = [W, b]
        self.grads = [np.zeros_like(W), np.zeros_like(b)]
        self.x = None

    def forward(self, x):
        N, T, D = x.shape
        W, b = self.params

        rx = x.reshape(N*T, -1)
        out = np.dot(rx, W) + b
        self.x = x
        return out.reshape(N, T, -1)

    def backward(self, dout):
        x = self.x
        N, T, D = x.shape
        W, b = self.params

        dout = dout.reshape(N*T, -1)
        rx = x.reshape(N*T, -1)

        db = np.sum(dout, axis=0)
        dW = np.dot(rx.T, dout)
        dx = np.dot(dout, W.T)
        dx = dx.reshape(*x.shape)

        self.grads[0][...] = dW
        self.grads[1][...] = db

        return dx

Time Embedding层

class TimeEmbedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.layers = None
        self.W = W

    def forward(self, xs):
        N, T = xs.shape
        V, D = self.W.shape

        out = np.empty((N, T, D), dtype='f')
        self.layers = []

        for t in range(T):
            layer = Embedding(self.W)
            out[:, t, :] = layer.forward(xs[:, t])
            self.layers.append(layer)

        return out

    def backward(self, dout):
        N, T, D = dout.shape

        grad = 0
        for t in range(T):
            layer = self.layers[t]
            layer.backward(dout[:, t, :])
            grad += layer.grads[0]

        self.grads[0][...] = grad
        return None

TimeSoftmaxWithLoss层
- T个SoftmaxWithLoss层各自算出损失，然后加在一起去平均得到最后的损失

class TimeSoftmaxWithLoss:
    def __init__(self):
        self.params, self.grads = [], []
        self.cache = None
        self.ignore_label = -1

    def forward(self, xs, ts):
        N, T, V = xs.shape

        if ts.ndim == 3:  # 在监督标签为one-hot向量的情况下
            ts = ts.argmax(axis=2)

        mask = (ts != self.ignore_label)

        # 按批次大小和时序大小进行整理（reshape）
        xs = xs.reshape(N * T, V)
        ts = ts.reshape(N * T)
        mask = mask.reshape(N * T)

        ys = softmax(xs)
        ls = np.log(ys[np.arange(N * T), ts])
        ls *= mask  # 与ignore_label相应的数据将损失设为0
        loss = -np.sum(ls)
        loss /= mask.sum()

        self.cache = (ts, ys, mask, (N, T, V))
        return loss

    def backward(self, dout=1):
        ts, ys, mask, (N, T, V) = self.cache

        dx = ys
        dx[np.arange(N * T), ts] -= 1
        dx *= dout
        dx /= mask.sum()
        dx *= mask[:, np.newaxis]  # 与ignore_label相应的数据将梯度设为0

        dx = dx.reshape((N, T, V))

        return dx

5. RNNLM的学习和评价

class SimpleRnnlm:
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        V, D, H = vocab_size, wordvec_size, hidden_size
        rn = np.random.randn

        # 初始化权重
        embed_W = (rn(V, D) / 100).astype('f')
        rnn_Wx = (rn(D, H) / np.sqrt(D)).astype('f')
        rnn_Wh = (rn(H, H) / np.sqrt(H)).astype('f')
        rnn_b = np.zeros(H).astype('f')
        affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
        affine_b = np.zeros(V).astype('f')

        # 生成层
        self.layers = [
            TimeEmbedding(embed_W),
            TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
            TimeAffine(affine_W, affine_b)
        ]
        self.loss_layer = TimeSoftmaxWithLoss()
        self.rnn_layer = self.layers[1]

        # 将所有的权重和梯度整理到列表中
        self.params, self.grads = [], []
        for layer in self.layers:
            self.params += layer.params
            self.grads += layer.grads

    def forward(self, xs, ts):
        for layer in self.layers:
            xs = layer.forward(xs)
        loss = self.loss_layer.forward(xs, ts)
        return loss

    def backward(self, dout=1):
        dout = self.loss_layer.backward(dout)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)
        return dout

    def reset_state(self):
        self.rnn_layer.reset_state()

其中Affine层和RNN层使用了”Xavier初始值“

语言模型的评价

语言模型基于给定的已经出现的单词输出将要出现的单词的概率分布。
困惑度(perplexity)表示”概率的倒数”，常被用作评价语言模型的预测性能的指标。困惑度越小，表明模型越好
在输入数据为多个的情况下：
- $p=e^L,L=-\frac{1}{N}\sum_n\sum_kt_{nk}logy_{nk}$
- 假设数据量为N个，tn是one-hot向量形式的正确解标签，tnk表示第n个数据的第k个值，ynk表示概率分布（神经网络中的Softmax的输出）

RNNLM的学习代码

和之前神经网络的学习基本上是一样的，但有两点不同：
- 数据的输入方式：使用Truncated BPTT进行学习，数据要求按顺序输入，并且mini-batch的各批次要平移读入数据的开始位置
- 困惑度的计算：计算每个epoch的困惑度，首先要计算每个epoch的平均损失

# 设定超参数
batch_size = 10
wordvec_size = 100
hidden_size = 100
time_size = 5  # Truncated BPTT的时间跨度大小
lr = 0.1
max_epoch = 100

# 读入训练数据（缩小了数据集）
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)

xs = corpus[:-1]  # 输入
ts = corpus[1:]  # 输出（监督标签）
data_size = len(xs)
print('corpus size: %d, vocabulary size: %d' % (corpus_size, vocab_size))

# 学习用的参数
max_iters = data_size // (batch_size * time_size)
time_idx = 0
total_loss = 0
loss_count = 0
ppl_list = []

# 生成模型
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)

# 计算读入mini-batch的各笔样本数据的开始位置(偏移量)
jump = (corpus_size - 1) // batch_size
offsets = [i * jump for i in range(batch_size)]

for epoch in range(max_epoch):
    for iter in range(max_iters):
        # 获取mini-batch
        # 首先准备容器batch_x和batch_t
        batch_x = np.empty((batch_size, time_size), dtype='i')
        batch_t = np.empty((batch_size, time_size), dtype='i')
        # 然后依次增加time_idx，将time_idx处的数据从语料库中取出
        for t in range(time_size):
            for i, offset in enumerate(offsets):
                # 当读入语料库的位置超过语料库大小是，要回到语料库的开头处
                batch_x[i, t] = xs[(offset + time_idx) % data_size]
                batch_t[i, t] = ts[(offset + time_idx) % data_size]
            time_idx += 1

        # 计算梯度，更新参数
        loss = model.forward(batch_x, batch_t)
        model.backward()
        optimizer.update(model.params, model.grads)
        total_loss += loss
        loss_count += 1

    # 各个epoch的困惑度评价
    ppl = np.exp(total_loss / loss_count)
    print('| epoch %d | perplexity %.2f'
          % (epoch+1, ppl))
    ppl_list.append(float(ppl))
    total_loss, loss_count = 0, 0

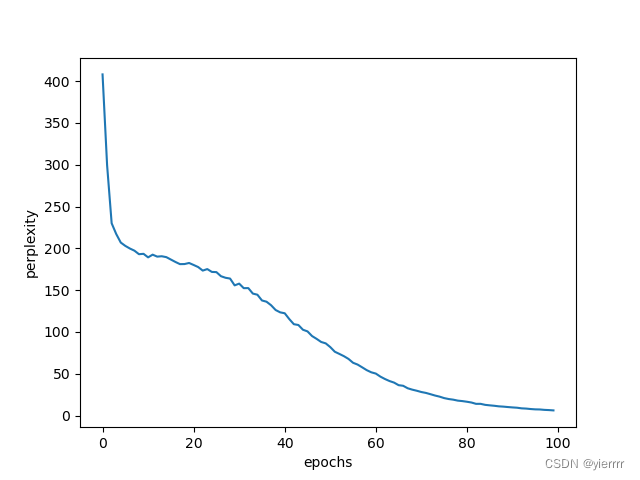
# 绘制图形
x = np.arange(len(ppl_list))
plt.plot(x, ppl_list, label='train')
plt.xlabel('epochs')
plt.ylabel('perplexity')
plt.show()

RNNLM的Trainer类

内部封装了刚才的RNNLM的学习

# 设定超参数
batch_size = 10
wordvec_size = 100
hidden_size = 100  # RNN的隐藏状态向量的元素个数
time_size = 5  # RNN的展开大小
lr = 0.1
max_epoch = 100

# 读入训练数据
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000  # 缩小测试用的数据集
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)
xs = corpus[:-1]  # 输入
ts = corpus[1:]  # 输出（监督标签）

# 生成模型
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)

trainer.fit(xs, ts, max_epoch, batch_size, time_size)
trainer.plot()

首先使用model和optimizer初始化RnnlmTrainer类，然后调用fit()完成学习

技术共进，成长同行——讯飞AI开发者社区

更多推荐

论文笔记：AlphaEdit: Null-Space Constrained Knowledge Editing for Language Models（AlphaEdit）

论文发表于人工智能顶会ICLR（基于定位和修改的模型编辑方法（针对和等）会破坏LLM中最初保存的知识，特别是在顺序编辑场景。为此，本文提出AlphaEdit：1、在将保留知识应用于参数之前，将扰动投影到保留知识的零空间上。2、从理论上证明，这种预测确保了在查询保留的知识时，编辑后的LLM的输出保持不变，从而减轻中断问题。3、对各种LLM（包括LLaMA3、GPT2XL和GPT-J）的广泛实验表明，