反向传播算法代码实现(基于python且不使用框架)

–作者：就是我自己

摘要

本文致力于对反向传播算法的原理代码实现，因此代码设计部分不会使用任何的神经网络框架，为读者刨析反向传播算法最底层的原理，而且对于理论部分的知识会相对粗略地进行介绍，如果你是已经完全了解反向传播算法原理的同学，可以直接跳转到附录的代码汇总部分

运行环境依赖

• numpy
• python3
  

运行结果

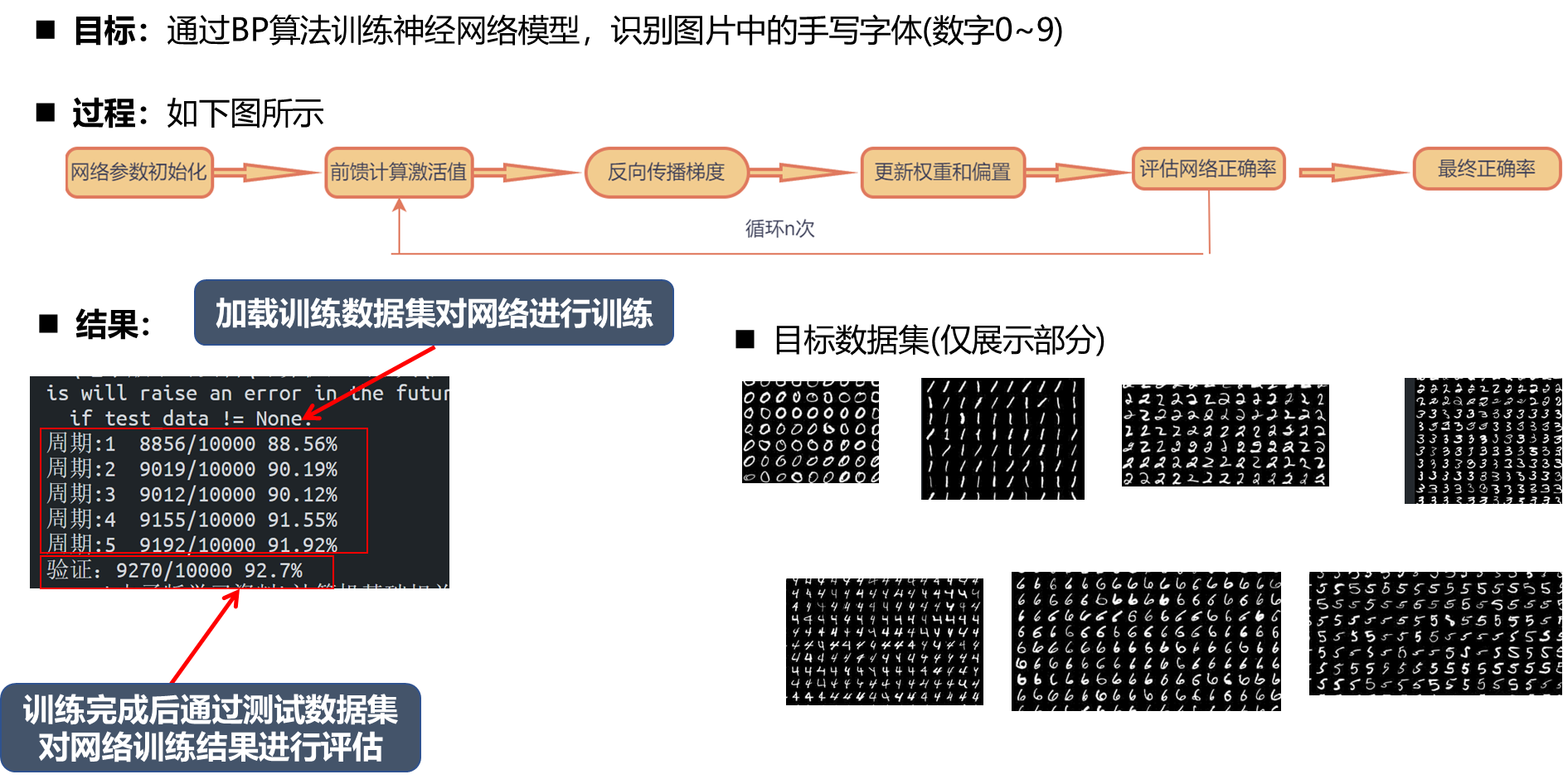
通用近似定理

前向传播激活值

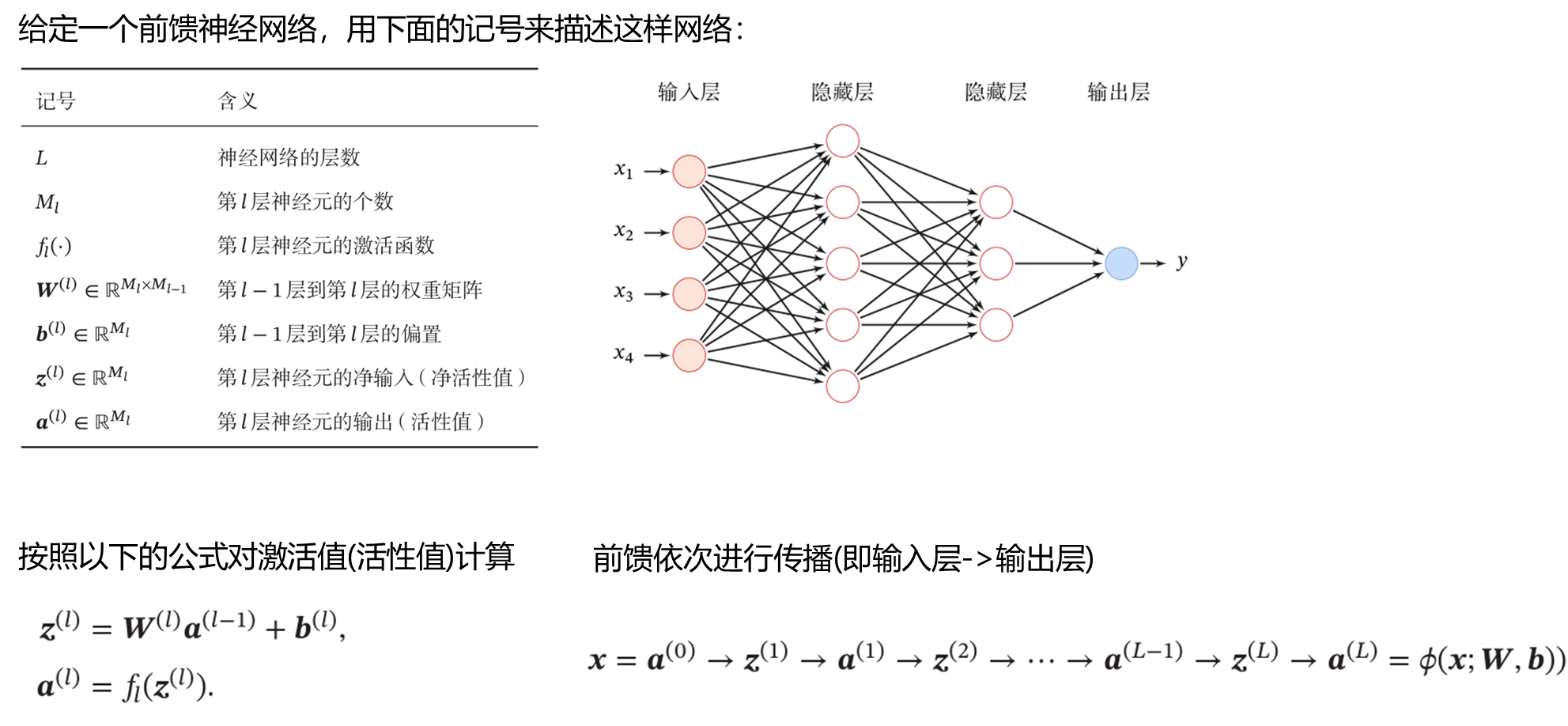
参数学习

梯度下降示意

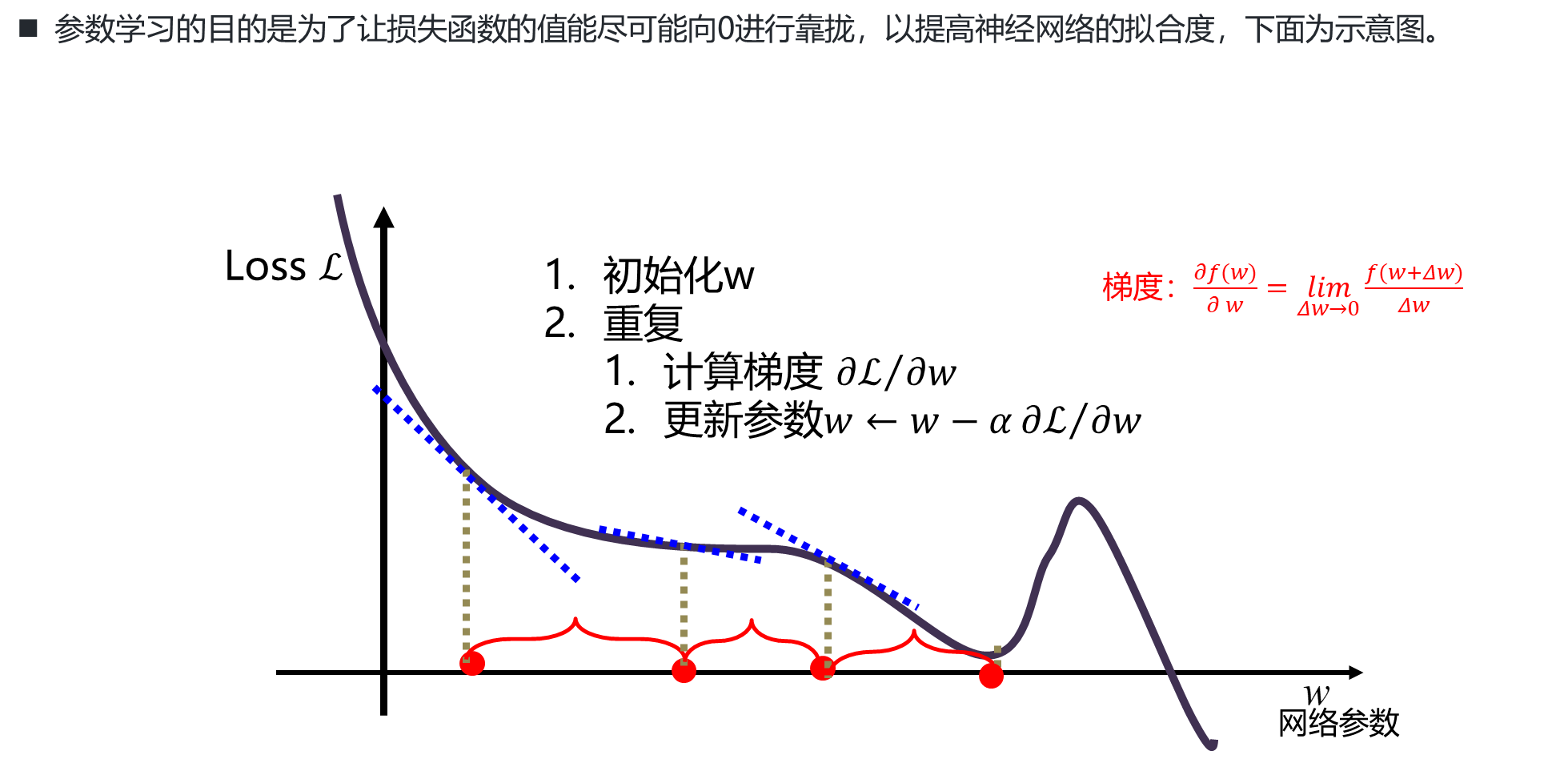
反向传播算法

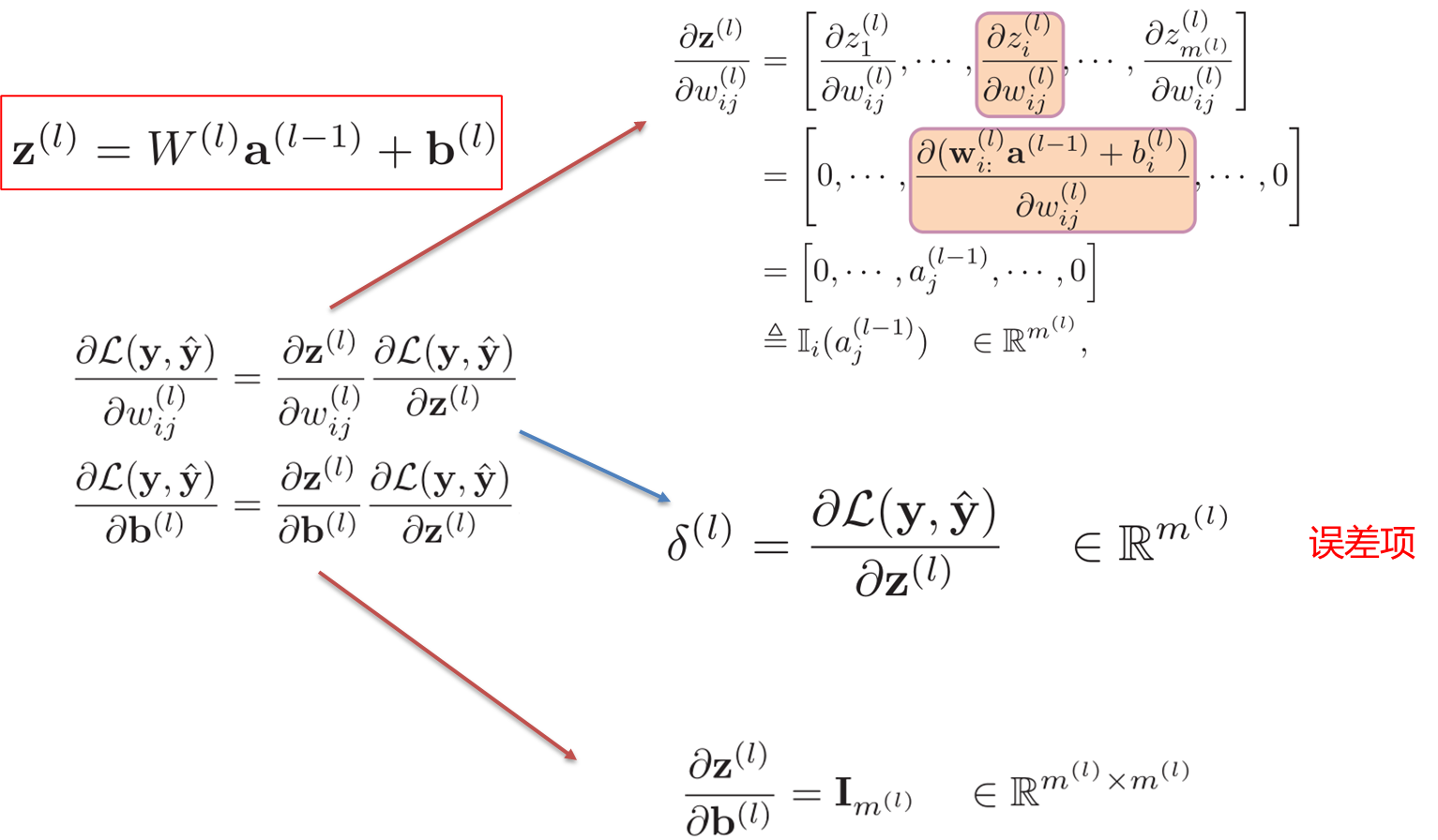
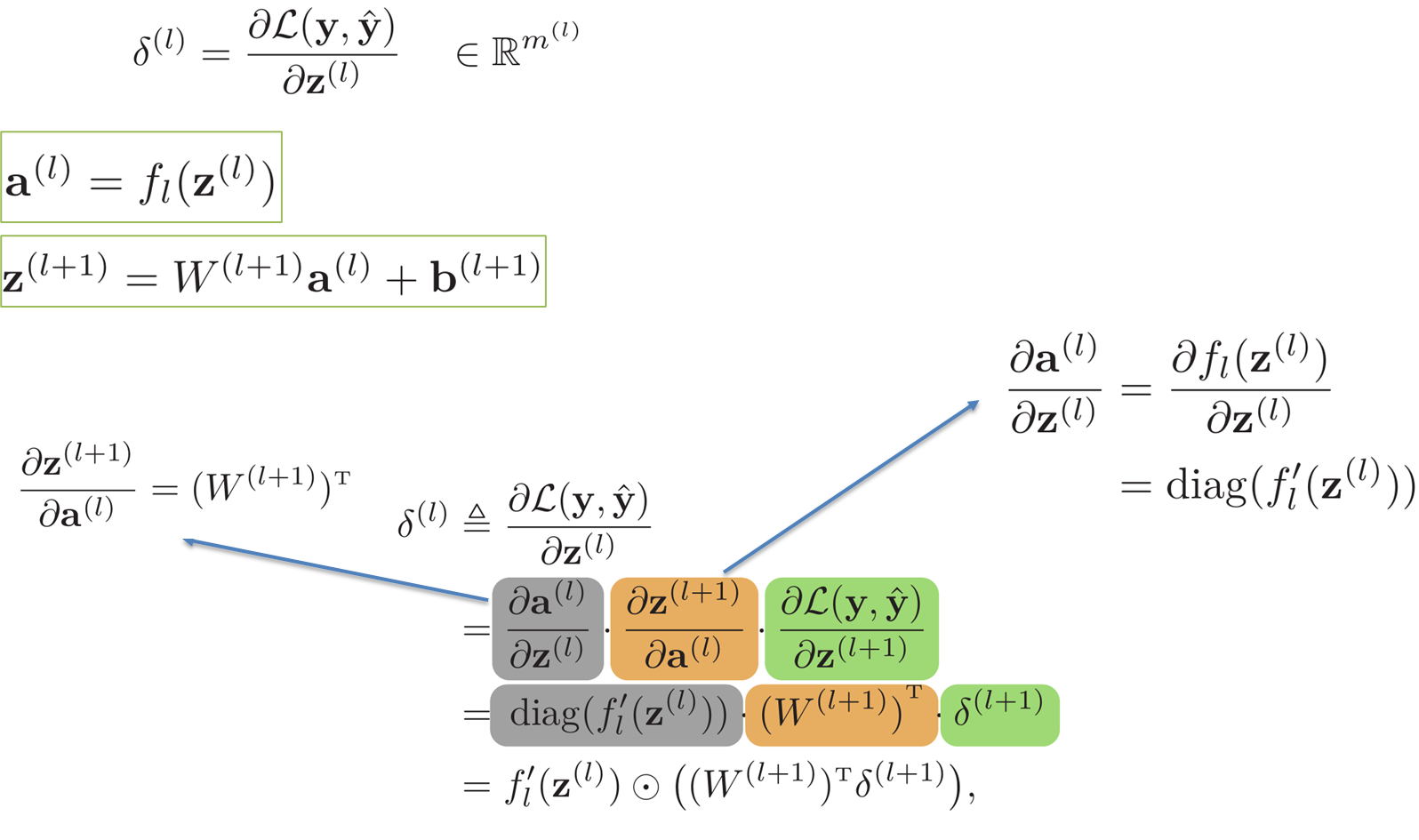
公式推导结论

激活函数设计

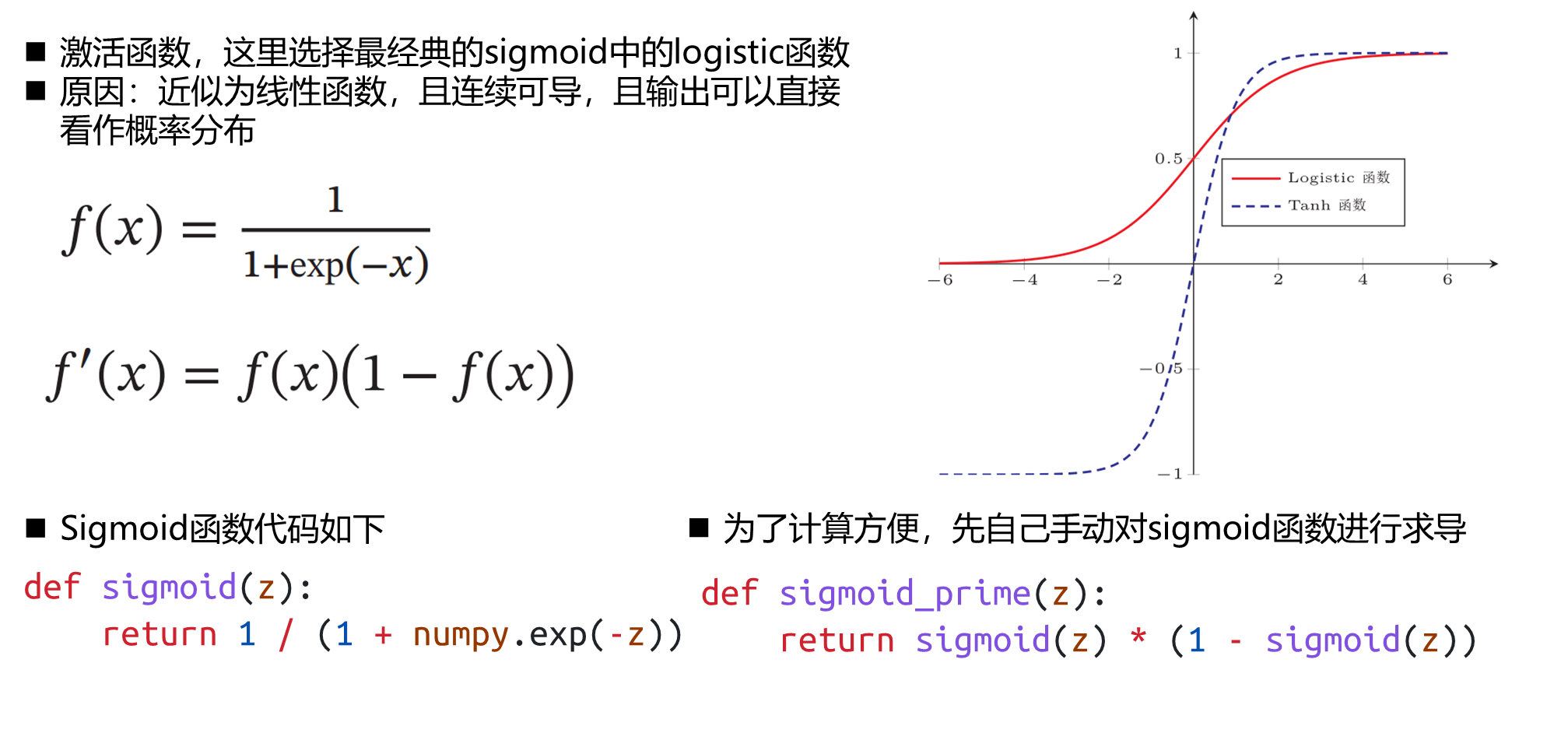
神经网络类设计

网络参数初始化

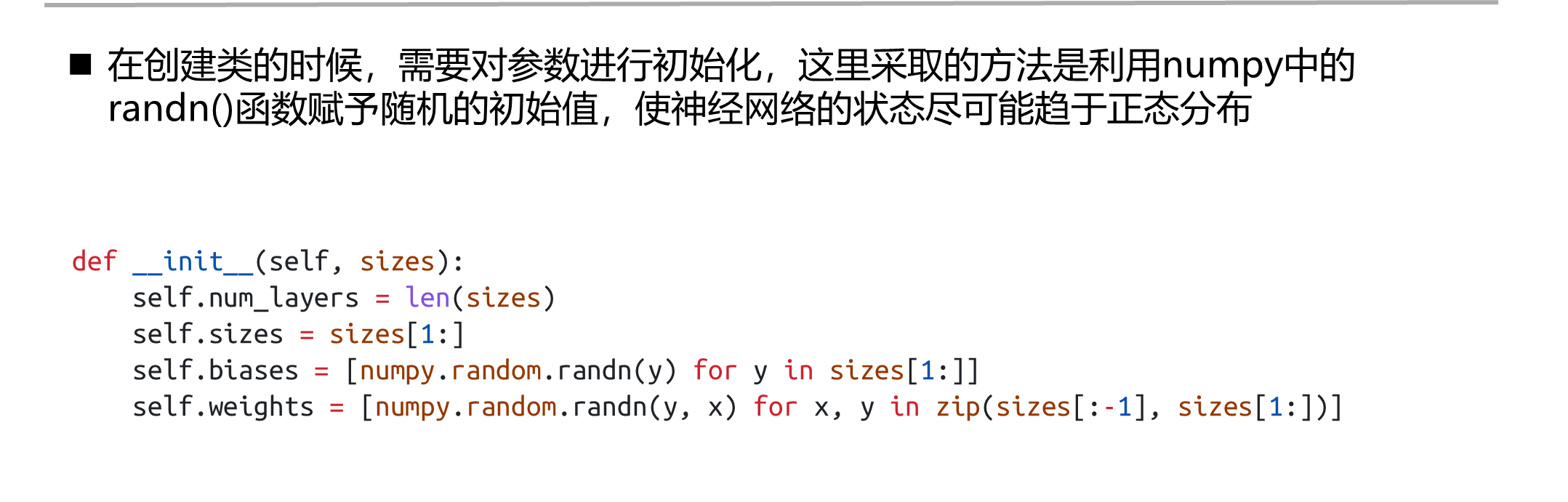
激活值与代价计算

梯度计算(核心部分)

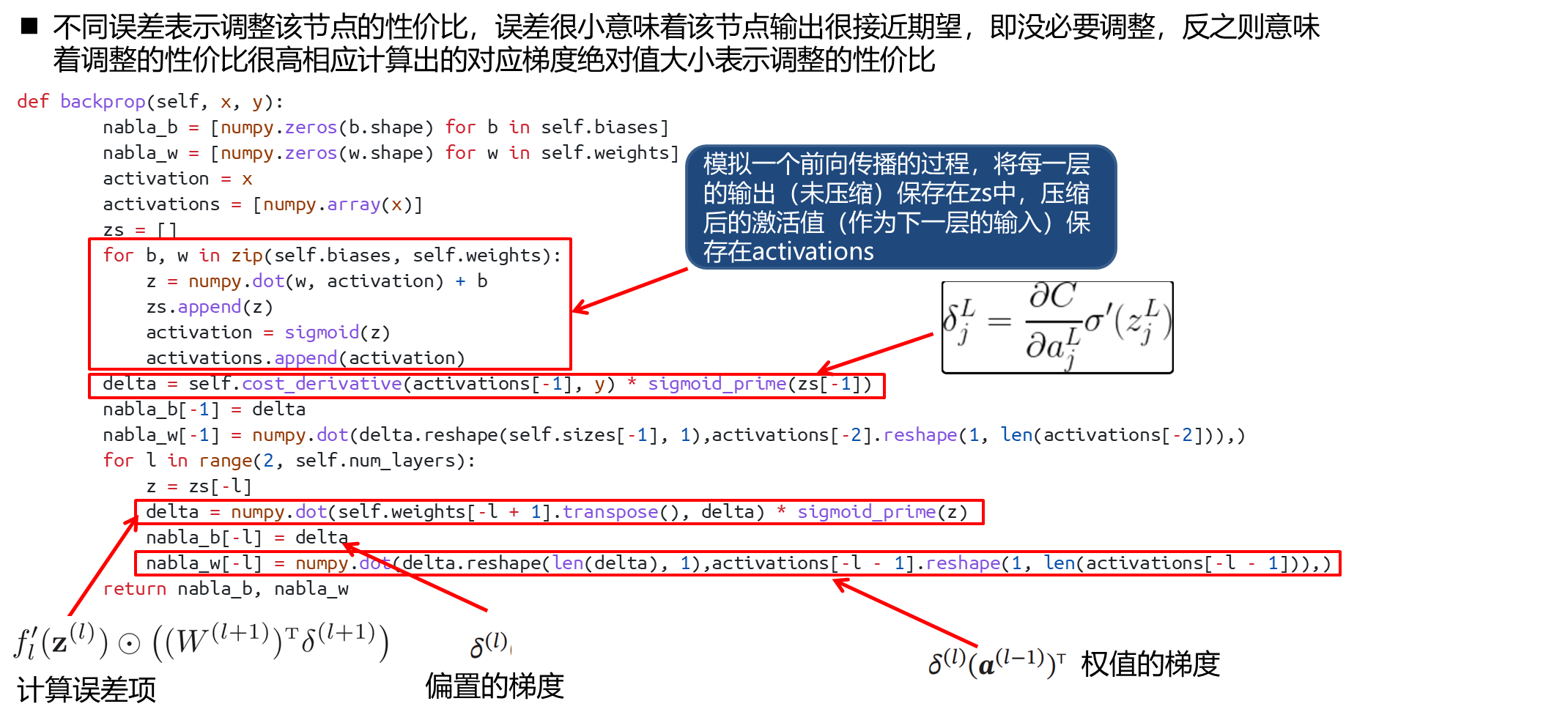
更新权重与偏置

模型评估

模型训练

保存模型数据

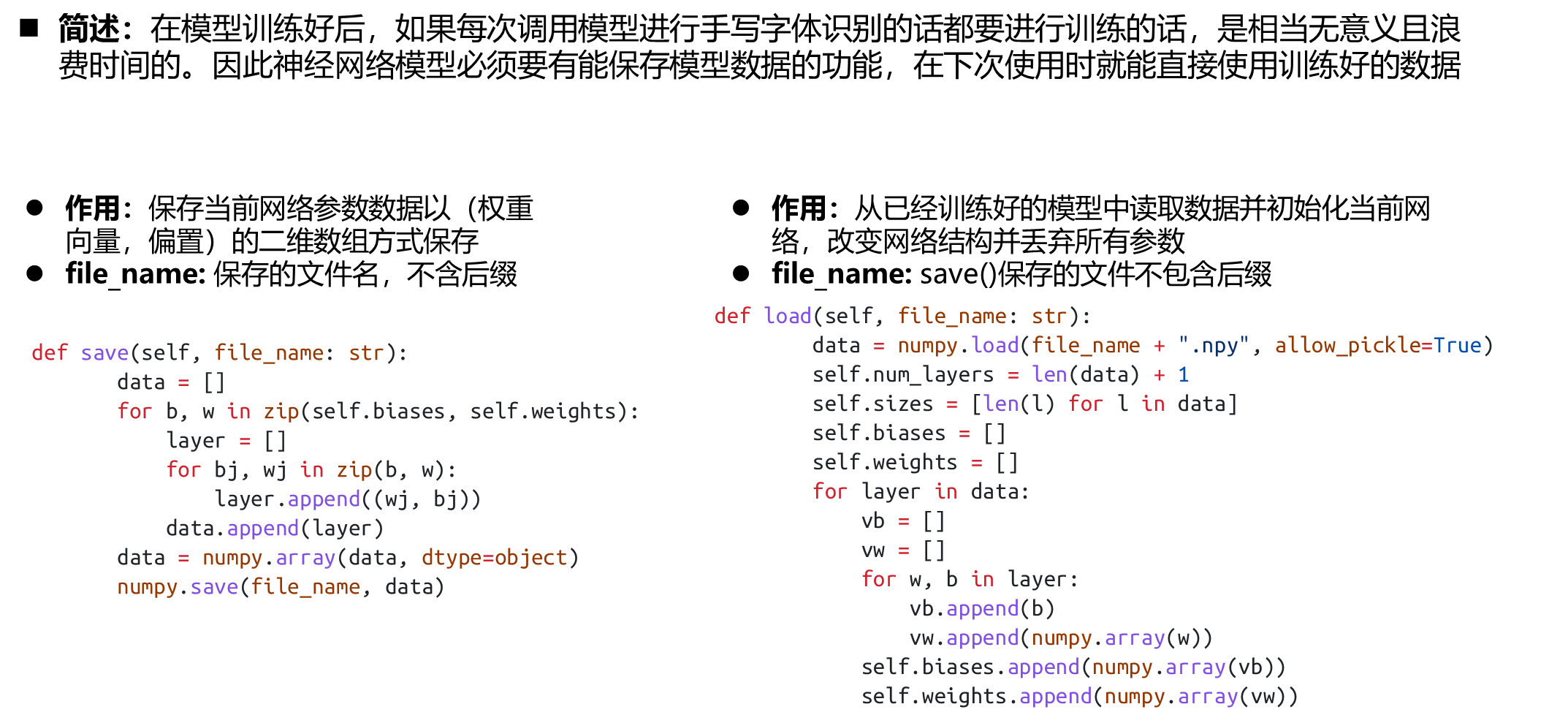
附录–全代码

哎呀，不想对着上面的流程一个个敲代码？我懂，我懂，所以这里直接给出全部代码的汇总，方便读者一键复制粘贴哟😈😈

import numpy


# 将输出压缩成激活值得函数
def sigmoid(z):
    return 1 / (1 + numpy.exp(-z))


# sigmoid 的导函数
def sigmoid_prime(z):
    return sigmoid(z) * (1 - sigmoid(z))


class Network(object):
    def __init__(self, sizes):
        self.num_layers = len(sizes)  # 网络中包含的层数（包括并不存在的输入层）
        self.sizes = sizes[1:]  # 各层网络节点数（不包含不存在的输入层）
        # 第一层为输入层，没有权重和偏执
        self.biases = [numpy.random.randn(y) for y in sizes[1:]]  # 二维数组：self.biases[i][j] 为第i+2层、第j+1个节点的偏置
        self.weights = [numpy.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]
        print("test,hahaha")
        # 权重为三维数组：self.weights[i][j] 为第i+2层、第j+1个节点的权重向量，向量维度为前一层的输出向量维度

    def save(self, file_name: str):
        """
        保存当前网络参数数据：以（权重向量，偏置）的二维数组方式保存
        :param file_name: 保存的文件名，不含后缀
        :return: None
        """
        data = []
        for b, w in zip(self.biases, self.weights):
            layer = []
            for bj, wj in zip(b, w):
                layer.append((wj, bj))
            data.append(layer)
        data = numpy.array(data, dtype=object)
        numpy.save(file_name, data)

    def load(self, file_name: str):
        """
        从文件中读取数据并初始化当前网络，改变网络结构并丢弃所有参数
        :param file_name: save()保存的文件不包含后缀
        :return:None
        """
        data = numpy.load(file_name + ".npy", allow_pickle=True)
        self.num_layers = len(data) + 1
        self.sizes = [len(l) for l in data]
        self.biases = []
        self.weights = []
        for layer in data:
            vb = []
            vw = []
            for w, b in layer:
                vb.append(b)
                vw.append(numpy.array(w))
            self.biases.append(numpy.array(vb))
            self.weights.append(numpy.array(vw))

    def feedforward(self, a):
        """
        :param a: 输入值：一个向量
        :return: 网络输出值：向量
        """
        for b, w in zip(self.biases, self.weights):  # 遍历所有层
            # b w 为[...]
            a = sigmoid(numpy.dot(w, a) + b)  # 计算当前层的激活数值向量，隐式的包含一个循环：遍历当前层的节点
        return a

    @staticmethod
    def cost_derivative(output_activation, y):
        """
        根据方程 (1) 计算输出层的误差：
        :param output_activation: 网络的实际输出，是一个十维的向量，0-9 的激活值
        :param y: 预期输出：在这里是一个整数值：0-9
        :return: 返回一个代表差异的向量，分别表示输出层各个节点的误差，正值表示比期望大，负值表示比期望小，
                 绝对值表示偏离期望的程度（修改的优先级）

        此处采用二次代价：
        对于单个样本：
        二次代价 C_x = \frac{(y-a)^2}{2}
                a = \sigma(z)
                \delta^L= a - y
        """
        # 由于期望输出向量是[0,0,0,0,0,0,0,0,0,0][y]=1,
        # 这里避免额外的向量计算，直接计算 output_activation - 期望输出向量
        output_activation = output_activation[:]
        output_activation[y] -= 1
        return output_activation

    # 计算梯度
    def backprop(self, x, y):
        """
        反向传播计算梯度
        :param x: 单个输入
        :param y: 期望输出
        :return: 梯度
        """
        # 这里构造一个存储权重 和 偏置 改变量（梯度）的容器，初始化为0
        nabla_b = [numpy.zeros(b.shape) for b in self.biases]
        nabla_w = [numpy.zeros(w.shape) for w in self.weights]
        activation = x  # 当前层输入的激活向量
        activations = [numpy.array(x)]  # 保存压缩后的激活值 （x 为输入层的激活值）
        zs = []  # 保存每一层的输出（未压缩）

        # 这里模拟一个前向传播的过程，将每一层的输出（未压缩）保存在zs中，压缩后的激活值（作为下一层的输入）保存在activations
        for b, w in zip(self.biases, self.weights):
            z = numpy.dot(w, activation) + b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)

        # 反向传播核心算法
        """
        反向传播：
        cost_derivative()计算输出层的梯度，对应输出层各个节点输出值的误差，
        为减少各个节点误差：（误差为正表示输出应当减小，反之增加，以下说明以误差为正值为前提）
            1.调整权重：减小该节点所有正输入对应权重，增加所有负输入对应权重
            2.减小偏置
            3.调整上一层的输出：减少正权重对应输出，增加负权重对应输出（反向传递）
        此外：不同误差表示调整该节点的性价比，误差很小意味着该节点输出很接近期望，即没必要调整，反之则意味着调整的性价比很高
             相应计算出的对应梯度绝对值大小表示调整的性价比
        """
        # 核心方程 README.md
        delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(
            zs[-1]
        )  # 根据方程 (1) 计算输出层误差向量

        nabla_b[-1] = delta  # 根据方程(3) 误差向量即偏置的梯度
        # 根据方程 (4) 计算输出层权重梯度
        # reshape()是为了将向量转化为矩阵(只有二维向量支持矩阵运算)(单行或单列)，做矩阵乘法
        nabla_w[-1] = numpy.dot(
            delta.reshape(self.sizes[-1], 1),
            activations[-2].reshape(1, len(activations[-2])),
        )
        # 输出层梯度计算完毕，这里从倒数第二层反向计算所有层梯度（不包含输入层）
        for l in range(2, self.num_layers):
            z = zs[-l]
            delta = numpy.dot(self.weights[-l + 1].transpose(), delta) * sigmoid_prime(
                z
            )  # -l 层误差计算使用方程 (2) 由下一层表示当前层
            # 原理与计算输出层相同
            nabla_b[-l] = delta
            # 方程 (4)
            nabla_w[-l] = numpy.dot(
                delta.reshape(len(delta), 1),
                activations[-l - 1].reshape(1, len(activations[-l - 1])),
            )
        return nabla_b, nabla_w

    def update_mini_batch(self, mini_batch, eta):
        """
        根据小批量数据计算梯度更新权重和偏置，以减小误差
        :param mini_batch: 小批量数据，包含若干个 (x, y) 组合，x 为输入，y 为期望输出
        :param eta: 学习速率，每次更新会乘这个系数，值越大，则更改的越大
        :return: None
        """
        # 拷贝权重和偏置，填充为 0
        nabla_b = [numpy.zeros(b.shape) for b in self.biases]
        nabla_w = [numpy.zeros(w.shape) for w in self.weights]
        # 遍历样本中所有数据
        for x, y in mini_batch:
            # 计算得到权重和偏置的梯度
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            # 将所有样本中的梯度求和（相当于取平均值，但没有除以样本大小，变相增加学习速率）
            nabla_b = [nb + dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [
            w - (eta / len(mini_batch)) * nw for w, nw in zip(self.weights, nabla_w)
        ]
        self.biases = [
            b - (eta / len(mini_batch)) * nb for b, nb in zip(self.biases, nabla_b)
        ]

    def evaluate(self, test_data):
        """
        评估当前神经网络，返回判断正确的样本数
        :param test_data: 用于评估的数据集
        :return: 数据集中判断正确的样本数量
        """
        test_result = [(numpy.argmax(self.feedforward(x)), y) for x, y in test_data]
        return sum(int(x == y) for x, y in test_result)

    def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None):
        """
        加载训练数据集对网络进行训练，可接受测试数据集评估每一个周期的效果，但这会消耗更多时间
        :param training_data: 一个（x,y）元组的列表，x 表示输入，y 表示期望的输出
        :param epochs:   训练的周期
        :param mini_batch_size:  小批量训练数据大小
        :param eta: 学习速率
        :param test_data: 测试数据集，给出该数据会在每个周期打印评估结果，这会拖慢学习速度
        :return: None
        """
        # if test_data != None:
        n_test = len(test_data)

        n = len(training_data)  # n:测试数据集的大小
        for j in range(epochs):
            # 打乱训练数据
            numpy.random.shuffle(training_data)
            # 将训练数据分割成多个指定大小的小批量数据
            mini_batches = [
                training_data[k : k + mini_batch_size]
                for k in range(0, n, mini_batch_size)
            ]
            for mini_batch in mini_batches:
                # 小批量数据学习
                self.update_mini_batch(mini_batch, eta)
            # 打印进展
            if test_data != None:
                num = self.evaluate(test_data)
                print(
                    "周期:{0}  {1}/{2} {3}%".format(
                        j + 1, num, n_test, num / n_test * 100
                    )
                )
            else:
                print("周期 {0}  完成！".format(j + 1))


if __name__ == "__main__":
    # 加载数据
    training_data = numpy.load("training_data.npy", allow_pickle=True)
    test_data = numpy.load("test_data.npy", allow_pickle=True)
    validation_data = numpy.load("validation_data.npy", allow_pickle=True)
    # 创建神经网络
    net = Network([784, 15, 10])  # 输入层784 输出层10 固定，其他层可以任意
    # 加载训练数据训练
    net.SGD(
        training_data, 5, 5, 1, test_data
    )  # 参数依次为：训练数据集、训练周期、小批量数据大小、学习速率（省略了测试数据集）

    # 加载验证数据集对网络效果进行验证
    n_validation = len(validation_data)  # 获得验证数据集大小
    num = net.evaluate(validation_data)  # 获得评估正确样本数
    # 打印结果
    print("验证：{0}/{1} {2}%".format(num, n_validation, num / n_validation * 100))

参考文献

本文的理论部分大多数都参考了邱锡鹏老师所著的《Neural Network and Deep Learning
https://nndl.github.io/
有兴趣的同学也可以去看看这本书，难度较大，但是干货满满