论文网址：M₂DC: A Meta-Learning Framework for Generalizable Diagnostic Classification of Major Depressive Disorder | IEEE Journals & Magazine | IEEE Xplore

目录

1. 心得

2. 论文逐段精读

2.1. Abstract

2.2. Introduction

2.3. Related Works

2.3.1. Domain Generalization

2.3.2. Meta-Learning

2.3.3. Graph Neural Network on Brain Graphs

2.4. Methods

2.4.1. Problem Definition

2.4.2. Meta-Learning With Distance Constraint

2.4.3. Meta Batch Normalization

2.4.4. Meta-Learning With MetaBN and Distance Constraint

2.4.5. Concatenated SpatioTemporal Attention Graph Isomorphism Network

2.5. Experiment

2.5.1. Datasets and Preprocessing

2.5.2. Implement Details and Setup

2.5.3. Comparisons Between Different Graph Isomorphism Networks

2.5.4. Comparisons With Other Methods

2.5.5. Ablation Study

2.5.6. Comparison With State-Of-The-Art Studies

2.5.7. Control Analysis of Hyper-Parameters

2.5.8. Discriminative Brain Regions

2.6. Discussion

2.7. Conclusion

1. 心得

（1）我要开始走简易科普路线了，中文不能看不懂了吧

2. 论文逐段精读

2.1. Abstract

        ①现存问题：扫描机或参数存在差异

2.2. Introduction

        ①对于不同参数和扫描机下的数据，作者提出了一个域泛化模型

2.3. Related Works

2.3.1. Domain Generalization

        ①介绍一些域泛化的模型

2.3.2. Meta-Learning

        ①参考了MLDG和MetaBN

2.3.3. Graph Neural Network on Brain Graphs

        ①介绍一些模型，并提到参考STAGIN

2.4. Methods

2.4.1. Problem Definition

        ①构建个滑窗的脑图：

其中每个图由节点和边缘构成，比如这是第个滑窗的图：

对于每个图如图节点有 个，是脑区个数：

边缘是每个节点间的：

这是遍历每个节点，但以节点举例，的邻居域是，是邻域的所有节点

        ②作者先训练一个参数是的神经网络把图特征变成嵌入：

再训练一个分类器把嵌入变成预测结果：

        ③作者可能意图训练集和测试集来源于不同站点或数据集，不过还是一样的疾病分类。因此源域和目标域在标签空间上没差别（，，就是都是正常人和MDD俩类别），但特征空间是不太一样的（，，不同医院可能设备不一样）。作者想用参数和来进行推理

2.4.2. Meta-Learning With Distance Constraint

        ①在源域中，设定个元训练域和个元测试域，先使用元训练域的交叉熵损失函数来更新梯度（在个元训练域中均分）：

其中是logit（就是分类概率），代表第个元训练域的脑图和标签

        ②用元训练域平均来的梯度更新模型参数：

其中是学习率，

        ③采用距离约束聚类相同标签，如果是同一标签就最小化欧氏距离，如果是不同标签就让距离大于：

其中，，，是欧几里得距离。约束图例：

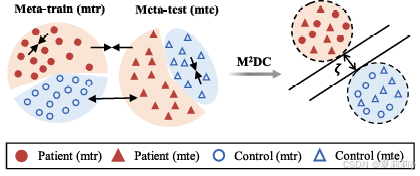
        ④元测试（是源域的测试集）阶段的总损失函数：

        ⑤怎么Adam优化器都写出来了：

        ⑥算法：

2.4.3. Meta Batch Normalization

        ①在元测试阶段采样一个元训练阶段的分布：

其中是高斯分布，采类的个样本，一共个，特征是：

这个每一层都是批归一化的，要和元测试集混合（这就是作者的MetaBN，和普通BN是不一样的）：

其中是遵循 Beta 分布的混合系数，。（作者会在下一节提到，是显得有点混乱）

        ②元训练集和元测试集特征混合完再批归一化一下：

2.4.4. Meta-Learning With MetaBN and Distance Constraint

        ①元训练阶段的分类损失：

（这个不是提过一遍了吗为什么又再提）

        ②元测试阶段损失：

（这个不是上面也有吗为什么要再提一遍？）

2.4.5. Concatenated SpatioTemporal Attention Graph Isomorphism Network

        ①网络架构：

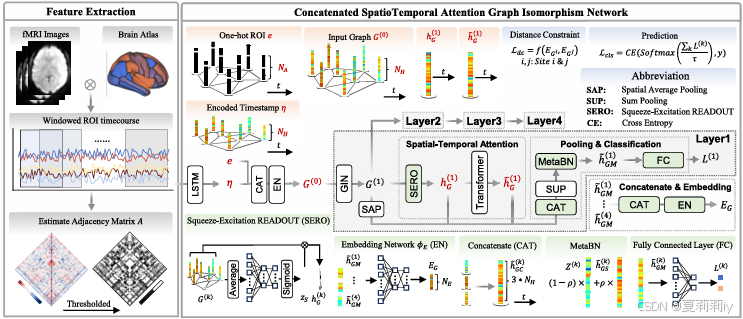
其中主干是CSTAGIN（这图怎么看着怪混乱的）

        ②图的节点特征是one hot编码加上时间戳，它会经过线性层来提取特征：

其中，是隐藏层维度，

        ③CSTAGIN：

是皮尔逊算的吧，阈值还不知道

        ④串联一切：

作为输出特征，其中是空间平均池化

        ⑤最终输出特征，再经过和池化和MetaBN：

这就是作者最早定义的嵌入，虽然不知道为什么要用这么有歧义的字母，像个函数似的，

2.5. Experiment

2.5.1. Datasets and Preprocessing

        ①REST-Meta-MDD数据集用了1300个中的1236MDD患者和1128中1081名健康人的数据，排除了站点5和1因为9它们没有提供计算连接组所需的时间过程

        ②用了中国五家医院的私有数据集：

AMU	安徽医科大学附属第一医院	103 名患者 vs. 94 名对照
FMMU	第四军医大学西京医院	60 名患者 vs. 50 名对照
SMU	山西医科大学第一医院	146 名患者 vs. 97 名对照
CSU#1	中南大学湘雅第二医院	179 名患者 vs. 123 名对照
CSU#2	中南大学湘雅第二医院	42 名患者 vs. 50 名对照

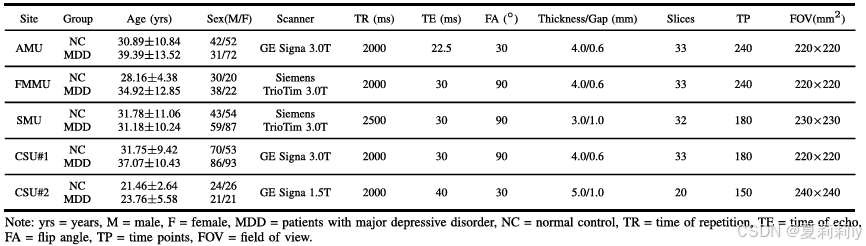
        ③用的脑图谱是AAL116和CC200，算FC是皮尔逊，阈值是前30%

2.5.2. Implement Details and Setup

        ①CSTAGIN网络骨干层数：4

        ②CSTAGIN隐藏维度为：

        ③：三层MLP，输出维度

        ④研究中内部验证、外部验证和训练范式的示意图：

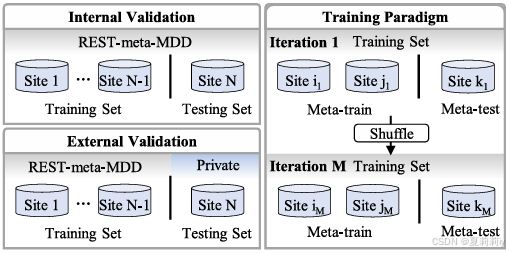
在内部验证中，训练集和测试集均来源于REST-meta-MDD项目。在外部验证中，训练集来自REST-meta-MDD项目，测试集则来自私有数据集。在训练过程中，来自两个源站点的大脑图像被随机选取作为meta-train数据集，而来自另一个源站点的大脑图像则被选为meta-test数据集。在每次迭代前，所有源站点都会被随机打乱顺序，然后随机选择meta-train和meta-test数据集。

        ⑤重复实验次数：6

        ⑥和的初始学习率：，在第 10、25、40 和 50 纪元分别除以 10

        ⑦的学习率：

        ⑧超参数：

2.5.3. Comparisons Between Different Graph Isomorphism Networks

        ①模型在不同内部目标测试站点上的结果：

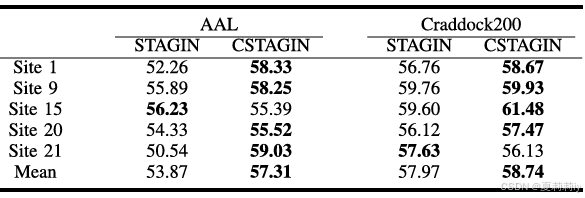
2.5.4. Comparisons With Other Methods

        ①内部比较：

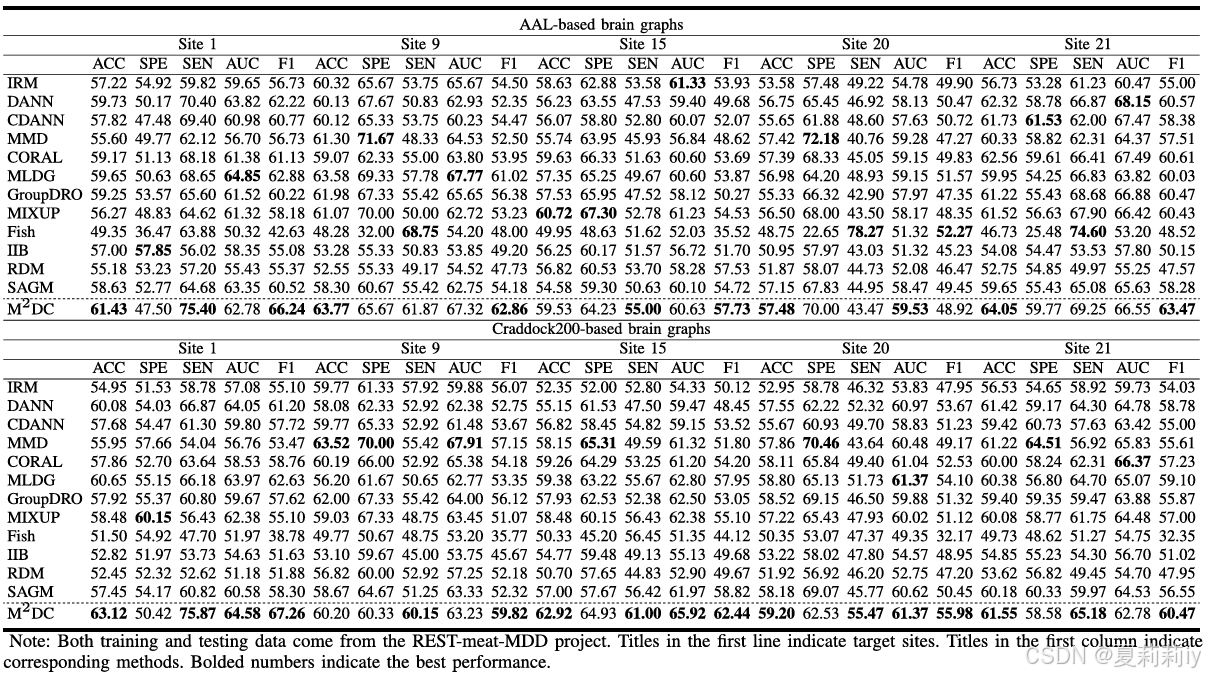
        ②外部比较：

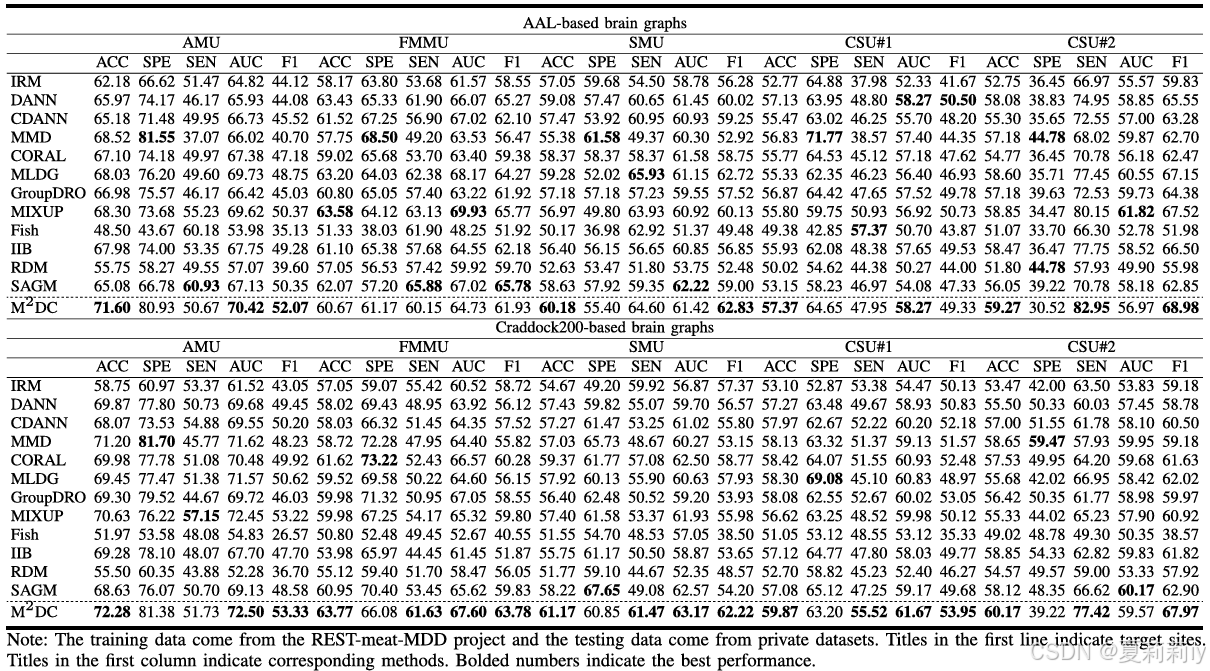
        ③不同脑模板下内部和外部平均性能：

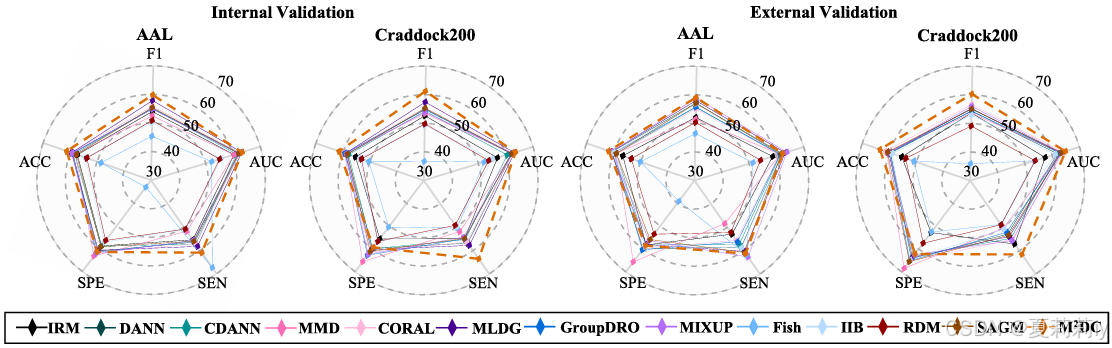
2.5.5. Ablation Study

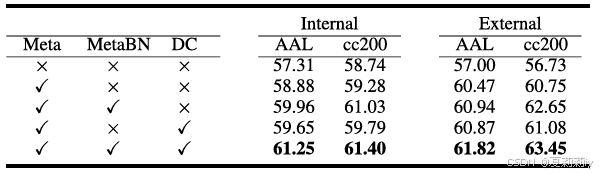
        ①消融研究：

        ②t-SNE对比：

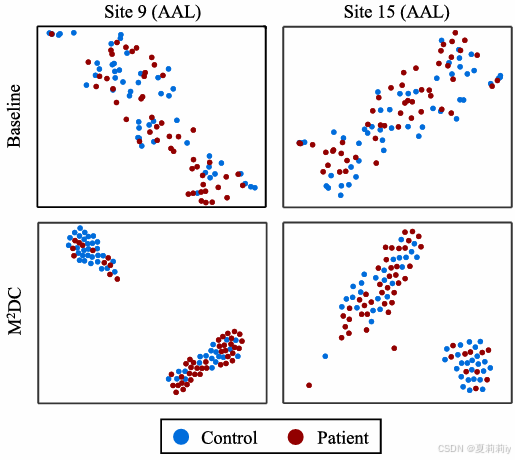
（咦？？我没看明白呢，怎么没咋分开，是因为性能本身就不好吗）

2.5.6. Comparison With State-Of-The-Art Studies

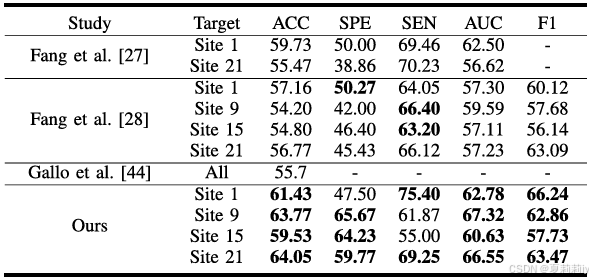
        ①和SOTA的比较：

2.5.7. Control Analysis of Hyper-Parameters

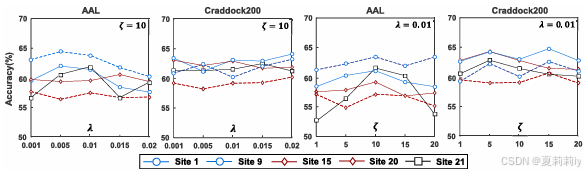
        ①超参数实验：

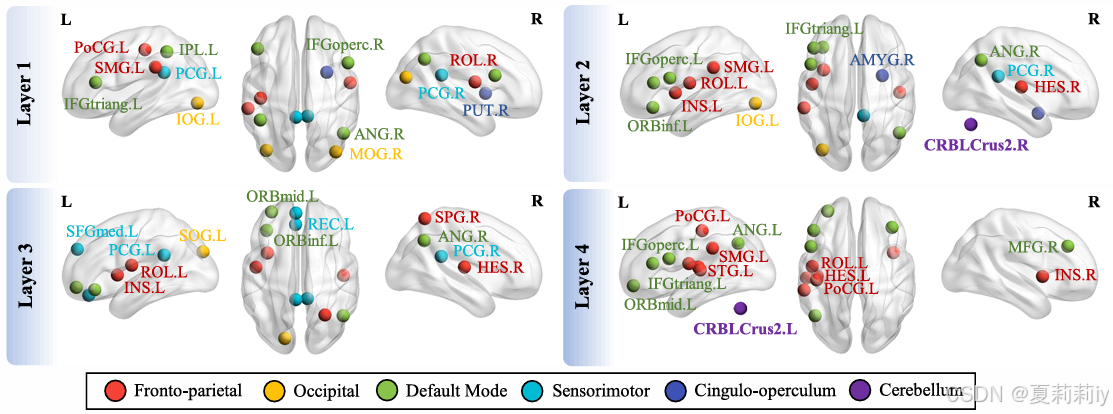
2.5.8. Discriminative Brain Regions

        ①显著脑区：

2.6. Discussion

        ①对来自私有数据集的成像数据应用了与 REST-meta-MDD 项目相同的预处理管道，因此对不同处理是否同时有效泛化未知

2.7. Conclusion

        ~